
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовая последовательность.Содержание книги Поиск на нашем сайте
Цели Знать: v Определение функции, её области определения и области значений; v способы задания функций; v основные характеристики функции; v понятие обратной функции; v понятие сложной функции. Уметь: v Строить графики основных элементарных функций.
▼ Пусть даны два непустых множества X и Y. Соответствие f, которое каждому элементу y=f(x) или Множество Х называется областью определения функции f и обозначается D (f). Множество всех
Основные характеристики функции 1. Функция у=f (x), определённая на множестве D, называется · чётной, если · нечётной, если Фцнкция у=f (x), определённая на множестве D, не являющаяся ни четной, ни нечётной называется функцией общего вида. Пример. Чётные функции: f (x) =x 2 n, y=cos x. Нечётные функции: f (x) =x 2 n – 1, y=sin x. 2. Пусть функция у=f (x), определёна на множестве D и пусть · f (x 1) <f (x 2), то функция называется возрастающей на множестве D 1 (4); · · f (x 1) >f (x 2), то функция называется убывающей на множестве D 1 (6); · 3. Функцию у=f (x), определённую на множестве D, называют ограниченной на этом множестве, если существует такое число M >0, что для всех
4. Функция у=f (x), определённая на множестве D, называется периодической на этом множестве, если существует такое число T >0, что при каждом f (x+T) =f (x) (9). Пример. Функции у=sin x, у=cos x имеют период Функция φ (у) называется обратной к функции f (x), если для всякого x=φ (y) =f - – 1(y) (10).
Основные элементарные функции 1) степенная функция
2) показательная функция у=ах (а >0, a 3) логарифмическая функция y= log ax (a >0, a 4) тригонометрические функции y= sin x, y= cos x, y= tg x, y= ctg x; 5) обратные тригонометрические функции y= arcsin x, y= arcos x, y= arctg x, y= arcctg x.
▼ Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией. ▲ ▼ Пусть функция y=f (u) определена на множестве D, а функция u = φ (х) на множестве D 1, причём Пример. y= sin(lg x); y= tg(3 x +1).
№1. Дана функция ► №2. Найти область определения функции: а) ► а) Функция принимает действительные значения в тех точках, в которых выражение, стоящее под знаком корня, будет иметь неотрицательные значения, а выражение, находящееся под знаком логарифма — положительным:
Решая первое неравенство Решая второе неравенство Решение системы: б) Функция Функция arcсos
откуда Таким образом, данная функция определена на отрезке [ –1; 3]. ◄
№3. Выяснить, какие из данных функций, являются чётными и какие нечётными: а) в) q (x)= x +sin x. ► Заменяя х на (– х), получаем: а) отсюда следует, что f (– x)= f (x), т.е. функция чётная; б) g (– x)= – x +cos(– x)= – x +cos x, отсюда g (– x) в) q (– x)= – x +sin x = – x – sin x, отсюда q (– x)= – q (x), т.е. функция чётная. ◄
Задания для самостоятельного решения №1. Дана функция f (t)=2 t 3 – 3 t +4. Найти f (–2); f (0); f (1); f (a). Ответ: f (–2)= –6; f (0)= 4; f (1)=3; f (a)=2 a 3 – 3 a +4. №2. Дана функция, Ответ: Функция не определена в точках №3. Дана функция f (x)=sin x. Найти:1) f 2(x)+ 2) Ответ: 1) 1; 2) tg x; 3) sin 2 x; 4) sin 1; 5) sin(–2). №4. Найти области определения функции: 1) y =lg(4 – 3 x – x 2); 2) Ответ: 1) D (y)=(–4; 1); 2) D (y)= R \{ –2; 7};
3) D (y)=[ –1; 2]; 4) D (y)= R \{ 5) D (y)=Æ; 6) D (y)= 8) D (y)=[1; 3) 10) D (y)= 11) D (y)= №5. Найти множество значений функции: 1) 4) y =3+2 x – x 2, –1 Ответ: 1) 3) [1; 2]; 4) [ –12; 0]; 5) №6. Какие из указанных функций чётные, какие нечётные и какие из них не обладают этими свойствами: 1) у =5 х; 2) y = x 2 3 x; 3) y = x – x 3; 4) y = x 2+3 x +2; 5) у = x 3+2 x +1; 6) y =sin2 x; 7) Ответ: Функции 6, 9, 10 — чётные; функции 3, 8 — нечётные; функции 1, 2, 4, 5, 7 — общего вида. №7. Записать сложную функцию у = у (u (v (x))), где: 1) y =sin u; u =lg v; v = Ответ: 1) y =sin(lg №8. Сложную функцию у записать в виде цепочки равенств: 1) у =(2 х – 5)10; 2) y =lg Ответ: 1) y = u 10; u =2 x – 5; 2) y =lg v; v =tg w; w = Занятие 2 Цели Знать: v Определение последовательности; бесконечно малой и бесконечно большой последовательности; v определение предела числовой последовательности; v основные свойства и операции над пределами последовательностей. Уметь: v Вычислять предел последовательности, используя основные свойства и операции над пределами последовательностей.
Под числовой последовательностью х 1, х 2, х 3, …, хn, … понимается функция xn=f (n), (11) заданная на множестве натуральных чисел.
Пример. Если известен общий член последовательности xn = Предел функции. Раскрытие неопределённостей вида Цели Знать: v Определение предела; v признаки существования пределов; v основные теоремы о пределах. Уметь: v Применять основные теоремы о пределах; v применять признаки существования пределов при вычислении предела функции; v вычислять пределы, раскрывая неопределённости вида
Определение («на языке последовательностей», или по Гейне) Число А называется пределом функции y=f (x)в точке х 0 (или при
Определение (на «языке ε-δ», или по Коши») Число А называется пределом функции y=f (x)в точке х 0 (или при Основные теоремы о пределах Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Следствие. Функция может иметь только один предел при Теорема 2. Предел произведения двух функций равен произведению их пределов:
Теоремы 1 и 2 справедливы для любого конечного числа функций. Следствие. Постоянный множитель можно выносить за знак предела:
Следствие. Предел степени с натуральным показателем равен той же степени предела:
Следствие. Теорема. Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
При нахождении пределов применяют соотношения:
(28).
Постановка задачи. Найти План решения. Для того чтобы найти
№9. Найти пределы: 1) 3) ► 1) Применяя теоремы о пределах, получаем:
= 2) Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, находим: 3) Непосредственно применять теорему о пределе частного нельзя, так как предел знаменателя равен нулю (в знаменателе есть бесконечно малая величина при
Постановка задачи. Найти План решения. Для того чтобы найти Неопределённость вида
· Чтобы раскрыть неопределённость Неопределённость вида
Частный случай: предел рационального выражения вида
№10. Найти пределы: 1) 2) ► 1)
сократим множитель (х – 3) имеем:
2)
В числителе последнего выражения получилась формула — разность квадратов, таким образом:
3)
тогда исходное пределное выражение имеетвид:
которое раскрывается по известным правилам, т.е.:
№11. Найти пределы: 1) 3) ► 1)
2)
3)
4)
№12. Найти пределы: 1) 2) ► Данные предельные соотношения можно рссмотреть, как частное двух многочленов, т.е: 1) 2) 3)
Постановка задачи. Найти План решения. Для того чтобы найти
№13. Найти пределы: 1) ► 1)
2) Рассмотрим два случая: а)
= б)
Аудиторные задания Найти пределы: №51 №52 №53. №54. №55. №56. №57. №58. №59. №60. №61. №62. №63. №64. №65. №66. №67. №68. №69.
Домашние задания Найти пределы: №70. №71. №72. №73. №74. №75. №76. №77. №78. №79. №80. №81. №82. №83. №84. №85. №86. №87. №88. №89. №90. №91. №92. №93.
Дополнительные задания Найти пределы: №94. №95. №96. №97. №98. №99. №100. №101. №102. №103. №104. №105. №106. №107. №108. №109. №110. №11 №112. №113. №114. №115. №116. №117. №118. №119. №120. №121. №122.
Занятие 4 Замечательные пределы Цели Знать: v Замечательные пределы и их следствия. Уметь: v Вычислять пределы, используя замечательные пределы.
Первый замечательный предел
Следствия
Второй замечательный предел
где е Следствия
Постановка задачи. Найти План решения. Для того чтобы найти данный предел следует вычислить 1) если существуют конечные пределы 2) если
3) если
№14. Найти пределы:1) 3) 6) ► 1)
2) | ||||||
|
| Поделиться: |

 сопоставляет один и только один элемент
сопоставляет один и только один элемент  , называется функцией и записывается
, называется функцией и записывается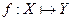 (1). ▲
(1). ▲ выполняются условия
выполняются условия  и f (–x) =f (x) (2);
и f (–x) =f (x) (2); и f (–x)= – f (x) (3).
и f (–x)= – f (x) (3). . Если для любых значений
. Если для любых значений  аргументов из неравенства x 1 <x 2 вытекает неравенство:
аргументов из неравенства x 1 <x 2 вытекает неравенство: , то функция называется неубывающей на множестве D 1 (5);
, то функция называется неубывающей на множестве D 1 (5); , то функция называется невозрастающей на множестве D 1 (7).
, то функция называется невозрастающей на множестве D 1 (7).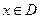 выполняется неравенство:
выполняется неравенство: (8).
(8). и
и , у=tg x, у=ctg x имеют период
, у=tg x, у=ctg x имеют период  .
. (
( );
); 1);
1); соответствующее значение u = φ (х)
соответствующее значение u = φ (х)  . Тогда на множестве D 1 определена функция u=f (φ (х)) которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции). Переменную u = φ (х) называют промежуточным аргументом сложной функции. ▲
. Тогда на множестве D 1 определена функция u=f (φ (х)) которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции). Переменную u = φ (х) называют промежуточным аргументом сложной функции. ▲ Найти f (–2); f (0).
Найти f (–2); f (0). ;
;  . ◄
. ◄ ; б) y =
; б) y =  +arcсos
+arcсos  .
.
 , имеем
, имеем 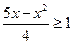 или х 2 – 5 х +4
или х 2 – 5 х +4  , т.е.
, т.е.  .
. , имеем 5 x – x 2>0, т.е.
, имеем 5 x – x 2>0, т.е.  .
. 0 или
0 или  .
. или
или 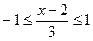
 или
или 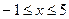 .
. ; б) g (x)= x +cos x;
; б) g (x)= x +cos x; =
=  =
=  ,
, . Найти
. Найти  ;
;  . В каких точках функция не определена?
. В каких точках функция не определена? ;
; 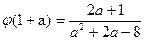 .
. .
. ;
; ; 3)
; 3) 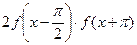 ; 4) f (1); 5) f (–2).
; 4) f (1); 5) f (–2). ; 3)
; 3) 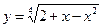 ; 4)
; 4)  ; 5)
; 5)  ; 6) y =arcсos
; 6) y =arcсos  ; 7) y =
; 7) y =  +lg(sin x); 8) y =log2(x 2 – 7 x +12)+
+lg(sin x); 8) y =log2(x 2 – 7 x +12)+ 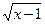 ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12) y =lg(sin x +2).
; 12) y =lg(sin x +2).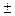 4};
4};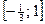 ; 7) D (y)=[ –5; –
; 7) D (y)=[ –5; –  )
)  (0;
(0;  ); 9) D (y)=
); 9) D (y)= 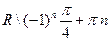 ,
,  ;
; ,
,  ,
, 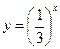 ,
, 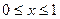 ; 2)
; 2)  , –1< x <0; 3) y =lg x, 10
, –1< x <0; 3) y =lg x, 10  ;
; 5; 5) y =cos x,
5; 5) y =cos x, 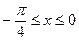 .
. ; 2) (–
; 2) (–  .
.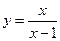 ; 8) y =
; 8) y =  ; 9) у = x 4+ x 2 – 5; 10) f (x) =const.
; 9) у = x 4+ x 2 – 5; 10) f (x) =const. ; 2) y =arctg u; u =
; 2) y =arctg u; u = 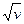 ; v =lg x.
; v =lg x. ).
). .
. .
. , то соответствующая последовательность будет: 1,
, то соответствующая последовательность будет: 1,  ,
,  ,
,  , …,
, …,  ,
, 
 ,
,  .
. ), если для любой последовательности допустимых значений аргумента xn,
), если для любой последовательности допустимых значений аргумента xn,  , сходящейся к х 0 (т.е.
, сходящейся к х 0 (т.е.  ), последовательность соответствующих значений функции f (xn),
), последовательность соответствующих значений функции f (xn),  ).
). ), если для любого положительно ε найдётся такое положительное число δ, что при всех
), если для любого положительно ε найдётся такое положительное число δ, что при всех 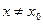 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. (22).
(22). (23).
(23). (24).
(24).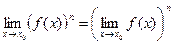 (25).
(25).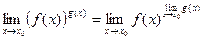 (26).
(26). , (
, ( ) (27).
) (27). , (k =const);
, (k =const);  ;
; ;
;  ;
; ;
; 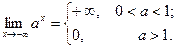
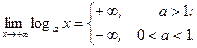 ;
; 
 .
. ; 2)
; 2)  ;
; .
. =
=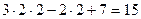 ;
; ;
; ). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины
). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины  , отличной от нуля, на бесконечно большую величину
, отличной от нуля, на бесконечно большую величину 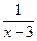 при
при  . ◄
. ◄ или
или  .
. и сокращаем на него, т.к.
и сокращаем на него, т.к.  .
. при
при  будем рассматривать как предел частного двух многочленов, который равен:
будем рассматривать как предел частного двух многочленов, который равен:
 ;
; ; 3)
; 3)  .
. , для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:
, для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители: ,
, =
=  ;
; . Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на
. Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на 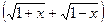 , тогда:
, тогда: .
. ;
;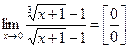 , для раскрытия данной неопределенности сделаем замену:
, для раскрытия данной неопределенности сделаем замену: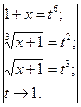
 ,
,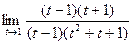 =
=  . ◄
. ◄ ; 2)
; 2)  ;
; ; 4)
; 4)  .
. , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда: =
=  ;
; , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда: ;
; , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда:
, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда: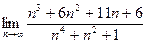 =
=  =
=  ;
; =
= 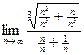 =
=  =0. ◄
=0. ◄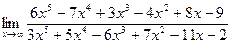 ;
; ; 3)
; 3)  .
. =
=  =2;
=2; ;
; .◄
.◄ ,
,  или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости
или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости  ; 2)
; 2)  .
.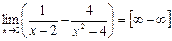 , данное предельное выражение преобразум таким образом:
, данное предельное выражение преобразум таким образом: =
=  ;
; . Перенеся иррациональность из числителя в знаменатель, получим:
. Перенеся иррациональность из числителя в знаменатель, получим: =
=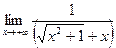 =0;
=0; . ◄
. ◄ . Ответ: 5.
. Ответ: 5. . Ответ:
. Ответ:  .
. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  .
. . Ответ: 2.
. Ответ: 2. . Ответ: –
. Ответ: –  .
. . Ответ:
. Ответ:  .
.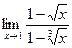 . Указание: замена: x = t 6. Ответ:
. Указание: замена: x = t 6. Ответ:  .
. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ: –9.
. Ответ: –9. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ: 4.
. Ответ: 4. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.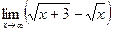 . Ответ: 0.
. Ответ: 0. . Ответ: 40.
. Ответ: 40. . Ответ:
. Ответ:  .
. . Ответ: 4.
. Ответ: 4. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ:
. Ответ:  .
.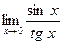 . Ответ:1.
. Ответ:1. . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ:  . Ответ:
. Ответ: 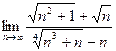 . Ответ: –1.
. Ответ: –1. . Указание: замена х +11= t 4. Ответ:
. Указание: замена х +11= t 4. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ: 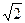 .
. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1.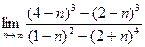 . Ответ: 0.
. Ответ: 0. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ: 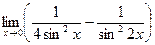 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  .
. . Ответ: –1.
. Ответ: –1. . Ответ: 2.
. Ответ: 2. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ: 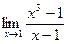 . Ответ: 3.
. Ответ: 3. . Ответ:
. Ответ:  .
.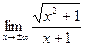 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ: 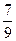 .
. . Ответ:
. Ответ: 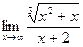 . Ответ: 0.
. Ответ: 0. . Ответ:
. Ответ:  . Ответ: 5.
. Ответ: 5. . Ответ:
. Ответ:  . Ответ: 1.
. Ответ: 1. . Ответ: 1.
. Ответ: 1. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ: 1.
. Ответ: 1. (29).
(29). ,
, ,
,  ,
, ,
,  ,
, ,
,  .
. ,
,  , (30)
, (30)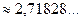 — число Эйлера.
— число Эйлера. ;
; ,
,  ;
;  ;
; ;
;  , (а =const).
, (а =const). .
. и
и  ;
; ;
;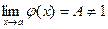 и
и  , то С находится с помощью формул:
, то С находится с помощью формул: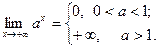

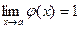 и
и  , где
, где  при
при  , получим:
, получим: =
=  .
. ; 2)
; 2)  ;
; ; 4)
; 4)  ; 5)
; 5)  ;
; ; 7)
; 7)  .
. . Воспользуемся первым замечательным пределом:
. Воспользуемся первым замечательным пределом: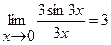 ;
;


