
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача нахождения затрат сырья, топлива и трудовых ресурсовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В таблице даны нормы затрат двух видов сырья и топлива на производство единицы продукции каждого цеха, трудоемкость в человеко-часах на единицу продукции, стоимость соответствующей единицы сырья и стоимость одного человеко-часа.
Найти: 1) Суммарные затраты сырья, топлива и трудовых ресурсов для выполнения программы производства; 2) полные затраты сырья, топлива и трудовых ресурсов каждым цехом и предприятием; 3) внутрипроизводственные затраты цехов. Решение. Заданная таблица непосредственно позволяет составить матрицу Д норм затрат сырья, топлива и трудовых ресурсов размера
и матрицу
1) Суммарные затраты сырья, топлива и трудовых ресурсов для выполнения программы предприятия получим путем умножения матрицы норм затрат Д на матрицу Х валового выпуска продукции:
Таким образом, для выполнения программы предприятия необходимо затратить: 1) сырья (а) – 1700 ед.; сырья (б) – 950 ед.; 2) топливо – 1650 ед.; 3) трудовых человеко-часов – 13000. 2) Затраты сырья, топлива и трудоемкости каждого цеха получим путем умножения нормы затрат каждого цеха на его валовый выпуск продукции:
Таким образом, матрица полных затрат сырья, топлива и трудовых ресурсов всего производства будет иметь вид:
3) Производственные затраты цехов получим умножением матрицы-строки стоимости
Таким образом, стоимость затрат первого цеха – 7200, второго – 11100, третьего – 44400.
Упражнения к главе 1 1. Вычислить определитель второго порядка
Ответ: 1) 7; 2) 0; 3) 0; 4) 0. 2. Решить уравнение
Ответ: 1) 4,5; 2) 7; 3) (-1; 2); 4) (2; -1). 3. Вычислить определители разложением по какой-нибудь строке или столбцу:
Ответ: 1) 14; 2) –14; 3) 27; 4) xyz. 4. Вычислить определители четвертого порядка: 1. Ответ: 1) 15; 2) –18; 3) 12; 4) –6. 5. Вычислить значение 1) 2) 3) 4) Ответы: 1) 3) 6. Транспонировать матрицы:
Ответы: 1). 7. Найти обратную матрицу к заданной матрице:
Ответы:
8. Найти ранг матрицы методом элементарных преобразований:
Ответы: 1) 2; 2) 3. 9. Решить системы уравнений методом Гаусса, по правилу Крамера, с помощью обратной матрицы: 1) 3) 5) Ответы: 1) 5) 10. Исследовать СЛАУ, для совместных систем найти общее и одно частное решение: 1) 3) Ответы: 1) Система совместна и определенна. Общее решение равно частному (1; 2). 2) Несовместна. 3) Совместна и неопределенна. О.р. 11. Найти общее решение и фундаментальную систему решений для однородной СЛАУ: 1) Ответы: 1) Общее решение (0; 0), фундаментальной системы решений нет. 2) 12. Найти фундаментальные системы решений однородных систем: 1) 3) Ответы: 1)
13. В таблице даны показатели потребности предложений трех отраслей промышленности (N – номер варианта):
а) Определить матрицу А потребностей-предложений; б) Через 5 лет потребности других отраслей возрастут до 24 + N, 33 + N и 75 + N на продукции отраслей 1, 2, 3 соответственно. Определить, сколько продукции должна произвести каждая отрасль, чтобы удовлетворить новые потребности. 14. Предприятие производит продукцию трех видов и использует сырье двух видов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей 1.6 Задания для индивидуальной семестровой работы студентов к главе 1 1. Решить систему линейных алгебраических уравнений: а) методом Крамера; б) методом Гаусса; с) матричным методом.
2. Найти фундаментальную систему решений и общее решение системы уравнений:
3. Предприятие выпускает три вида продукции с использованием трех видов сырья, характеристики производства указаны в таблице.
Найти объем выпуска продукции каждого вида при заданных запасах сырья. (N – номер варианта) Глава 2 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ Векторная алгебра Векторы и действия над ними Определение 1. Скалярными называются величины, которые характеризуются одним числом. Определение 2. Вектор – это направленный отрезок. Векторы обозначаются одной Определение 3. Длиной вектора называется его модуль и обозначается
где Направляющие косинусы вектора
Если известны координаты начала
Длина вектора
Определение 4. Вектор, длина которого равняется нулю, называется нулевым вектором. Определение 5. Вектор, длина которого равняется единице, называется единичным или ортом. Определение 6. Векторы, расположенные на одной или параллельных прямых, называются коллинеарными. Условие коллинеарности векторов
Определение 7. Векторы, расположенные на одной или параллельных плоскостях, называются компланарными. Определение 8. Два вектора называются равными, если они коллинеарны, сонаправлены и имеют одинаковые модули. Разность между координатами проекций конца и начала вектора
Если вектор Свойства проекций:
Произведение проекции вектора Нахождение проекции одного вектора на направление другого:
Определение 8. Линейными называются операции сложения, вычитания векторов и умножение вектора на число.
а) правило треугольника б) правило параллелограмма. Сложение векторов подчиняется обычным законам сложения – переместительному Разность векторов графически имеет вид:
Определение 9. Произведением вектора Произведение вектора на число обладает следующими свойствами:
Каждый вектор можно представить в виде произведения его модуля на орт. Пример 1. Даны начало Решение. Найдем координаты вектора
Пример 2. Даны векторы Решение. По формуле умножения вектора на число имеем:
По формуле сложения векторов имеем:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.178 (0.009 с.) |

 :
: ;
; стоимости сырья, топлива и трудовых человеко-часов:
стоимости сырья, топлива и трудовых человеко-часов: .
. .
. ;
;  ;
;  .
. .
. .
.


 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
. , если:
, если: .
. .
. .
. ,
, 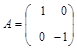 .
. . 2)
. 2)  .
. 4)
4) 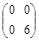 .
. .
.
 .
.
 . 2).
. 2).  .
. .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
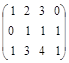 .
.
 .
.
 2)
2) 
 4)
4) 
 6)
6) 
 2)
2)  3)
3)  4)
4) 
 6)
6)  .
. 2)
2) 
 4)
4) 
 , ч.р. (3;0;0). 4) Совместна и неопределенна. О.р.
, ч.р. (3;0;0). 4) Совместна и неопределенна. О.р.  , ч.р. (0;0;1)
, ч.р. (0;0;1) 2)
2) 
 , (– 1; 1).
, (– 1; 1). 2)
2) 
 4)
4) 
 , 2)
, 2) 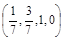 ,
,  , 3)
, 3)  ,
,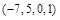 , 4)
, 4)  ,
,  .
. . Стоимость единицы сырья каждого типа заданы матрицей
. Стоимость единицы сырья каждого типа заданы матрицей  . Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 2000 единиц продукции второго вида и 150 единиц продукции третьего вида?
. Каковы общие затраты предприятия на производство 100 единиц продукции первого вида, 2000 единиц продукции второго вида и 150 единиц продукции третьего вида?








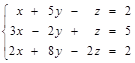
















































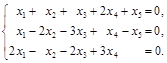
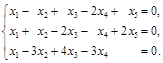
 ,
,  или двумя буквами
или двумя буквами  ,
, 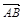 .
. или
или  :
: , (1)
, (1) – координаты вектора.
– координаты вектора. определяются по формулам:
определяются по формулам: . (2)
. (2) и конца
и конца  вектора, то координаты вектора
вектора, то координаты вектора 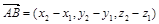 . (3)
. (3) . (4)
. (4) и
и  :
: .
. .
. , и проекция вектора положительна; если угол тупой, то проекция отрицательна; если вектор
, и проекция вектора положительна; если угол тупой, то проекция отрицательна; если вектор  ;
; ;
; .
. на ось l и единичного вектора этой оси называется составляющей вектора по оси l.
на ось l и единичного вектора этой оси называется составляющей вектора по оси l. .
. Сложение векторов графически имеет вид:
Сложение векторов графически имеет вид: и сочетательному
и сочетательному  .
.
 называется вектор
называется вектор  , коллинеарный вектору
, коллинеарный вектору  .
. ;
2).
;
2).  ;
3).
;
3). 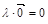
 ;
5).
;
5).  ;
6).
;
6). 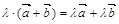 .
.
 и конец
и конец  вектора
вектора  или
или  .
. .
. и
и  . Найти координаты и длину вектора
. Найти координаты и длину вектора  .
. ,
, .
. .
.


