Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристическое уравнениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть х – собственный вектор квадратной матрицы А порядка п. Тогда имеет место матричное уравнение
где
Определитель системы однородных уравнений (4) называется характеристическим многочленом, а уравнение (5) – характеристическим уравнением матрицы А. Уравнение (5) имеет степень п относительно неизвестной Пример 2. Найти собственные числа и собственные векторы матрицы Решение. Характеристическое уравнение для этой матрицы имеет вид
Корни этого уравнения
По сути дела, это одно уравнение, поскольку определитель системы равен нулю. Полагая
которая через свободную переменную Поскольку Пример 3. Найти общее решение, частное решение и фундаментальную систему решений для СЛАУ:
Решение: Матрицы А и С имеют вид
Их ранги Выделим следующую подсистему
Считая
где Общее решение системы имеет вид
Частное решение системы получим, например, при
Давая свободным неизвестным поочередно значения, равные элементам столбцов определителя, порядка количества свободных неизвестных, в данном случае второго
получим векторы
представляющие собой фундаментальную систему решений. Общее решение теперь можно записать следующим образом:
Придавая коэффициентам
Примеры использования линейной алгебры в задачах экономического содержания Модель межотраслевого планирования потребностей и предложений Таблицей заданы показатели взаимных спросов и предложений между различными отраслями промышленности:
1) Найти матрицу потребностей–предложений А; 2) Допустим, что через 3 года потребности других отраслей возрастут до 26, 35 и 80 показателей для областей 1, 2, 3 соответственно. Сколько продукции должна произвести каждая отрасль, чтобы удовлетворить эти потребности? Решение. 1) Элементы искомой матрицы А равны отношению спроса i -ной отрасли к общему количеству предложений этой отрасли. Поэтому для нахождения элементов i- го столбца ( Таким образом, матрица потребностей–предложений:
2) Пусть Е – единичная матрица третьего порядка. Обозначим:
Х – матрица новых предложений, соответствующим новым потребностям.
Тогда:
Для вычисления будущих предложений осталось найти
Для вычисления матрицы
Обратная матрица
Подставив значение Д и найденную обратную матрицу
Таким образом, первой отрасли необходимо изготовить 130,9 единиц продукции, второй – 169,96, третьей – 219,87 единиц продукции через 3 года.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.48 (0.009 с.) |

 , или
, или  , (4)
, (4) – собственное значение матрицы А, а Е и
– собственное значение матрицы А, а Е и  – соответственно, единичная матрица и нулевой вектор-столбец. Поскольку собственный вектор не является нулевым, то однородная система (4) должна иметь ненулевое решение, т. е. в силу следствия 2 (см. ранее) определитель этой системы равен нулю:
– соответственно, единичная матрица и нулевой вектор-столбец. Поскольку собственный вектор не является нулевым, то однородная система (4) должна иметь ненулевое решение, т. е. в силу следствия 2 (см. ранее) определитель этой системы равен нулю: . (5)
. (5) .
.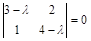 , откуда, раскрывая определитель, получаем:
, откуда, раскрывая определитель, получаем: .
. ,
, 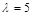 . Для нахождения собственных векторов подставим найденные собственные значения в систему однородных уравнений (4) при
. Для нахождения собственных векторов подставим найденные собственные значения в систему однородных уравнений (4) при 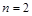 , соответствующей заданной матрице А. Собственный вектор, соответствующий собственному значению
, соответствующей заданной матрице А. Собственный вектор, соответствующий собственному значению  , является решением системы
, является решением системы
 свободной переменной, получаем первый собственный вектор
свободной переменной, получаем первый собственный вектор 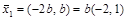 . Подстановка второго собственного значения
. Подстановка второго собственного значения 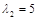 приводит к системе уравнений
приводит к системе уравнений
 определяет второй собственный вектор матрицы А:
определяет второй собственный вектор матрицы А:  .
. и с – произвольные числа, то одному собственному значению может соответствовать несколько собственных векторов разной длины. Например, собственные векторы, соответствующие фундаментальным решениям однородных систем (в данном случае их будет по одному на каждое собственное значение), имеют вид,
и с – произвольные числа, то одному собственному значению может соответствовать несколько собственных векторов разной длины. Например, собственные векторы, соответствующие фундаментальным решениям однородных систем (в данном случае их будет по одному на каждое собственное значение), имеют вид,  .
.
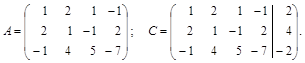
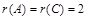 , значит, СЛАУ совместна.
, значит, СЛАУ совместна.
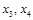 известными, ее решение найдем по формулам Крамера:
известными, ее решение найдем по формулам Крамера: ,
, .
. ,
,  :
: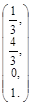 .
. ,
, ,
,
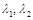 различные числовые значения, получим различные частные решения. Любое частное решение можно получить путем подходящего выбора коэффициентов
различные числовые значения, получим различные частные решения. Любое частное решение можно получить путем подходящего выбора коэффициентов 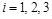 ) матрицы А необходимо разделить потребности i- й отрасли, указанной в таблице, на общее количество предложений этой отрасли.
) матрицы А необходимо разделить потребности i- й отрасли, указанной в таблице, на общее количество предложений этой отрасли.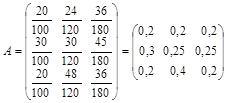 .
. – матрица–столбец новых потребностей.
– матрица–столбец новых потребностей. .
. . (1)
. (1)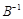 . Матрица
. Матрица  квадратная, третьего порядка, ее определитель:
квадратная, третьего порядка, ее определитель: .
.

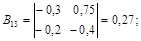



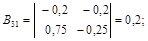


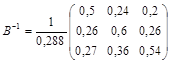 .
.