
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование несобственных интеграловСодержание книги
Поиск на нашем сайте
Исследование несобственных интегралов проводят путем использования предельного перехода к определенному интегралу. Интегралы с неограниченными пределами рассматривают так:
Определение 3. Если указанные пределы существуют (являются конечными числами), то соответствующий интеграл называется сходящимся и он равен своему пределу. Определение 4. Если какой-то предел не существует или равен бесконечности, то интеграл называется расходящимся. Пример 1. Вычислить интеграл Решение. Согласно определению несобственного интеграла имеем:
Итак, этот интеграл существует, сходящийся и равен 1. Пример 2. Вычислить интеграл Решение. В точке По определению такого несобственного интеграла имеем:
Итак, интеграл расходится. Пример 3. Вычислить несобственной интеграл или установить его сходимость. Решение.
Пример 4. Вычислить интеграл и установить его сходимость. Решение.
Применение определенных интегралов 4.3.1 Вычисление площадей плоских фигур Одним из важнейших применений определенного интеграла есть вычисления площадей. Рассмотрим несколько примеров. 1 Если на отрезке
можно найти площадь криволинейной трапеции, изображенной на рисунке.
2 Если
3 Если площадь
Пример 3. Вычислить площадь фигуры, ограниченной кривыми Решение. Для того, чтобы начертить рисунок, необходимо найти координаты точки пересечения кривых
Поскольку функции Тогда
4 Если криволинейная трапеция ограничена кривой, которая задается параметрически
Решение. Найдем
Таким образом, 5 Если кривая задается уравнением в полярных координатах
где
Пример 3. Вычислить площадь фигуры, ограниченной лемнискатой Бернулли Решение. Кривая симметрична относительно координатных осей, поэтому достаточно определить одну четвертую часть площади по формуле
Таким образом, Вычисление длины дуги кривой Пусть кривая на плоскости имеет уравнение Разобьем отрезок
Обозначим
Определение 1. Если существует предел Теорема 1. Если на отрезке
Пример 1. Найти длину дуги кривой Решение. Область определения кривой
Если дуга задана параметрически уравнениями
Пример 2. Вычислить длину дуги кривой, заданной параметрически
Решение. Найдем
Вычисляем дифференциал длины дуги
Итак, длина дуги
Если кривая задана уравнениям в полярных координатах
где
Пример 3. Вычислить длину дуги кривой, заданной уравне-нием в полярных координатах
Решение. Найдем
Вычисляем дифференциал длины дуги:
тогда, длина дуги
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.247 (0.008 с.) |

 ;
;  ;
;
 .
.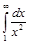 и установить его сходимость.
и установить его сходимость. .
.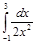 и установить его сходимость.
и установить его сходимость. подинтегральная функция неограниченна, т.е. она имеет разрыв внутри промежутка интегрирования.
подинтегральная функция неограниченна, т.е. она имеет разрыв внутри промежутка интегрирования.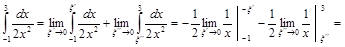

 .
. . (интеграл расходится)
. (интеграл расходится) функция
функция  , то согласно формуле
, то согласно формуле (1) (1)
(1) (1)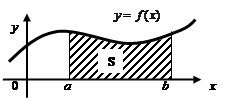
 на отрезке
на отрезке  , то криволинейная трапеция, ограниченная кривой
, то криволинейная трапеция, ограниченная кривой  , отрезком
, отрезком  и прямыми
и прямыми  и
и  , будет расположена ниже оси
, будет расположена ниже оси  . Определенный интеграл
. Определенный интеграл  , поэтому
, поэтому . (2)
. (2)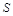 ограничена двумя функциями
ограничена двумя функциями 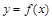 и
и  и прямыми
и прямыми  для
для  , то
, то . (3)
. (3)
 и
и  .
. , в которых
, в которых 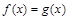 :
: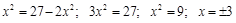 .
.
 , а площадь удвоить.
, а площадь удвоить.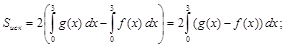
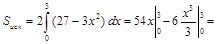
 кв. ед.
кв. ед. ,
,  ,
,  , причем
, причем  ,
,  , то площадь вычисляется по формуле
, то площадь вычисляется по формуле . (4)
. (4) Пример 2. Вычислить площадь фигуры, ограниченной эллипсом
Пример 2. Вычислить площадь фигуры, ограниченной эллипсом  ,
, 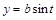 .
.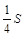 , где х изменяется от
, где х изменяется от  до 0. Найдем:
до 0. Найдем:
 .
. , откуда
, откуда 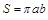 .
.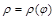 , то площадь криволинейной трапеции вычисляется по формуле
, то площадь криволинейной трапеции вычисляется по формуле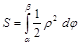 , (5)
, (5) и
и  – значение
– значение  в предельных точках.
в предельных точках.
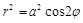 .
. .
. .
. этой кривой, ограниченной прямыми
этой кривой, ограниченной прямыми  и
и  .
. — соответствующие точки на графике
— соответствующие точки на графике 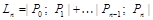 — длину ломаной с вершинами в этих точках.
— длину ломаной с вершинами в этих точках.
 , который не зависит от способа разбиения отрезка
, который не зависит от способа разбиения отрезка  . (1)
. (1) .
. . Тогда
. Тогда .
. , то ее длина находится по формуле
, то ее длина находится по формуле (2)
(2)
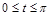 .
.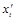 и
и 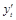 :
: ,
, 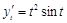 .
.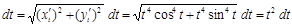 .
. ед. длины.
ед. длины. , где
, где  – полярный радиус, а
– полярный радиус, а 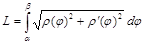 , (3)
, (3) .
.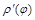 :
: .
. ,
, .
.


