
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование тригонометрических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Интегралы типа Интегралы типа В самом деле, если:
тогда
Пример 1. Вычислить интеграл Решение. Применяем универсальную подстановку
= Разложим дробь под интегралом на простые дроби:
Отсюда
Поэтому J = = = Пример 2. Вычислить интеграл Решение. Используем подстановку
= Если функция
или то можно использовать подстановку Пример 3. Вычислить интеграл Решение.
= = = Если функция четная относительно
то
Интегралы вида
Для интегрирования произведения синусов и косинусов разных аргументов применяются тригонометрические формулы:
Пример 4.
=
Интегрирование четных степеней синусов и косинусов
Здесь следует применять формулы понижения степени
Пример 5.
Пример 6.
= Пример 7.
Интегрирование нечетных степеней синусов и косинусов Интегрирование
где хотя бы один из показателей т и п – нечетный, (например,
где целесообразной будет подстановка Пример 8. Вычислить интеграл Решение.
Применяя подстановку
Пример 9. Вычислить интеграл Решение.
Применяя подстановки
имеем
Интегрирование целых степеней тангенса и котангенса Для интегрирования целых степеней тангенса и котангенса применяются формулы:
Пример 10. Вычислить интеграл Решение.
= = = Интегрирование иррациональных функций При интегрировании выражений, которые содержат дробные степени переменной интегрирования (т.е. иррациональности), методом подстановки сводят подинтегральную функцию к рациональной дроби. Рассмотрим несколько случаев. Интегрирование иррациональных выражений методом подстановки Подинтегральная функция является рациональной дробью относительно Пример 1. Найти интеграл Решение. Имеем: Общий знаменатель дробных показателей степеней
Интегрирование выражений, содержащих дробные степени линейного двучлена Подинтегральное выражение содержит дробные степени линейного двучлена Пример 2. Найти интеграл Решение. Пусть Поэтому
Интегрирование выражений вида
где В этом случае следует использовать тригонометрические подстановки соответственно После замены переменной имеем интеграл вида
который вычисляется с помощью подстановок или методом понижения степени с последующим возвращением к переменной х. Пример 3. Вычислить интеграл Решение. Сделаем подстановку Тогда
Применим понижение степени:
Возвращаемся к переменной х, подставляя
Интегрирование иррациональных выражений, содержащих квадратичный трехчлен 1) Интеграла вида Пример 4. Найти интеграл Решение.
2) Интеграла вида Пример 5. Найти интеграл Решение.
Упражнения к разделу 4.1 Вычислить неопределенный интеграл: 1). 2). 3). 4). 5). 6). 7). 8). Вычислить неопределенный интеграл методом подстановки: 9). 10). 11). 12). 13). 14). 15). Найти неопределенный интеграл методом интегрирования по частям: 9). 10). 11). 12). 13). 14). Найти неопределенный интеграл: 15). 16). 17). 18). 19). 20). Вычислить интегралы: 21). 22). 23). 24). 25). 26). 27). 28). 29). Вычислить интеграл: 30). 31). 32). 33). 34). 6. 35). 7. 36). 37). 38). 4.1.10 Задания для индивидуальной семестровой работы студентов к разделу 4.1 1 Найти неопределенный интеграл непосредственным интегрированием: 1
2
3
4
5
6
7
8 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2 Вычислить неопределенные интегралы 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Определенные и несобственные интегралы Определение и свойства определенного интеграла
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

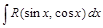
 и
и  , подстановкой
, подстановкой  можно привести к интегралам от рациональных функций.
можно привести к интегралам от рациональных функций. ;
;  ;
;  ;
;  ;
;  ,
,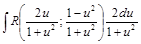 .
. .
.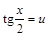 , тогда
, тогда  =
=  .
. .
.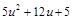 =
=  ;
;  ;
;  ;
;  .
. =
=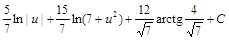 =
= .
.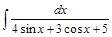 .
. =
= 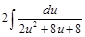 =
= =
=  =
=  .
.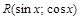 нечетная относительно
нечетная относительно  , т.е.
, т.е.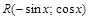 =
= 
 =
= 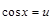 или
или  .
.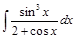 .
. =
= 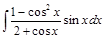 =
=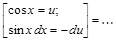 =
=  =
= 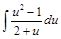 =
= =
=  =
= .
. .
. ;
; 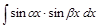 ;
;  .
.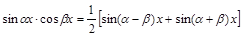
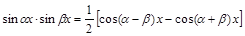

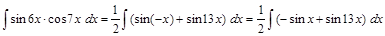 =
=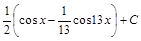 .
. .
. .
.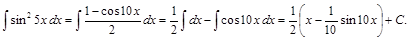
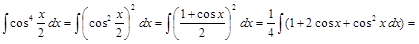 =
= 
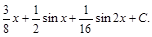


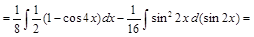
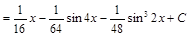 .
. ,
,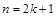 ) учитывая, что
) учитывая, что  , имеем:
, имеем: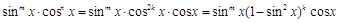 ,
, .
.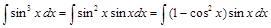 .
.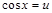 , имеем:
, имеем:
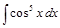 .
.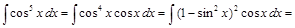
 .
. ,
,
 ;
;  .
. .
.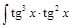 =
=  =
=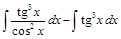 =
= 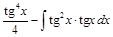 =
= =
=  =
= .
.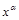 , где
, где  – дробное число. В этом случае вводят новую
– дробное число. В этом случае вводят новую , где
, где  – общий знаменатель дробных показателей степени переменной х.
– общий знаменатель дробных показателей степени переменной х. .
. .
. ,
,  ,
,  переменной х равняется 12. Поэтому сделаем подстановку
переменной х равняется 12. Поэтому сделаем подстановку 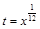 ,
,  ,
,  и получим:
и получим: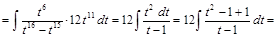

 .
. . В этом случае целесообразно сделать подстановку
. В этом случае целесообразно сделать подстановку  , где q – общий знаменатель дробных показателей степеней двучлена.
, где q – общий знаменатель дробных показателей степеней двучлена. .
. ,
,  ,
, 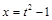 ,
,  .
. .
. ,
,  и
и  ,
, — рациональная функция
— рациональная функция .
. ,
, .
. .
. и
и  . После замены переменной имеем:
. После замены переменной имеем: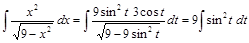 .
. .
. :
: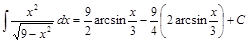 .
.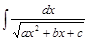 сводятся к табличным после выделения полного квадрата в знаменателе подинтегральной функции.
сводятся к табличным после выделения полного квадрата в знаменателе подинтегральной функции. .
. .
. после преобразований подинтегральной функции сводятся к выше рассмотренным. Для этого надо в числителе выделить дифференциал трехчлена, который стоит в знаменателе и разложить интеграл в сумму двух интегралов.
после преобразований подинтегральной функции сводятся к выше рассмотренным. Для этого надо в числителе выделить дифференциал трехчлена, который стоит в знаменателе и разложить интеграл в сумму двух интегралов.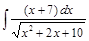 .
.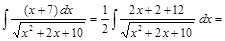 .
.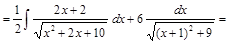
 .
.

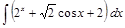
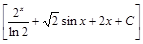




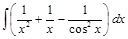



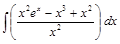

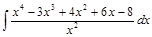




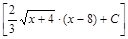

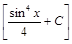

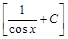





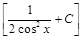




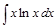
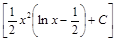
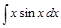

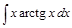

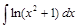














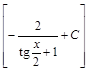

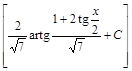





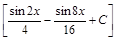






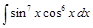

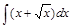



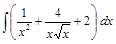
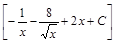
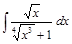

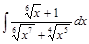
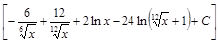



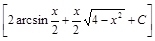
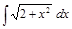
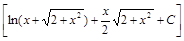
 ;
;  ;
;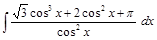 ;
;  ;
;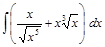 ;
;  .
. ;
; 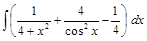 ;
;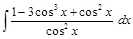 ;
;  ;
; ;
;  .
. ;
; 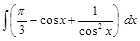 ;
; ;
;  ;
;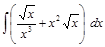 ;
;  .
. ;
; 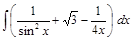 ;
; ;
;  ;
;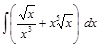 ;
; 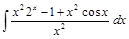 .
. ;
;  ;
; ;
;  ;
; ;
;  .
. ;
;  ;
; ;
;  ;
; ;
; 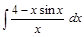 .
. ;
;  ;
; ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
;  ;
;  ;
;  .
. ;
;  ;
; ;
;  ;
; ;
;  .
.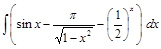 ;
;  ;
; ;
; 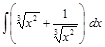 ;
;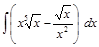 ;
;  .
. ;
;  ;
; ;
;  ;
; ;
;  .
. ;
;  ;
; ;
;  ;
; ;
;  .
.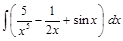 ;
; 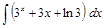 ;
; ;
; 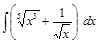 ;
;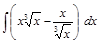 ;
;  .
. ;
;  ;
; ;
;  ;
;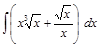 ;
;  .
.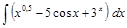 ;
;  ;
; ;
; 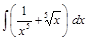 ;
; ;
;  .
.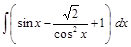 ;
;  ;
; ;
;  ;
; ;
; 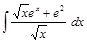 .
. ;
; 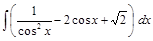 ;
; ;
;  ;
;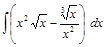 ;
; 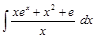 .
. ;
;  ;
; ;
;  ;
; ;
;  .
.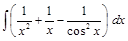 ;
;  ;
; ;
; 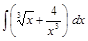 ;
;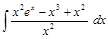 .
. ;
; 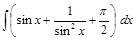 ;
; ;
; 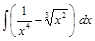 ;
; ;
;  .
.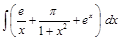 ;
;  ;
; ;
;  ;
; ;
;  .
. ;
;  ;
; ;
; 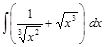 ;
; ;
;  .
.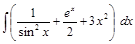 ;
;  ;
;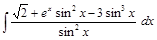 ;
;  ;
; ;
;  .
.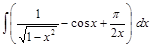 ;
; 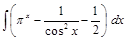 ;
; ;
; 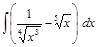 ;
; ;
; 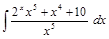 .
. ;
; 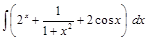 ;
;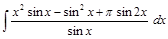 ;
; 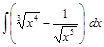 ;
;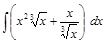 ;
;  .
. ;
;  ;
;  ;
; ;
;  .
.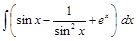 ;
;  ;
;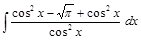 ;
; 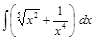 ;
; ;
; 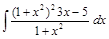 .
. ;
;  ;
; ;
;  ;
; ;
;  .
. ;
;  ;
;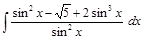 ;
;  ;
;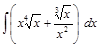 ;
;  .
. ;
; 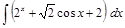 ;
; ;
;  ;
; ;
; 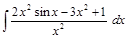 .
. ;
;  ;
; 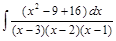 .
. ;
; 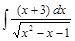 ;
;  .
. ;
;  ;
; 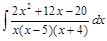 .
. ;
; 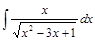 ;
;  .
. ;
;  ;
;  .
.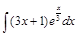 ;
; 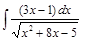 ;
;  .
. ;
;  ;
; 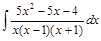 .
. ;
; 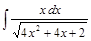 ;
;  .
. ;
;  ;
;  .
. ;
; 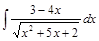 ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
. ;
;  ;
; 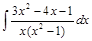 .
.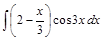 ;
; 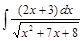 ;
; 
 ;
;  ;
;  .
.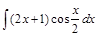 ;
;  ;
;  .
.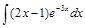 ;
;  ;
; 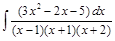 .
.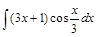 ;
; 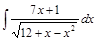 ;
; 
 ;
; 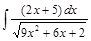 ;
;  .
.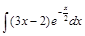 ;
;  ;
; 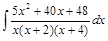 .
. ;
;  ;
;  .
. ;
; 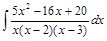 .
.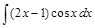 ;
;  .
. ;
;  ;
;  .
. ;
; 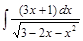 ;
;  .
. ;
;  ;
;  .
. ;
; 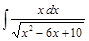 ;
; 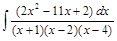 .
.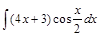 ;
;  .
. ;
;  ;
;  .
. ;
;  ;
;  .
.


