
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование заменой переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся. Если в неопределенном интеграле
Эта формула называется формулой замены переменной в неопределенном интеграле.
15 Метод интегрирования по частям. Рассмотрим функции
Проинтегрировав левую и правую части последнего равенства, получим:
Полученное равенство перепишем в виде:
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл Замечание В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
18 интегрирование неправильных рациональных дробей
19 разложение правильной дроби
Интегрирование правильных рациональных дробей Рациональная дробь Пример Рациональная дробь Выражения Если дробь неправильная, то, разделив числитель на знаменатель по правилу деления многочленов, можно получить многочлен плюс правильную дробь. Примеры интегрирования правильных рациональных дробей Пример Задание. Представить неправильную дробь Решение. Поделим числитель на знаменатель дроби в столбик (деление проводится до тех пор, пока степень остатка не будет меньше степени делителя):
Таким образом,
Ответ. Пример Задание. Найти интеграл Решение. Так как подынтегральная функция
То есть,
Тогда интеграл
Ответ. 20 понятие определенного интеграла Определённым интегралом от непрерывной функции f (x) на конечном отрезке [ a, b ] (где
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [ a, b ] – отрезком интегрирования. Таким образом, если F (x) – какая-нибудь первообразная функция для f (x), то, согласно определению,
При a = b по определению принимается
Равенство (38) называется формулой Ньютона-Лейбница. Разность F (b) – F (a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
21 Геометрический смысл определенного интеграла. Определённый интеграл
Свойства определенного интеграла 1.Определенный интеграл от единицы равен длине интервала интегрирования:
2.Постоянный множитель можно выносить за знак определенного интеграла:
3.Определенный интеграл от суммы функций равен сумме интегралов от этих функций:
4.Определенный интеграл от разности функций равен разности интегралов от этих функций:
5.Если верхний предел равен нижнему, то определенный интеграл равен нулю:
6.При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:
7.Пусть точка c принадлежит отрезку [ a, b ]. Тогда определенный интеграл от функции f (x) на отрезке[ a, b ] равен сумме интегралов на частичных промежутках [ a, c ] и [ c, b ]:
8.Определенный интеграл от неотрицательной функции всегда больше или равен нулю:
9.Определенный интеграл от неположительной функции всегда меньше или равен нулю:
10. Формула Ньютона-Лейбница
11. Метод подстановки для определенного интеграла
12. Интегрирование по частям
22 Оценка определенного интеграла. Если m и M ¾ соответственно наименьшее и наибольшее значения непрерывной функции f(x) на отрезке [ a, b ], то
Теорема о среднем Если функция f(x) непрерывна на отрезке [ a, b ], то на этом отрезке существует точка С такая, что
Величина 23 Интеграл с переменным верхним пределом. Пусть на отрезке [ a, b ] задана непрерывная функция f (x), тогда для любого x
задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
24 Формула Ньютона- Лейбница Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Если F (x) - первообразная функции f (x) на[ a, b ], то
25 Замена переменной и интегрирование по частям в определенном интеграле. Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы для определённого:
Предполагается, что нахождение интеграла В противном случае применение метода неоправданно. Для определённого интеграла В целом аналогично случаю неопределённого интеграла:
Данные формулы справедливы, если каждая из функций
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.203 (0.006 с.) |

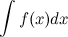 сделать подстановку
сделать подстановку  , где функция
, где функция  - функция с непрерывной первой производной, то тогда
- функция с непрерывной первой производной, то тогда  и согласно свойству 6 неопределенного интеграла имеем, что:
и согласно свойству 6 неопределенного интеграла имеем, что:
 и
и  , которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:
, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:


 можно свести к нахождению интеграла
можно свести к нахождению интеграла 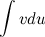 , который может быть более простым.
, который может быть более простым.
 называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е.
называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. 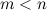 . Если же
. Если же 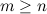 , то дробь называется неправильной.
, то дробь называется неправильной. является правильной.
является правильной. и
и  - неправильные рациональные дроби.
- неправильные рациональные дроби.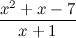 в виде суммы многочлена и правильной дроби.
в виде суммы многочлена и правильной дроби.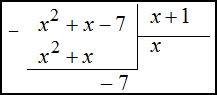
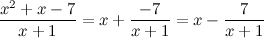


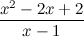 является неправильной рациональной дробью (так как степень числителя больше степени знаменателя), то выделим целую часть, для этого числитель поделим на знаменатель в столбик:
является неправильной рациональной дробью (так как степень числителя больше степени знаменателя), то выделим целую часть, для этого числитель поделим на знаменатель в столбик: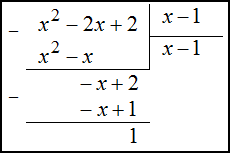


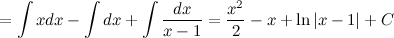
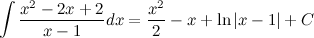
 ) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись
) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись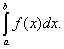
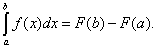 (38)
(38)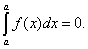

 (39)
(39) численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми  и
и 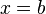 и графиком функции
и графиком функции 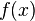 .
.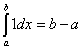


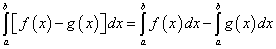
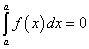




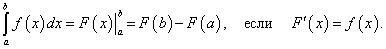
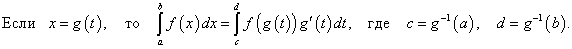


 . (6)
. (6) называется средним значением функции f(x) на отрезке [a, b].
называется средним значением функции f(x) на отрезке [a, b]. [ a, b ] существует функция:
[ a, b ] существует функция: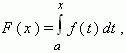

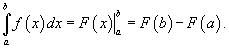

 проще, чем
проще, чем  .
.

 и
и  непрерывно дифференцируемы на области интегрирования.
непрерывно дифференцируемы на области интегрирования.


