Замена переменной в неопределенном интеграле
Похожие статьи вашей тематики
Это один из двух самых мощных методов вычисления интегралов. Суть его примерно состоит в следующем. Допустим необходимо вычислить неопределенный интеграл от функции  , переменная интегрирования в котором обозначена буквой , переменная интегрирования в котором обозначена буквой 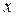 , и этот интеграл кажется сложным для вычисления (не проходят ни метод непосредственного интегрирования, ни внесение под знак дифференциала и т.д.). Тогда есть смысл перейти к другой (новой) переменной интегрирования (скажем , и этот интеграл кажется сложным для вычисления (не проходят ни метод непосредственного интегрирования, ни внесение под знак дифференциала и т.д.). Тогда есть смысл перейти к другой (новой) переменной интегрирования (скажем 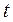 ), указав, конечно, связь между старой переменной ), указав, конечно, связь между старой переменной 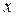 и новой переменной и новой переменной 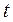 . Эта связь может выражать либо . Эта связь может выражать либо 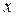 как функцию от как функцию от 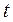 (вида (вида 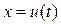 ), либо ), либо 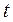 как функцию от как функцию от 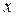 (вида (вида 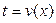 ). Тогда имеется правило (оно и называется заменой переменных), позволяющее исходный интеграл записать в новой переменной ). Тогда имеется правило (оно и называется заменой переменных), позволяющее исходный интеграл записать в новой переменной 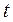 (новая переменная интегрирования). Этот новый интеграл по переменной (новая переменная интегрирования). Этот новый интеграл по переменной 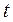 может (при удачном выборе связи между новой и старой переменной) оказаться более простым для вычисления. Если мы его вычислим, то получим ответ, естественно, в новой же переменной может (при удачном выборе связи между новой и старой переменной) оказаться более простым для вычисления. Если мы его вычислим, то получим ответ, естественно, в новой же переменной 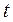 . Если после этого в полученном ответе перейти опять к старой переменной . Если после этого в полученном ответе перейти опять к старой переменной 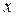 (используя назначенную выше связь между старой и новой переменной), то получим ответ для исходного интеграла. Формально этот прием обосновывается следующей теоремой. (используя назначенную выше связь между старой и новой переменной), то получим ответ для исходного интеграла. Формально этот прием обосновывается следующей теоремой.
Теорема (замена переменной в неопределенном интеграле).
Пусть
1) Функция  имеет первообразную (а значит и интеграл) на интервале имеет первообразную (а значит и интеграл) на интервале  (как указывалось выше, таковы, например, все непрерывные функции). (как указывалось выше, таковы, например, все непрерывные функции).
2) Функция 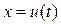 дифференцируема на некотором интервале дифференцируема на некотором интервале 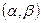 и переводит этот интервал в интервал и переводит этот интервал в интервал  . .
Тогда функция  тоже имеет первообразную (и интеграл) на тоже имеет первообразную (и интеграл) на 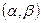 и справедлива формулы замены переменной: и справедлива формулы замены переменной:
(1) 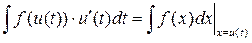 , ,
(2) 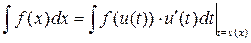  
Вертикальная черта справа означает, что в полученном ответе необходимо перейти к соответствующей переменной по соответствующей формуле связи старой и новой переменной. В каждой из написанных формул в левом интеграле произведена замена переменной 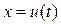 , но в первом интеграле , но в первом интеграле  – старая переменная, а – старая переменная, а  – новая, а во втором наоборот. Доказывается эта теорема несложно с помощью правила (*) и формулы для производной от сложной функции. – новая, а во втором наоборот. Доказывается эта теорема несложно с помощью правила (*) и формулы для производной от сложной функции.
При решении примеров на формулу (1) или (2) удобнее всего пользоваться следующими формальными рассуждениями. Допустим, нам нужно вычислить 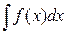 , но в исходной переменной , но в исходной переменной  этот интеграл кажется сложным для вычисления. Переходим к новой переменной интегрирования этот интеграл кажется сложным для вычисления. Переходим к новой переменной интегрирования  , указав соответствующую формульную связь старой и новой переменной: , указав соответствующую формульную связь старой и новой переменной: 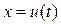 . Теперь можно формально подставить в . Теперь можно формально подставить в 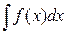 везде вместо везде вместо  его выражение его выражение 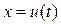 через через  , понимая при этом , понимая при этом 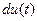 как дифференциал функции: как дифференциал функции: 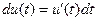 . Тогда исходный . Тогда исходный 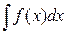 переходит в переходит в 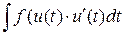 , что как раз представляет собой правую часть формулы (2). После вычисления полученного интеграла остается перейти обратно в ответе к исходной переменной , что как раз представляет собой правую часть формулы (2). После вычисления полученного интеграла остается перейти обратно в ответе к исходной переменной  . Оформлять такое решение будем следующим образом: . Оформлять такое решение будем следующим образом:
(3) 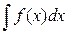 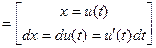  . .
Единственным (но самым нетривиальным) творческим моментом при применении формул замены переменной (1) или (2) является выбор формы связи 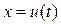 или или 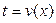 старой и новой переменных. Как же выбирать связь этих переменных? Критерий один. Поскольку при замене переменной мы переходим от вычисления одного (исходного) интеграла к другому, то связь переменных надо выбирать такой, чтобы новый интеграл оказался бы для вычисления проще, чем исходный (иначе никакого смысла в замене одного интеграла другим не будет). Однако выбор такой связи не всегда очевиден и во многих случаях является искусством. Но для некоторых типов интегралов (в следующих параграфах мы коснемся части из них) форма упрощающей замены переменной известна. старой и новой переменных. Как же выбирать связь этих переменных? Критерий один. Поскольку при замене переменной мы переходим от вычисления одного (исходного) интеграла к другому, то связь переменных надо выбирать такой, чтобы новый интеграл оказался бы для вычисления проще, чем исходный (иначе никакого смысла в замене одного интеграла другим не будет). Однако выбор такой связи не всегда очевиден и во многих случаях является искусством. Но для некоторых типов интегралов (в следующих параграфах мы коснемся части из них) форма упрощающей замены переменной известна.
Пример 1. Вычислить интеграл 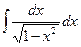 . .
Решение. Вообще-то такой интеграл есть в простой таблице интегралов под
№ 13 при 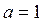 , но теперь можно узнать, почему ответ имеет именно такой вид. Основная кажущаяся сложность вычисления интеграла – наличие корня в знаменателе. Какой же формулой , но теперь можно узнать, почему ответ имеет именно такой вид. Основная кажущаяся сложность вычисления интеграла – наличие корня в знаменателе. Какой же формулой 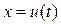 заменить в интеграле заменить в интеграле  через через  , чтобы квадратный корень после этого исчез? Квадратный корень исчезнет, если под корнем появится некоторое выражение в квадрате. Вспомним, что по основному тригонометрическому тождеству , чтобы квадратный корень после этого исчез? Квадратный корень исчезнет, если под корнем появится некоторое выражение в квадрате. Вспомним, что по основному тригонометрическому тождеству 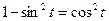 . Поэтому если сделать замену . Поэтому если сделать замену 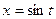 , то при подстановке такого , то при подстановке такого  под интеграл корень должен исчезнуть и, по-видимому, интеграл окажется проще. Именно поэтому выбираем замену переменной под интеграл корень должен исчезнуть и, по-видимому, интеграл окажется проще. Именно поэтому выбираем замену переменной 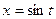 (т.е. выбираем (т.е. выбираем 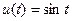 ). Далее действуем по схеме (3): ). Далее действуем по схеме (3):
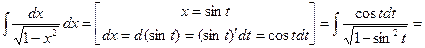 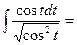 
 . .
Как видно, по новой переменной  функция под интегралом значительно упростилась, став равной 1. По самой первой формуле из простой таблицы интегралов (с учетом того, что переменная интегрирования теперь обозначена не буквой функция под интегралом значительно упростилась, став равной 1. По самой первой формуле из простой таблицы интегралов (с учетом того, что переменная интегрирования теперь обозначена не буквой  , а буквой , а буквой  ) получаем ответ в новой переменной ) получаем ответ в новой переменной  : : 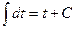 . Осталось в этом ответе обратно выразить новую переменную . Осталось в этом ответе обратно выразить новую переменную  через исходную переменную через исходную переменную  . Если . Если 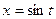 , то в обратную сторону , то в обратную сторону  выражается через выражается через  с помощью обратной функции: с помощью обратной функции:  . Поэтому ответ в исходной переменной . Поэтому ответ в исходной переменной 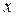 будет будет  . Итак, . Итак,
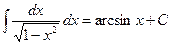 , ,
что соответствует табличной формуле при 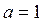 . .
Пример 2. Вычислить интеграл 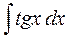 . .
Решение.  . Далее для таких типов интегралов (когда выражение под интегралом содержит . Далее для таких типов интегралов (когда выражение под интегралом содержит 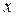 только под знаком косинуса, но перед только под знаком косинуса, но перед  есть множитель есть множитель  ) будет дана рекомендация введения новой переменной ) будет дана рекомендация введения новой переменной 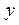 по формуле по формуле 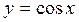 . Сделаем такую замену переменной в предлагаемом интеграле . Сделаем такую замену переменной в предлагаемом интеграле 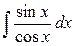 . Тогда в знаменателе . Тогда в знаменателе  можно будет сразу заменить на можно будет сразу заменить на  . Но остается под интегралом . Но остается под интегралом 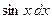 , а при замене переменной в интеграле должна остаться только новая переменная , а при замене переменной в интеграле должна остаться только новая переменная  , а в конце должно стоять , а в конце должно стоять 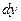 . Посмотрим, во что должно перейти выражение . Посмотрим, во что должно перейти выражение 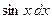 при переходе к новой переменной при переходе к новой переменной  . Для этого вычислим дифференциал функции . Для этого вычислим дифференциал функции 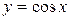 : : 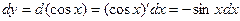 , т.е. , т.е. 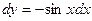 . Отсюда сразу получается, что выражение . Отсюда сразу получается, что выражение 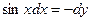 . Таким образом, оформляем следующую формальную запись: . Таким образом, оформляем следующую формальную запись:
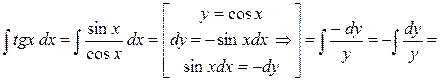 {формула 4 из простой таблицы интегралов} {формула 4 из простой таблицы интегралов}  ={возвращаясь к старой переменной ={возвращаясь к старой переменной 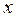 по формуле по формуле 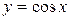 } = } =  . Итак, . Итак,
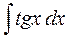 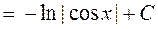 . .
Интегрирование по частям
Это второй из наиболее общих специальных методов вычисления интегралов. Пусть функции  и и 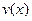 дифференцируемы (т.е. имеют производную) на рассматриваемом интервале изменения дифференцируемы (т.е. имеют производную) на рассматриваемом интервале изменения  . Тогда верно равенство . Тогда верно равенство
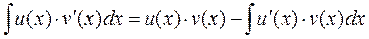
Данная формула и называется формулой интегрирования по частям, а доказывается она легко применением правила (*) и формулы производной произведения. Эту формулу можно записать и в более компактной форме, если заметить, что по определению дифференциала функции 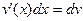 , а , а 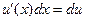 . Делая соответствующую подстановку в написанной формуле и опуская для краткости обозначение аргумента х у функций, получим . Делая соответствующую подстановку в написанной формуле и опуская для краткости обозначение аргумента х у функций, получим

Именно в такой форме формула записана во многих учебниках. Но, думается, удобнее ее применять в первоначальной форме, тоже опустив для краткости обозначение аргумента х у функций:
(1) 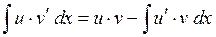 . .
Доказательство формулы (1) достаточно простое. По правилу (*) (в параграфе «Основные понятия») для того, чтобы убедиться, что правая часть формулы (1) действительно представляет собой значение интеграла в левой части, надо взять производную от правой части (1) и получить при этом подынтегральную функцию  в интеграле слева. Проделаем это: в интеграле слева. Проделаем это: 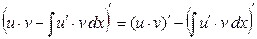 ={используем формулу производной произведения и свойство 1 неопределенного интеграла в параграфе «Свойства неопределенного интеграла» о том, что производная от интеграла равна подынтегральной функции} ={используем формулу производной произведения и свойство 1 неопределенного интеграла в параграфе «Свойства неопределенного интеграла» о том, что производная от интеграла равна подынтегральной функции} 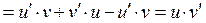 , что и требовалось. , что и требовалось.
Формула интегрирования по частям (как и замены переменной) сводит вычисление одного интеграла (в левой части) к вычислению другого интеграла (в правой части). Поэтому ее целесообразно применять только тогда, когда второй интеграл оказывается более простым для вычисления, чем первый. Формула интегрирования по частям применяется для интегрирования произведения функций разного типа (например, тригонометрической и степенной, тригонометрической и показательной, степенной и показательной (логарифмической) и т.д.). Далее будут даны более конкретные рекомендации. Для применения формулы (1) интегрирования по частям надо разбить подынтегральную функцию на 2 сомножителя, взяв один из них за u, а другой за v′ (причем очень важно правильно выбрать, что за что брать – от этого зависит успех применения формулы). Потом по этим данным нужно найти u′ и v для подстановки их в правую часть формулы (1). Выражение для u′ получается из u обычным дифференцированием, а выражение для v из v′ (как и всякое восстановление функции по известной ее производной) получается интегрированием: 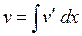 (см. свойство 2 интеграла), причем при вычислении этого интеграла достаточно найти только одну первообразную, поэтому «+С» потом можно не писать. (см. свойство 2 интеграла), причем при вычислении этого интеграла достаточно найти только одну первообразную, поэтому «+С» потом можно не писать.
Пример 1. Вычислить 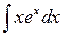 интегрированием по частям (впрочем, по-другому и не получится). интегрированием по частям (впрочем, по-другому и не получится).
Решение. Применяем формулу (1), взяв 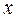 за за 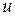 , а , а  за за 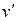 : :
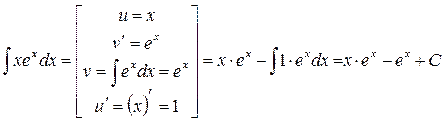
Между большими квадратными скобками записывается комментарий, описывающий подготовку к применению формулы (1) интегрирования по частям. Содержимое комментария, в принципе, не является частью формулы и записывается для удобства.
Дадим теперь обещанные конкретные рекомендации по применению этой формулы. Чаще всего формула интегрирования по частям (1) применяется для вычисления интегралов следующих типов (одновременно даны рекомендации − что брать за 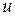 , а что за , а что за 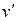 ): ):
1.  2. 2. 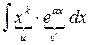 3. 3. 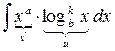 4. 4.  . .
В написанных интегралах 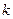 − неотрицательное целое число, a и b – произвольные числа (в основании логарифма, естественно, b>0 и b ≠ 1). Причем там, где стоит − неотрицательное целое число, a и b – произвольные числа (в основании логарифма, естественно, b>0 и b ≠ 1). Причем там, где стоит 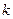 в показателе степени, интегрирование по частям приходится проводить в показателе степени, интегрирование по частям приходится проводить 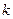 раз, пока не получится интеграл из таблицы интегралов. раз, пока не получится интеграл из таблицы интегралов.
Пример 2. Вычислить  . .
Решение. Это интеграл первого из перечисленных выше типов при  и и 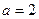 , поэтому перед применением формулы (1) делаем рекомендуемый выбор функций , поэтому перед применением формулы (1) делаем рекомендуемый выбор функций 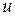 и и 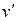 : :
 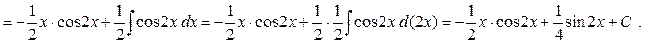
Пример 3. Вычислить 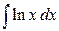 . .
Решение. В данном примере под интегралом только одна функция, поэтому казалось бы формулу интегрирования по частям применять нельзя. Однако всегда вторым множителем можно сделать единицу:  . Теперь видно, что это интеграл третьего типа при . Теперь видно, что это интеграл третьего типа при 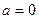 (так как (так как  ), ), 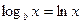 и и  . Применяем формулу (1): . Применяем формулу (1):
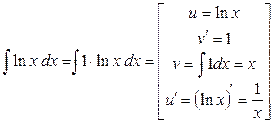 = = 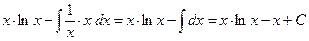 . .
Пример 4. Вычислить 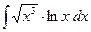 . .
Решение. Поскольку  , то это снова интеграл третьего типа при , то это снова интеграл третьего типа при 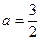 , , 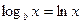 и и  : :
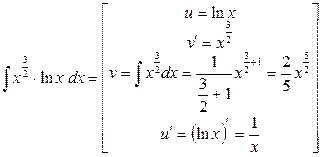  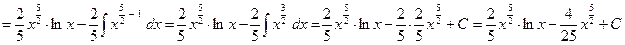 . .
Пример 5. Вычислить 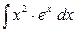 . .
Решение. Это интеграл второго типа при 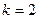 (а потому формулу интегрирования по частям придется применять 2 раза) и (а потому формулу интегрирования по частям придется применять 2 раза) и  : :
(2)  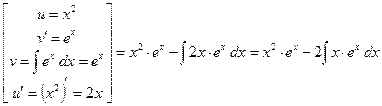 . .
Справа в (2) опять получился интеграл того же типа, но при  . Вычислим его снова по формуле интегрирования по частям и подставим в (2): . Вычислим его снова по формуле интегрирования по частям и подставим в (2): 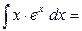 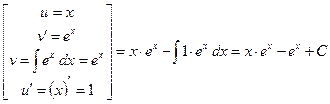 . Подставляя в (2), окончательно получим: . Подставляя в (2), окончательно получим:  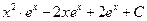 . .
Пример 6. Вычислить 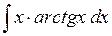 . .
Решение. Это интеграл четвертого типа из тех, которые выше рекомендовано вычислять методом интегрирования по частям (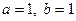 ): ): 
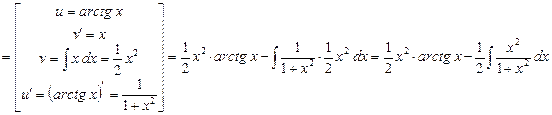 . Вычислим последний интеграл, приведя его к табличным: . Вычислим последний интеграл, приведя его к табличным: 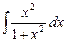 = = 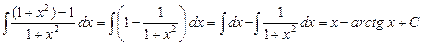 . Подставляя полученное значение интеграла в предыдущее выражение, окончательно получим: . Подставляя полученное значение интеграла в предыдущее выражение, окончательно получим:   . .
Рассмотрим теперь некоторые специальные приемы для интегрирования некоторых классов функций.
Интегрирование выражений, содержащих логарифмы
Если логарифм (или его натуральная степень) под интегралом умножается на некоторую степень  , то интеграл вычисляется методом интегрирования по частям, что разобрано выше. Рассмотрим теперь интегрирование выражений, в которых аргумент , то интеграл вычисляется методом интегрирования по частям, что разобрано выше. Рассмотрим теперь интегрирование выражений, в которых аргумент  в числителе входит только под знаком логарифма (для простоты – натурального). Это интегралы вида в числителе входит только под знаком логарифма (для простоты – натурального). Это интегралы вида 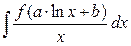 . Здесь под . Здесь под 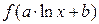 понимается любая формула, в которую аргумент понимается любая формула, в которую аргумент  входит только в комбинации входит только в комбинации 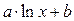 (где (где  и и 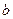 − некоторые числа), причем вся эта формула обязательно под интегралом должна делиться на − некоторые числа), причем вся эта формула обязательно под интегралом должна делиться на  (это деление может быть и представлено и умножением на (это деление может быть и представлено и умножением на 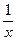 ). В этом случае рекомендуется замена переменной в интеграле по формуле ). В этом случае рекомендуется замена переменной в интеграле по формуле 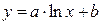 (так новая переменная (так новая переменная  связана с исходной переменной связана с исходной переменной  ). Найдем дифференциал ). Найдем дифференциал 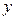 : : 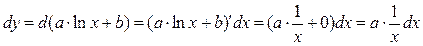 . Таким образом, . Таким образом,  , откуда , откуда 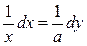 . Поэтому при замене переменной в интеграле вида . Поэтому при замене переменной в интеграле вида 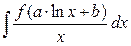 (который может быть записан и в виде (который может быть записан и в виде  ) при указанной замене ) при указанной замене 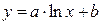 выражение выражение 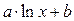 везде заменяется на везде заменяется на 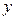 , а , а 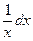 заменяется на заменяется на 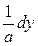 . Оформляется это следующей записью: . Оформляется это следующей записью:
(1) 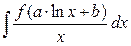 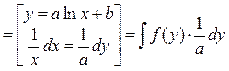 . .
Отметим, что в часто встречающемся частном случае интеграла вида 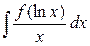 (т.е. при (т.е. при  ) формула (1) переходит в более простую: ) формула (1) переходит в более простую:
(2) 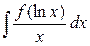 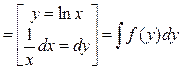 . .
Приведем примеры на описанный прием вычисления интегралов.
Пример 1. Вычислить  . .
Решение. В числителе  входит только в комбинации входит только в комбинации 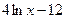 и есть и есть  в знаменателе, поэтому используем замену переменной (1) (при в знаменателе, поэтому используем замену переменной (1) (при 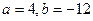 ): ): 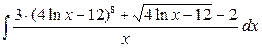 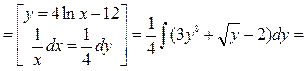 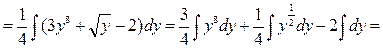 { остались интегралы из простой таблицы, только переменная интегрирования теперь обозначена не { остались интегралы из простой таблицы, только переменная интегрирования теперь обозначена не  , а , а  , поэтому и ответ будет с этой переменной} , поэтому и ответ будет с этой переменной} 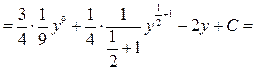 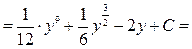 { возвращаемся в полученном ответе к старой переменной { возвращаемся в полученном ответе к старой переменной  , учитывая, что , учитывая, что 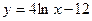 }= }= 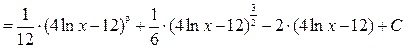 . Окончательно: . Окончательно:
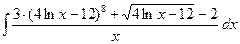 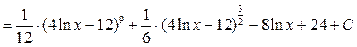 . .
Замечание. В конце ответа можно было бы заменить 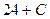 одной буквой одной буквой 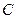 − от этого все множество соответствующих первообразных не изменилось бы. − от этого все множество соответствующих первообразных не изменилось бы.
Пример 2. Вычислить 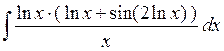 . .
Решение. В числителе  входит только под знаком логарифма есть входит только под знаком логарифма есть  в знаменателе, поэтому используем замену переменной (2): в знаменателе, поэтому используем замену переменной (2): 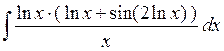 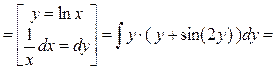 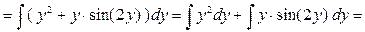 { первый интеграл – табличный, а для вычисления второго воспользуемся результатом примера 2 предыдущего параграфа { первый интеграл – табличный, а для вычисления второго воспользуемся результатом примера 2 предыдущего параграфа  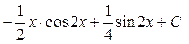 , заменив, естественно, , заменив, естественно,  на на  }= }= 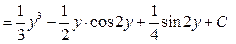 ={ возвращаемся в полученном ответе к старой переменной ={ возвращаемся в полученном ответе к старой переменной  , учитывая, что , учитывая, что  } } 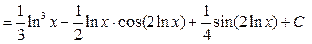 . Итак, . Итак, 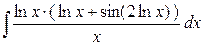 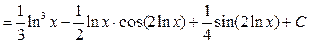 . .
|



 , переменная интегрирования в котором обозначена буквой
, переменная интегрирования в котором обозначена буквой 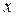 , и этот интеграл кажется сложным для вычисления (не проходят ни метод непосредственного интегрирования, ни внесение под знак дифференциала и т.д.). Тогда есть смысл перейти к другой (новой) переменной интегрирования (скажем
, и этот интеграл кажется сложным для вычисления (не проходят ни метод непосредственного интегрирования, ни внесение под знак дифференциала и т.д.). Тогда есть смысл перейти к другой (новой) переменной интегрирования (скажем 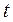 ), указав, конечно, связь между старой переменной
), указав, конечно, связь между старой переменной 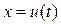 ), либо
), либо 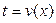 ). Тогда имеется правило (оно и называется заменой переменных), позволяющее исходный интеграл записать в новой переменной
). Тогда имеется правило (оно и называется заменой переменных), позволяющее исходный интеграл записать в новой переменной  (как указывалось выше, таковы, например, все непрерывные функции).
(как указывалось выше, таковы, например, все непрерывные функции).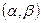 и переводит этот интервал в интервал
и переводит этот интервал в интервал  тоже имеет первообразную (и интеграл) на
тоже имеет первообразную (и интеграл) на 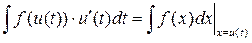 ,
,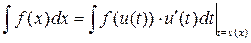

 – старая переменная, а
– старая переменная, а  – новая, а во втором наоборот. Доказывается эта теорема несложно с помощью правила (*) и формулы для производной от сложной функции.
– новая, а во втором наоборот. Доказывается эта теорема несложно с помощью правила (*) и формулы для производной от сложной функции.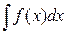 , но в исходной переменной
, но в исходной переменной  этот интеграл кажется сложным для вычисления. Переходим к новой переменной интегрирования
этот интеграл кажется сложным для вычисления. Переходим к новой переменной интегрирования  как дифференциал функции:
как дифференциал функции: 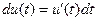 . Тогда исходный
. Тогда исходный 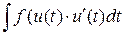 , что как раз представляет собой правую часть формулы (2). После вычисления полученного интеграла остается перейти обратно в ответе к исходной переменной
, что как раз представляет собой правую часть формулы (2). После вычисления полученного интеграла остается перейти обратно в ответе к исходной переменной 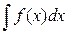
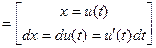
 .
.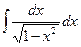 .
.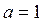 , но теперь можно узнать, почему ответ имеет именно такой вид. Основная кажущаяся сложность вычисления интеграла – наличие корня в знаменателе. Какой же формулой
, но теперь можно узнать, почему ответ имеет именно такой вид. Основная кажущаяся сложность вычисления интеграла – наличие корня в знаменателе. Какой же формулой 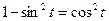 . Поэтому если сделать замену
. Поэтому если сделать замену 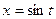 , то при подстановке такого
, то при подстановке такого 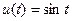 ). Далее действуем по схеме (3):
). Далее действуем по схеме (3):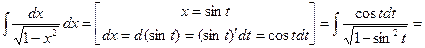
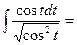

 .
.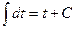 . Осталось в этом ответе обратно выразить новую переменную
. Осталось в этом ответе обратно выразить новую переменную  . Поэтому ответ в исходной переменной
. Поэтому ответ в исходной переменной  . Итак,
. Итак,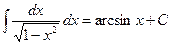 ,
,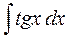 .
. . Далее для таких типов интегралов (когда выражение под интегралом содержит
. Далее для таких типов интегралов (когда выражение под интегралом содержит  есть множитель
есть множитель  ) будет дана рекомендация введения новой переменной
) будет дана рекомендация введения новой переменной 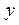 по формуле
по формуле 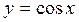 . Сделаем такую замену переменной в предлагаемом интеграле
. Сделаем такую замену переменной в предлагаемом интеграле 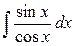 . Тогда в знаменателе
. Тогда в знаменателе  можно будет сразу заменить на
можно будет сразу заменить на  . Но остается под интегралом
. Но остается под интегралом 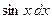 , а при замене переменной в интеграле должна остаться только новая переменная
, а при замене переменной в интеграле должна остаться только новая переменная 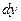 . Посмотрим, во что должно перейти выражение
. Посмотрим, во что должно перейти выражение 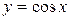 :
: 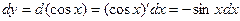 , т.е.
, т.е. 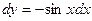 . Отсюда сразу получается, что выражение
. Отсюда сразу получается, что выражение 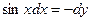 . Таким образом, оформляем следующую формальную запись:
. Таким образом, оформляем следующую формальную запись: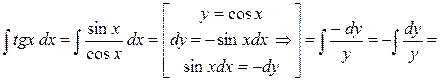 {формула 4 из простой таблицы интегралов}
{формула 4 из простой таблицы интегралов}  ={возвращаясь к старой переменной
={возвращаясь к старой переменной 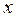 по формуле
по формуле  . Итак,
. Итак,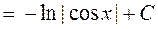 .
.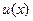 и
и 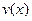 дифференцируемы (т.е. имеют производную) на рассматриваемом интервале изменения
дифференцируемы (т.е. имеют производную) на рассматриваемом интервале изменения 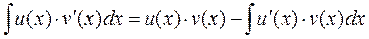
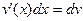 , а
, а 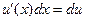 . Делая соответствующую подстановку в написанной формуле и опуская для краткости обозначение аргумента х у функций, получим
. Делая соответствующую подстановку в написанной формуле и опуская для краткости обозначение аргумента х у функций, получим
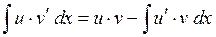 .
. в интеграле слева. Проделаем это:
в интеграле слева. Проделаем это: 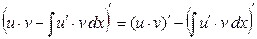 ={используем формулу производной произведения и свойство 1 неопределенного интеграла в параграфе «Свойства неопределенного интеграла» о том, что производная от интеграла равна подынтегральной функции}
={используем формулу производной произведения и свойство 1 неопределенного интеграла в параграфе «Свойства неопределенного интеграла» о том, что производная от интеграла равна подынтегральной функции} 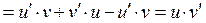 , что и требовалось.
, что и требовалось.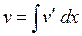 (см. свойство 2 интеграла), причем при вычислении этого интеграла достаточно найти только одну первообразную, поэтому «+С» потом можно не писать.
(см. свойство 2 интеграла), причем при вычислении этого интеграла достаточно найти только одну первообразную, поэтому «+С» потом можно не писать.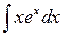 интегрированием по частям (впрочем, по-другому и не получится).
интегрированием по частям (впрочем, по-другому и не получится).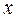 за
за 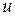 , а
, а  за
за 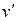 :
: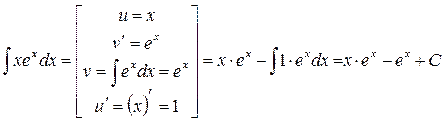
 2.
2. 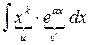 3.
3. 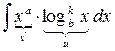 4.
4.  .
.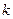 − неотрицательное целое число, a и b – произвольные числа (в основании логарифма, естественно, b>0 и b ≠ 1). Причем там, где стоит
− неотрицательное целое число, a и b – произвольные числа (в основании логарифма, естественно, b>0 и b ≠ 1). Причем там, где стоит  .
. и
и 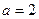 , поэтому перед применением формулы (1) делаем рекомендуемый выбор функций
, поэтому перед применением формулы (1) делаем рекомендуемый выбор функций 
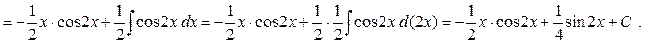
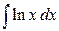 .
. . Теперь видно, что это интеграл третьего типа при
. Теперь видно, что это интеграл третьего типа при 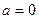 (так как
(так как  ),
), 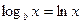 и
и 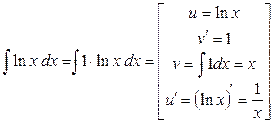 =
= 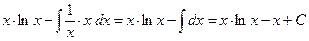 .
. .
. , то это снова интеграл третьего типа при
, то это снова интеграл третьего типа при  ,
, 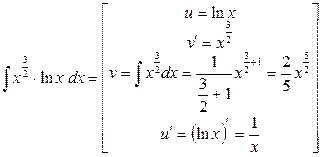

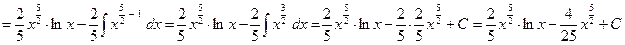 .
.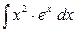 .
.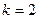 (а потому формулу интегрирования по частям придется применять 2 раза) и
(а потому формулу интегрирования по частям придется применять 2 раза) и  :
:
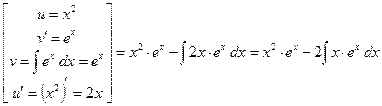 .
.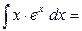
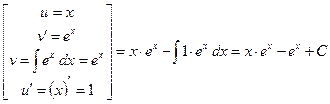 . Подставляя в (2), окончательно получим:
. Подставляя в (2), окончательно получим: 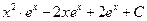 .
.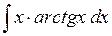 .
.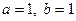 ):
): 
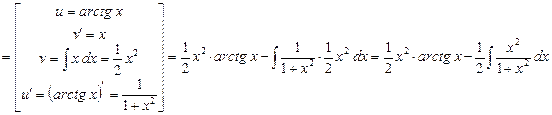 . Вычислим последний интеграл, приведя его к табличным:
. Вычислим последний интеграл, приведя его к табличным: 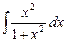 =
= 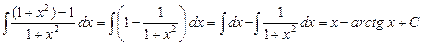 . Подставляя полученное значение интеграла в предыдущее выражение, окончательно получим:
. Подставляя полученное значение интеграла в предыдущее выражение, окончательно получим:  .
.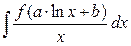 . Здесь под
. Здесь под 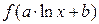 понимается любая формула, в которую аргумент
понимается любая формула, в которую аргумент 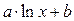 (где
(где  и
и 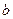 − некоторые числа), причем вся эта формула обязательно под интегралом должна делиться на
− некоторые числа), причем вся эта формула обязательно под интегралом должна делиться на 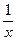 ). В этом случае рекомендуется замена переменной в интеграле по формуле
). В этом случае рекомендуется замена переменной в интеграле по формуле 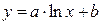 (так новая переменная
(так новая переменная 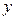 :
: 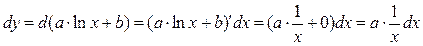 . Таким образом,
. Таким образом,  , откуда
, откуда 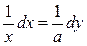 . Поэтому при замене переменной в интеграле вида
. Поэтому при замене переменной в интеграле вида  ) при указанной замене
) при указанной замене 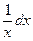 заменяется на
заменяется на 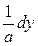 . Оформляется это следующей записью:
. Оформляется это следующей записью: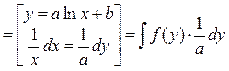 .
.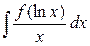 (т.е. при
(т.е. при  ) формула (1) переходит в более простую:
) формула (1) переходит в более простую: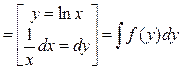 .
. .
.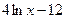 и есть
и есть 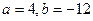 ):
): 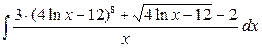
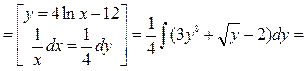
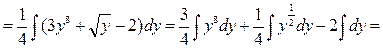 { остались интегралы из простой таблицы, только переменная интегрирования теперь обозначена не
{ остались интегралы из простой таблицы, только переменная интегрирования теперь обозначена не 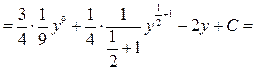
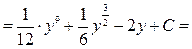 { возвращаемся в полученном ответе к старой переменной
{ возвращаемся в полученном ответе к старой переменной 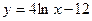 }=
}= 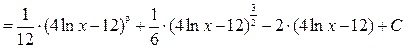 . Окончательно:
. Окончательно: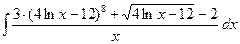
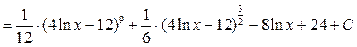 .
.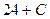 одной буквой
одной буквой 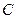 − от этого все множество соответствующих первообразных не изменилось бы.
− от этого все множество соответствующих первообразных не изменилось бы.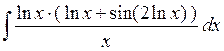 .
.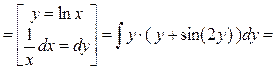
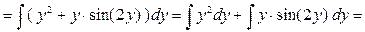 { первый интеграл – табличный, а для вычисления второго воспользуемся результатом примера 2 предыдущего параграфа
{ первый интеграл – табличный, а для вычисления второго воспользуемся результатом примера 2 предыдущего параграфа 
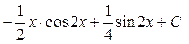 , заменив, естественно,
, заменив, естественно, 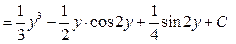 ={ возвращаемся в полученном ответе к старой переменной
={ возвращаемся в полученном ответе к старой переменной  }
} 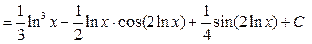 . Итак,
. Итак, 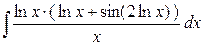
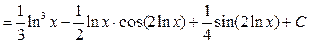 .
.


