
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение и вычисление определенного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим функцию f (x), определенную на промежутке [ a, b ]. Разо-бьем промежуток на п произвольных частей точками
и обозначим
На каждом промежутке
называется интегральной суммой функции f (x). Если при
Из приведенного определения естественно следует геометрический смысл определенного интеграла: если f (x) > 0, то Порядок выполнения работы Задание1. Вычислить значение интеграла от линейной функции, определить площадь соответствующей фигуры, записать выражения для инте-гральных сумм (при разбиении отрезка интегрирования на N равных частей длины
Указание. Для того чтобы вычислить определенный интеграл, щелкните в панели выделите выражение, щелкните по кнопке
и имя соответствующей интегральной суммы, выделите выражение предела, щелкните по кнопке Видно, что, когда длина отрезка разбиения стремится к нулю, значения интеграль-ных сумм стремятся к точному значению определенного интеграла. Ниже приведен фрагмент рабочего документа Mathcad
Значения подынтегральной функции вычисляются в левых концах отрезков
Значения подынтегральной функции вычисляются в правых концах отрезков
Значения подынтегральной функции вычисляются в серединах отрезков
Задание 2. Для заданной функции исследуйте поведение интегральных сумм на заданном отрезке интегрирования, разбивая отрезок интегрирования на равные части. Вычислите определенный интеграл и сравните его значение со значениями пределов интегральных сумм. Порядок выполнения задания 1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали. 2. Определите подынтегральную функцию как функцию переменной х и постройте ее график. 3. Вычислите определенный интеграл. 4. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в левом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.
6. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в середине отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.
7. Сравните полученные значения пределов между собой и со значением интеграла. 8. Постройте графики интегральных сумм как функций числа разбиений отрезка интегрирования. 9. Постройте графики интегральных сумм как функций длины отрезка разбиений. Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа. Индивидуальное задание к лабораторной работе 10. Вычислить определенный интеграл
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 13. Перечислите основные возможности символьной математики. 14. Каким образом можно задать упрощение выражения? 15. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 16. Каким образом можно выполнить разложение по степеням переменной? 17. Каким образом можно найти неопределеный интеграл от выражения? 18. Каким образом можно решить уравнение? Литература: 11. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 12. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 13. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 14. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 15. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с. Лабораторная работа №16
Цель работы: Освоить программирование в MathCad'е. Начальные сведения: Все элементы программирования находятся на рабочей панели Programming (Программирование):
Всего их десять: 1. AddLine – добавляет специальный программный блок, или добавляет еще одну линию в уже существующем программном блоке (рис 1.).
Рис. 1. Простейший программный блок. 2. ← - оператор присваивания (используется вместо ”:=” в программном блоке). Например, если требуется присвоить переменной N значение 10, то в программном блоке эта запись будет выглядеть следующим образом: N←10 (см. рис. 2).
Рис. 2. Использование оператора присваивания в программном блоке. 3. If (если) – оператор условия, используется для проверки некого условия и в зависимости от результата выполняет или не выполняет заданное действие (рис 3).
Рис. 3. Использование оператора условия If. 4. Otherwise (в противном случае) – оператор, который используется совместно с оператором If в случае, когда требуется выполнить действие при условии что выражение указанное в операторе If не является истинным. (рис. 4).
Рис. 4. Использование оператора Otherwise совместно с оператором If.
5. For – оператор цикла с переменной. Цикл продолжается до тех пор, пока значение переменной находится в заданном диапазоне значений. На каждом шаге цикла значение переменной автоматически увеличивается (или уменьшается, в зависимости от того, как указан диапазон изменения переменной) (см. рис 5).
Рис. 5. Примеры использования оператора For. 6. While – оператор цикла с условием. Цикл продолжается до тех пор, пока условие, указанное в операторе While истинно. (рис. 6).
Рис. 6. Примеры использования оператора While. 7. Break – оператор прерывания цикла. Если это оператор выполнится в теле цикла, то произойдет моментальное его завершение, операторы, которые находятся ниже Break, выполнены не будут (рис. 7).
Рис. 7. Пример использования оператора Break 8. Continue – оператор перехода к следующему шагу цикла. Если это оператор выполнится в теле цикла, то произойдет переход к следующему его шагу, операторы, которые находятся ниже Continue, выполнены не будут (рис. 8).
Рис. 8. Пример использования оператора Continue
9. Return – оператор возврата значения. Если это оператор выполнится в программе, то произойдет выход из программы, а также передача значения, указанного в Return, операторы, которые находятся ниже Return, выполнены не будут (рис. 9).
Рис. 9. Пример использования операторов Return и On Error 10. On Error – оператор обработки события возникновения ошибки. Работает аналогично оператору If. Если в выражении, которое записано справа от оператора On Error, возникает ошибка, то выполняется действие, записанное слева от оператора On Error. Пример обработки ошибки «Деление на ноль» представлен на рисунке 9.
Создайте новый документ MathCAD и выполните следующие задания:
Задание 1. Используя программный блок, напишите функцию, которая будет возвращать значение вида: “This number is negative”, в случае, если переданное ей число отрицательное, и “This number is positive”, если число положительное. Если переданное в качестве параметра функции число равно нулю, то функция должна вернуть значение “This number is NULL”
Используя программный блок, напишите функцию нахождения максимального числа из трех заданных. Задание 3. Используя программный блок, напишите функцию вычисления факториала по приведенному ниже алгоритму:
Используя программный блок и приведенный ниже пример, напишите функцию работы с матрицами согласно вашему варианту. Пример функции транспонирования матрицы:
ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ РАБОТЫ:
Примечание:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.246.21 (0.013 с.) |

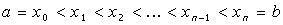
 .
. возьмем произвольную точку x i и вычислим в ней значение функции f(x). Выражение
возьмем произвольную точку x i и вычислим в ней значение функции f(x). Выражение
 существует и конечен предел
существует и конечен предел  , не зависящий ни от способа разбиения промежутка [ а, b ] точками
, не зависящий ни от способа разбиения промежутка [ а, b ] точками 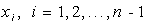 , ни от выбора точек
, ни от выбора точек  , то этот предел называют определенным интегралом от функции f (x) по промежутку [ a, b ], a саму функцию - интегрируемой на [ a, b ]. Обозначают
, то этот предел называют определенным интегралом от функции f (x) по промежутку [ a, b ], a саму функцию - интегрируемой на [ a, b ]. Обозначают
 равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми x = a, x = b.
равен площади фигуры, ограниченной графиком функции, осью абсцисс и прямыми x = a, x = b.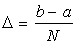 ), найти пределы интегральных сумм и по-строить графики зависимости интегральных сумм от N и от D.
), найти пределы интегральных сумм и по-строить графики зависимости интегральных сумм от N и от D. f (x):=2 х + 1 а:= 1 b:= 5
f (x):=2 х + 1 а:= 1 b:= 5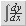 по кнопке
по кнопке  и введите с клавиатуры в помеченных позициях пре-делы интегрирования, подынтегральную функцию и переменную интегрирования;
и введите с клавиатуры в помеченных позициях пре-делы интегрирования, подынтегральную функцию и переменную интегрирования; в панели
в панели  , а затем по ра-бочему документу вне выделяющей рамки. Вычисленное значение интеграла будет отображено в рабочем документе справа от стрелки. Постройте график функции. Геометрическая фигура, ограниченная графиком функции, осью абсцисс и прямы-ми x = а, x = b, трапеция. Вычислите площадь трапеции и сравните со значением интеграла. Разбейте отрезок [ a, b ] на N равных частей и определите три интеграль-ные суммы как функции N, различающиеся способом выбора точки
, а затем по ра-бочему документу вне выделяющей рамки. Вычисленное значение интеграла будет отображено в рабочем документе справа от стрелки. Постройте график функции. Геометрическая фигура, ограниченная графиком функции, осью абсцисс и прямы-ми x = а, x = b, трапеция. Вычислите площадь трапеции и сравните со значением интеграла. Разбейте отрезок [ a, b ] на N равных частей и определите три интеграль-ные суммы как функции N, различающиеся способом выбора точки  на отрезке
на отрезке  : SI (N) для
: SI (N) для 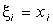 , Sr (N) для
, Sr (N) для  и Sm (N) для
и Sm (N) для 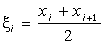 . Чтобы определить соответствующую интегральную сумму, введите с клавиатуры ее имя и знак присваивания; щелкните по кнопке
. Чтобы определить соответствующую интегральную сумму, введите с клавиатуры ее имя и знак присваивания; щелкните по кнопке  в панели
в панели  и введите в помеченных позициях индекс суммирования, его начальное и конечное значения и выражение для вычисления слагаемого. Чтобы найти предел интегральной суммы при
и введите в помеченных позициях индекс суммирования, его начальное и конечное значения и выражение для вычисления слагаемого. Чтобы найти предел интегральной суммы при  , щелкните по кнопке
, щелкните по кнопке  в панели
в панели  в панели
в панели  .
.





 5. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в правом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.
5. Запишите выражение для интегральной суммы, полученной при разбиении отрезка интегрирования на равные части, когда значение функции вычисляется в правом конце отрезка разбиения. Найдите ее предел при числе отрезков разбиения, стремящемся к бесконечности.

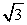 ]
]


 ]
]





 ]
]


 ]
]
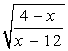









 Расчёты с помощью математической системы MathCAD.
Расчёты с помощью математической системы MathCAD.

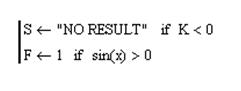








 Задание 2.
Задание 2.
 Задание 4.
Задание 4.
 12
12



