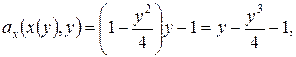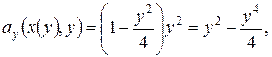Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычислить криволинейный интеграл I рода по дуге L.
Кафедра «Высшая математика»
Криволинейные интегралы
Методические указания
Волгоград УДК 517.373(075)
Рецензент: старший преподаватель кафедры «Прикладная математика» Н.И. Кольцова
Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета
Криволинейные интегралы: метод. указания / сост. М.И.Андреева, О.Е. Григорьева; ВолгГТУ. – Волгоград, 2011. – 26 с.
Методические указания являются руководством к выполнению индивидуальных заданий по теме «Криволинейные интегралы и их приложения к теории поля». В первой части методических указаний содержится необходимый теоретический материал для выполнения индивидуальных заданий. Во второй части рассмотрены примеры выполнения всех типов заданий, включенных в индивидуальные задания по теме, что способствует лучшей организации самостоятельной работы студентов и успешному усвоению темы. Методические указания предназначены для студентов первого и второго курсов.
© Волгоградский государственный технический университет, 2011
Определение криволинейного интеграла 1 рода Пусть È АВ – дуга плоской или пространственной кусочно-гладкой кривой L, f (P) – заданная на этой дуге непрерывная функция, А 0 = А, А 1, А 2, …, Аn – 1, Аn = B – произвольное разбиение дуги АВ и Pi – произвольные точки на частичных дугах È Аi – 1 Ai, длины которых D li (i = 1, 2, …, n). Тогда существует предел последовательности интегральных сумм
при n ® ¥ и max D li ® 0, который не зависит ни от способа разбиения дуги È АВ точками Ai, ни от выбора точек Pi на частичных дугах È Аi – 1 Ai (i = 1, 2, …, n). Этот предел называется криволинейным интегралом 1 рода от функции f (P) по кривой L и обозначается
Вычисление криволинейного интеграла 1 рода
Вычисление криволинейного интеграла 1 рода может быть сведено к вычислению определенного интеграла при разных способах задания кривой интегрирования.
Параметрическое задание кривой интегрирования
Если дуга È АВ плоской кривой задана параметрически уравнениями
где Аналогичная формула имеет место в случае параметрического задания пространственной кривой L. Если дуга È АВ кривой L задана уравнениями
где
Явное задание плоской кривой интегрирования в декартовых координатах
Если дуга È АВ плоской кривой L задана уравнением
и формула для вычисления криволинейного интеграла имеет вид:
При задании дуги È АВ плоской кривой L в виде x = x (y), y Î [ y 1; y 2],
и криволинейный интеграл вычисляется по формуле
Задание кривой интегрирования полярным уравнением
Если плоская кривая L задана уравнением в полярной системе координат r = r (j), j Î [j1; j2], где r (j) – непрерывно дифференцируемая функция, то
Приложения криволинейного интеграла 1 рода
С помощью криволинейного интеграла 1 рода вычисляются: длина дуги кривой, площадь части цилиндрической поверхности, масса, статические моменты, моменты инерции и координаты центра тяжести материальной кривой с заданной линейной плотностью. 1. Длина l плоской или пространственной кривой L находится по формуле
2. Площадь части цилиндрической поверхности с параллельной оси OZ образующей и расположенной в плоскости XOY направляющей L, заключенной между плоскостью XOY и поверхностью, задаваемой уравнением z = f (x; y) (f (P) ³ 0 при P Î L), равна
3. Масса m материальной кривой L с линейной плотностью m(P) определяется формулой
4. Статические моменты относительно осей Ox и Oy и координаты центра тяжести плоской материальной кривой L с линейной плотностью m(x; y) соответственно равны:
5. Статические моменты относительно плоскостей Oxy, Oxz, Oyz и координаты центра тяжести пространственной материальной кривой с линейной плотностью m(x; y; z) определяются по формулам:
6. Для плоской материальной кривой L с линейной плотностью m(x; y) моменты инерции относительно осей Ox, Oy и начала координат соответственно равны:
7. Моменты инерции пространственной материальной кривой L с линейной плотностью m(x; y; z) относительно координатных плоскостей вычисляются по формулам
а моменты инерции относительно координатных осей равны:
2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2 РОДА
Определение криволинейного интеграла 2 рода Пусть È АВ – дуга кусочно-гладкой ориентированной кривой L,
при n ® ¥ и max ÷
В случае, когда векторная функция
При изменении направления интегрирования криволинейный интеграл 2 рода меняет знак. Криволинейные интегралы первого и второго рода связаны соотношением
где С помощью криволинейного интеграла 2 рода можно вычислять работу силы
Положительным направлением обхода замкнутой кривой С, ограничивающей односвязную область G, считается обход против часовой стрелки. Криволинейный интеграл 2 рода по замкнутой кривой С называется циркуляцией и обозначается
Вычисление криволинейного интеграла 2 рода
Вычисление криволинейного интеграла 2 рода сводится к вычислению определенного интеграла.
Параметрическое задание кривой интегрирования
Если È АВ ориентированной плоской кривой задана параметрически уравнениями
Аналогичная формула имеет место в случае параметрического задания пространственной ориентированной кривой L. Если дуга È АВ кривой L задана уравнениями
Явное задание плоской кривой интегрирования
Если дуга È АВ плоской ориентированной кривой L задана в декартовых координатах уравнением
При задании дуги È АВ плоской ориентированной кривой L в виде
Пусть функции
в плоской замкнутой области G, ограниченной кусочно-гладкой замкнутой самонепересекающейся положительно ориентированной кривой С +. Тогда имеет место формула Грина:
Пусть G – поверхностно-односвязная область, и
– заданное в этой области векторное поле. Поле
где
Необходимое и достаточное условие потенциальности векторного поля rot
Если векторное поле
где М 0 М – произвольная кривая, соединяющая фиксированную точку М 0 и переменную точку М. Для упрощения вычислений в качестве пути интегрирования может быть выбрана ломаная М 0 М 1 М 2 М со звеньями, параллельными координатным осям, например:
Рис. 1 Тогда
3. примеры выполнения заданий Задание 1 Вычислить криволинейный интеграл I рода где L – дуга кривой Решение. По формуле (1.3) сведения криволинейного интеграла I рода к определенному интегралу в случае гладкой плоской явно заданной кривой:
где y = y (x), x 0 ≤ x ≤ x 1 – уравнение дуги L кривой интегрирования. В рассматриваемом примере
и дифференциал длины дуги кривой L
Так как
то, подставляя в это выражение
Преобразуем криволинейный интеграл к определенному:
Вычисляем этот интеграл с помощью подстановки
Задание 2 Вычислить криволинейный интеграл 1 рода Решение. Так как L – дуга гладкой плоской кривой, заданной в параметрическом виде, то используем формулу (1.1) сведения криволинейного интеграла 1 рода к определенному:
В рассматриваемом примере
Найдем дифференциал длины дуги
Найденные выражения подставляем в формулу (1.1) и вычисляем:
Задание 3 Найти массу дуги линии L с линейной плоскостью m. L: Решение. Масса m дуги L с плотностью m(P) вычисляется по формуле (1.8)
Это криволинейный интеграл 1 рода по параметрически заданной гладкой дуге кривой в пространстве, поэтому он вычисляется по формуле (1.2) сведения криволинейного интеграла 1 рода к определенному интегралу:
Найдем производные
и дифференциал длины дуги
Задание 4 Пример 1. Вычислить криволинейный интеграл 2 рода
по дуге L кривой 4 x + y 2 = 4 от точки A (1; 0) до точки B (0; 2). Решение. Плоская дуга L задана в неявном виде. Для вычисления интеграла удобнее выразить x через y:
и находить интеграл по формуле (2.8) преобразования криволинейного интеграла 2 рода в определенный интеграл по переменной y:
где ax (x; y) = xy – 1, ay (x; y) = xy 2. С учетом задания кривой
По формуле (2.8) получаем
Пример 2. Вычислить криволинейный интеграл 2 рода
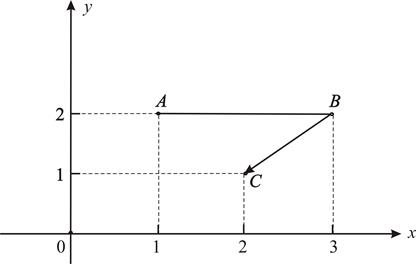
где L – ломаная ABC, A (1; 2), B (3; 2), C (2; 1). Решение. По свойству аддитивности криволинейного интеграла
Каждый из интегралов- слагаемых вычисляем по формуле (2.7)
где ax (x; y) = x 2+ y, ay (x; y) = –3 xy.
Рис. 2 Уравнение отрезка прямой AB: y = 2, y ¢ = 0, x 1 = 1, x 2 = 3. Подставляя в формулу (2.7) эти выражения, получаем:
Для вычисления интеграла
составим уравнение прямой BC по формуле
где xB, yB, xC, yC – координаты точек B и С. Получаем
Подставляем полученные выражения в формулу (2.7):
Задание 5 Вычислить криволинейный интеграл 2 рода по дуге L
Решение. Так как кривая интегрирования задана параметрически уравнениями x = x (t), y = y (t), t Î [ t 1; t 2], где x (t) и y (t) – непрерывно дифференцируемые функции t при t Î [ t 1; t 2], то для вычисления криволинейного интеграла второго рода используем формулу (2.5) сведения криволинейного интеграла к определенному для плоской параметрически заданной кривой
В рассматриваемом примере ax (x; y) = y; ay (x; y) = –2 x. C учетом задания кривой L получаем:
Подставляем найденные выражения в формулу (2.5) и вычисляем определенный интеграл:
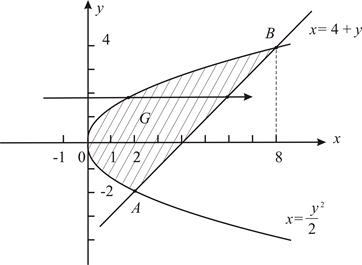
Задание 6 Пример 1. Вычислить криволинейный интеграл 2 рода по замкнутому контуру C + Решение. Обозначение C + указывает, что обход контура осуществляется в положительном направлении, то есть против часовой стрелки. Проверим, что для решения задачи можно использовать формулу Грина (2.9)
Так как функции ax (x; y) = 2 y – x 2; ay (x; y) = 3 x + y и их частные производные
Для вычисления двойного интеграла изобразим область G, предварительно определив точки пересечения дуг кривых y 2 = 2 x и Точки пересечения найдем, решив систему уравнений:
Второе уравнение системы равносильно уравнению x 2 – 10 x + 16 = 0, откуда x 1 = 2, x 2 = 8, y 1 = –2, y 2 = 4. Итак, точки пересечения кривых: A (2; –2), B (8; 4).
Рис. 3 Так как область G – правильная в направлении оси Ox, то для сведения двойного интеграла к повторному спроектируем область G на ось OY и воспользуемся формулой
Так как a = –2, b = 4,
Пример 2. Вычислить криволинейный интеграл 2 рода по замкнутому контуру Решение. Обозначение
Изобразим область G, ограниченную заданным контуром.
Рис. 4 Функции
Область G не является правильной в направлении какой-либо из осей. Проведем отрезок прямой x = 1 и представим G в виде G = G 1 È G 2, где G 1 и G 2 области, правильные в направлении оси Oy. Тогда Для сведения каждого из двойных интегралов по G 1 и G 2 к повторному будем использовать формулу
где [ a; b ] – проекция области D на ось Ox, y = y 1(x) – уравнение нижней ограничивающей кривой, y = y 2(x) – уравнение верхней ограничивающей кривой. Запишем уравнения границ области G 1 и найдем AB: y = 2 x, 0 ≤ x ≤ 1; AD:
Составим уравнение границы BC области G 2, используя формулу
BC: DC: Тогда
Итак,
Задание 7 Пример 1. Найти работу силы Решение. Работу переменной силы Так как векторная функция
В рассматриваемом примере y = x 3,
Пример 2. Найти работу силы Решение. Используя формулу (2.3), получаем
Рис. 5 В рассматриваемом примере дуга кривой L (È MN) – это четверть окружности, задаваемой каноническим уравнением x 2 + y 2 = 4. Для вычисления криволинейного интеграла второго рода удобнее перейти к параметрическому заданию окружности: x = R cos t, y = R sin t и воспользоваться формулой (2.5)
Так как x = 2cos t, y = 2sin t,
Задание 8 Пример 1. Вычислить модуль циркуляции векторного поля Решение. Для вычисления циркуляции векторного поля
Так как задано пространственное векторное поле
Кривая Г задана как пересечение двух поверхностей: гиперболического параболоида z = x 2 – y 2 + 2 и цилиндра x 2 + y 2 = 1. Для вычисления криволинейного интеграла удобно перейти к параметрическим уравнениям кривой Г. Уравнение цилиндрической поверхности можно записать в виде: Так как входящие в параметрические уравнения кривой Г функции
Учитывая, что
так как cos 4p = cos 0 = 1, sin 8p = sin 0 = 0.
Пример 2. Вычислить модуль циркуляции векторного поля Решение. Если одна из поверхностей, при пересечении которых образуется замкнутый контур Г, представляет собой плоскость, параллельную одной из координатных плоскостей, то циркуляцию удобно находить, используя формулу Стокса:
где S – часть двухсторонней поверхности, ограниченной замкнутым контуром Г, Находим ротор векторного поля
В качестве S выбираем верхнюю сторону плоскости z = 1. Тогда
По формуле Стокса получаем
где S – площадь части поверхности S, ограниченной контуром Г. Кривая Г задана как пересечение поверхности эллиптического параболоида
Как известно, площадь эллипса, задаваемого каноническим уравнением
Задание 9 Доказать, что векторное поле Решение. Докажем, что векторное поле потенциально, используя необходимое и достаточное условие потенциальности векторного поля
Найдем
Так как
Заданное векторное поле потенциально. Находим потенциал поля
Выбор точки M 0(x 0; y 0; z 0) определяется двумя условиями: 1) в точке M 0 векторное поле должно быть определено; 2) интегралы, входящие в формулу (2.13) должны максимально упрощаться. В данном случае выбираем в качестве M 0 начало координат.
3. примеры выполнения заданий Задание 1 Вычислить криволинейный интеграл I рода где L – дуга кривой Решение. По формуле сведения криволинейного интеграла I рода к определенному интегралу в случае плоской явно заданной кривой (1.3) имеем:
где y = y (x), x 0 ≤ x ≤ x 1 – уравнение дуги L кривой интегрирования. В нашем рассматриваемом примере
и дифференциал кривой L
Так как
то, подставляя в это выражение
и преобразуем криволинейный интеграл к определенному:
Вычисляем этот интеграл с помощью подстановки
Задание 2 Вычислить криволинейный интеграл 1 рода Решение. Так как L – дуга плоской кривой, заданной в параметрическом виде, то используем формулу (1.1) сведения криволинейного интеграла 1 рода к определенному:
Здесь
Найдем дифференциал длины дуги
Найденные выражения подставляем в данный интеграл и вычисляем:
Задание 3 Найти массу дуги линии L линейной плоскостью m. L: Решение. Масса М дуги L с плотностью z вычисляется по формуле (1.8)
В этом задании m = z, поэтому
Это криволинейный интеграл 1 рода по параметрически заданной дуге в пространстве, поэтому он вычисляется по формуле (1.2) сведения криволинейного интеграла 1 рода к определенному интегралу:
Найдем производные
Задание 4 Пример 1. Вычислить криволинейный интеграл 2 рода
по дуге L кривой 4 x + y 2 = 4 от точки A (1, 0) до точки B (0, 2). Решение. Плоская дуга L задана в неявном виде. Для вычисления интеграла удобнее выразить x через y:
и вычислять по формуле (2.8) преобразования криволинейного интеграла 2 рода в определенный интеграл по переменной y:
где ax (x, y) = xy – 1, ay (x, y) = xy 2. Теперь запишем
Далее подставляем эти выражения в данный криволинейный интеграл и преобразуем его в определе
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3838; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.66.242 (0.01 с.) |


 или
или  .
. где x (t) и y (t) – непрерывно дифференцируемые функции параметра t, причем x (t 1) = xA, x (t 2) = xB, то
где x (t) и y (t) – непрерывно дифференцируемые функции параметра t, причем x (t 1) = xA, x (t 2) = xB, то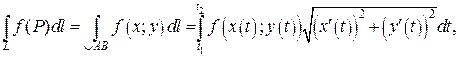 (1.1)
(1.1) - дифференциал длины дуги кривой.
- дифференциал длины дуги кривой. , и x (t), y (t), z (t) – непрерывно дифференцируемые функции параметра t, то
, и x (t), y (t), z (t) – непрерывно дифференцируемые функции параметра t, то (1.2)
(1.2) - дифференциал длины дуги кривой.
- дифференциал длины дуги кривой. где y (x) – непрерывно дифференцируемая функция, то
где y (x) – непрерывно дифференцируемая функция, то
 (1.3)
(1.3)
 (1.4)
(1.4) и
и (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8)
 (1.9)
(1.9)
 (1.10)
(1.10)
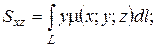
 (1.11)
(1.11)

 (1.12)
(1.12)

 (1.13)
(1.13)

 (1.14)
(1.14)

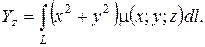 (1.15)
(1.15) = (ax (P); ay (P); az (P)) – заданная на этой дуге непрерывная векторная функция, А 0 = А, А 1, А 2, …, Аn – 1, Аn = B – произвольное разбиение дуги АВ и Pi – произвольные точки на частичных дугах Аi – 1 Ai. Пусть
= (ax (P); ay (P); az (P)) – заданная на этой дуге непрерывная векторная функция, А 0 = А, А 1, А 2, …, Аn – 1, Аn = B – произвольное разбиение дуги АВ и Pi – произвольные точки на частичных дугах Аi – 1 Ai. Пусть  – вектор с координатами D xi, D yi, D zi (i = 1, 2, …, n), и
– вектор с координатами D xi, D yi, D zi (i = 1, 2, …, n), и  – скалярное произведение векторов
– скалярное произведение векторов  и
и  (i = 1, 2, …, n). Тогда существует предел последовательности интегральных сумм
(i = 1, 2, …, n). Тогда существует предел последовательности интегральных сумм
 (P) по кривой L и обозначается
(P) по кривой L и обозначается (2.1)
(2.1) задана на плоской кривой L, аналогично имеем:
задана на плоской кривой L, аналогично имеем:
 (2.2)
(2.2) – единичный вектор касательной к ориентированной кривой.
– единичный вектор касательной к ориентированной кривой. при перемещении материальной точки по дуге кривой L:
при перемещении материальной точки по дуге кривой L: (2.3)
(2.3) (2.4)
(2.4) , где х (t) и y (t) – непрерывно дифференцируемые функции параметра t, причем
, где х (t) и y (t) – непрерывно дифференцируемые функции параметра t, причем  то
то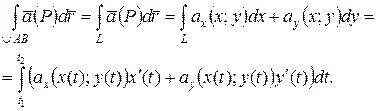 (2.5)
(2.5) – непрерывно дифференцируемые функции параметра t, то
– непрерывно дифференцируемые функции параметра t, то (2.6)
(2.6) где y (x) – непрерывно дифференцируемая функция, то
где y (x) – непрерывно дифференцируемая функция, то (2.7)
(2.7) (2.8)
(2.8) непрерывны вместе со своими производными
непрерывны вместе со своими производными
 (2.9)
(2.9) .
. , где (2.10)
, где (2.10) (2.11)
(2.11) (2.12)
(2.12)
 (2.13)
(2.13)
 , 0 ≤ x ≤ 1.
, 0 ≤ x ≤ 1.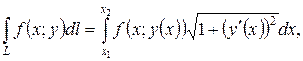
 Находим производную этой функции
Находим производную этой функции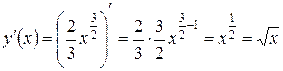
 .
. ,
, вместо y, получаем
вместо y, получаем
 .
. . Тогда
. Тогда  . После преобразований получаем
. После преобразований получаем
 по дуге L кривой L: x = cos 3 t, y = sin 3 t,
по дуге L кривой L: x = cos 3 t, y = sin 3 t,  .
. .
.

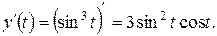



 .
.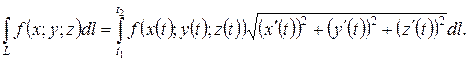



 Подставляем эти выражения в формулу для массы:
Подставляем эти выражения в формулу для массы: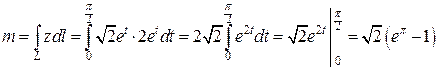 .
.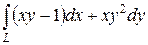
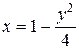







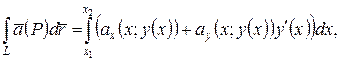

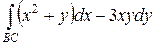

 y – 2 = x – 3, y = x – 1, y ¢ = 1.
y – 2 = x – 3, y = x – 1, y ¢ = 1.
 0 ≤ t ≤ 1.
0 ≤ t ≤ 1. .
.




 где С: y 2 = 2 x, y = x – 4.
где С: y 2 = 2 x, y = x – 4.
 непрерывны в плоской замкнутой области G, ограниченной контуром C, тоформула Грина применима.
непрерывны в плоской замкнутой области G, ограниченной контуром C, тоформула Грина применима. .
.
 .
.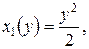 x 2(y) = 4+ y, то
x 2(y) = 4+ y, то

 где С – контур треугольника с вершинами A (0; 0), B (1; 2), C (3; 1).
где С – контур треугольника с вершинами A (0; 0), B (1; 2), C (3; 1).


 и частные производные
и частные производные  и
и  непрерывны в области G, поэтому можно применить формулу Грина. Тогда
непрерывны в области G, поэтому можно применить формулу Грина. Тогда



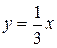 , 0 ≤ x ≤ 1.
, 0 ≤ x ≤ 1.

 где 1 ≤ x ≤ 3.
где 1 ≤ x ≤ 3. 1 ≤ x ≤ 3.
1 ≤ x ≤ 3.
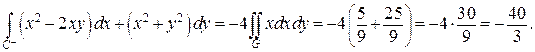
 при перемещении материальной точки вдоль линии L: y = x 3 от точки M (0; 0) к точке N (1; 1).
при перемещении материальной точки вдоль линии L: y = x 3 от точки M (0; 0) к точке N (1; 1). при перемещении материальной точки по дуге кривой L определяем по формуле (2.3) (как криволинейный интеграл второго рода от функции
при перемещении материальной точки по дуге кривой L определяем по формуле (2.3) (как криволинейный интеграл второго рода от функции  .
. и дуга
и дуга  плоской ориентированной кривой определена явно уравнением y = y (x), x Î [ x 1; x 2], где y (x) непрерывно дифференцируемая функция, то по формуле (2.7)
плоской ориентированной кривой определена явно уравнением y = y (x), x Î [ x 1; x 2], где y (x) непрерывно дифференцируемая функция, то по формуле (2.7) .
. , x 1 = xM = 0, x 2 = xN = 1. Поэтому
, x 1 = xM = 0, x 2 = xN = 1. Поэтому
 при перемещении материальной точки вдоль линии L: x 2 + y 2 = 4 от точки M (0; 2) к точке N (–2; 0).
при перемещении материальной точки вдоль линии L: x 2 + y 2 = 4 от точки M (0; 2) к точке N (–2; 0). .
.
 .
. ,
,  ,
, 
 получаем
получаем
 вдоль контура Г:
вдоль контура Г: 
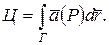
 .
.
 ,
,  ,
,  , а также тригонометрические формулы sin 2 t = 2sin t cos t,
, а также тригонометрические формулы sin 2 t = 2sin t cos t,  получаем
получаем
 вдоль контура
вдоль контура 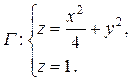

 – единичный вектор нормали к поверхности S, и выбор стороны поверхности и направление обхода контура Г согласованы.
– единичный вектор нормали к поверхности S, и выбор стороны поверхности и направление обхода контура Г согласованы.
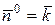 и скалярное произведение
и скалярное произведение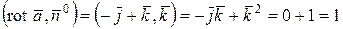 .
.
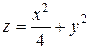 и плоскости z = 1, то есть представляет собой эллипс, расположенный в плоскости z = 1 и задаваемый уравнениями
и плоскости z = 1, то есть представляет собой эллипс, расположенный в плоскости z = 1 и задаваемый уравнениями
 вычисляется по формуле S = p ab. Поэтому
вычисляется по формуле S = p ab. Поэтому .
. потенциально. Найти потенциал поля.
потенциально. Найти потенциал поля. (2.10)
(2.10)
 по формуле (2.11)
по формуле (2.11) .
. , то
, то
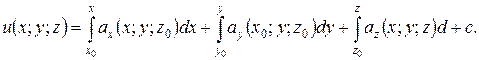





 ,
,
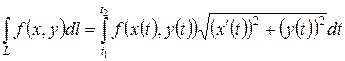 .
.

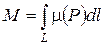 .
. .
.
 Подставим эти выражения в формулу для массы:
Подставим эти выражения в формулу для массы: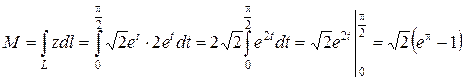 .
.