
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IX. Решить систему нелинейных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Указание. Введите с клавиатуры ключевое слово Given (дано), затем правее и ниже ключевого слова левую часть первого уравнения системы, далее сим-вольный знак равенства (нажмите на клавиатуре клавиши <Ctrl>+<=>) и правую часть уравнения (нуль). Аналогично введите остальные два уравнения системы. Правее и ниже последнего уравнения системы введите имя функции Find (найти), перечислите в скобках имена переменных, значения которых нужно вычислить, выделите Find(x,y,z), щелкните по кнопке Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа. Индивидуальные задания к работе 2 I.Упростить выражение:
II. Раскрыть скобки и привести подобные в выражении:
III. Разложить на множители выражение:
IV. Разложить на простые дроби рациональную дробь:
VIII. Решить систему уравнений:
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями.
Контрольные вопросы:
1. Что из себя представляет система MathCAD? 2. Каким образом осуществляется формулировка математических задач средствами MathCAD 11? 3. Как можно задать текстовый блок? 4. Что такое «ранжированная переменная»? 5. Каким образом осуществляется управлением форматом выводимых данных?
Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПО ФОРМУЛАМ КРАМЕРА Цель лабораторной работы - ознакомиться с основными правилами решения уравнений и систем уравнений численными методами и возможностями пакета MathCAD при построении графиков. Рассмотрим решение линейных систем по формулам Крамера. Пусть
cистема n линейных алгебраических уравнений относительно n неизвестных x1, x2,..., xn. Матрица называется матрицей системы, а вектор-столбец b = ( b1 b2... bn )T - столбцом правых частей системы. Рассмотренная система линейных алгебраических уравнений может быть записана в матричной форме в виде Ах = b, где х - вектор-столбец неизвестных, х = ( х1 x2... xn )T. Справедливо следующее утверждение. Если определитель D = det A матрицы системы Ах = b отличен от нуля, то система имеет единствен-ное решение x1, х2,..., xn, определяемое формулами Крамера хi = Порядок выполнения работы Задание. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы
Указание: 1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали.
2. Присвойте переменной ORIGIN значение, равное 1. 3. Введите матрицу и столбец правых частей. 4. Вычислите определитель матрицы. 5. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей. Указание. Для вычисления определителей D1, D2, D3, D4 проще всего скопировать матрицу А в буфер обмена (<Ctrl>+<C> или пункт Copy меню Edit), затем вставить в помеченной позиции матрицу из буфера обмена (<Ctrl>+<V> или пункт Insert меню Edit) и затем заменить элементы соответствующего столбца элементами столбца правых частей. 6.Найдите по формулам Крамера решение системы. Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Индивидуальные задания к лабораторной работе 3. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы Ах = B. 1. А = 2. A = 3. A = 4. A = 5. A = 6. A = 7. A =
9. A = 10. A = 11. A = 12. A = 13. A = 14. A = 15. A =
17. A = 18. A =
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Назовите основные способы решения систем линейных уравнений. 2. Какие операторы позволяют осуществить решение систем нелинейных уравнений? 3. Для чего необходимо выполнять проверку решения уравнений? 4. В чем смысл решения уравнений численными методами? 5. Назовите порядок построения графика в декартовых системах координат. 6. Назовите порядок построения графика в полярной системе координат. Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с. Лабораторная работа 4
Цель работы: Освоить работу с процессом символьных вычислений на примере вычисления интегралов, производных, сумм, пределов. Изучить работу с векторами и матрицами. Задание: 1. По заданным координатам точек A, B, C, D найти координаты векторов a=AB и b=CD. 2. Вычислить скалярное и векторное произведения найденных векторов. 3. Найти следующие произведения векторов на заданную матрицу M: a*M и M*b. 4. Вычислить определитель матрицы M. 5. Для заданного ряда вычислить i -частичную сумму и исследовать сходимость ряда. 6. Вычислить сумму ряда. 7. Найти первообразную неопределенного интеграла и выполнить проверку, полученного результата. 8. Вычислить значения определенного интеграла. Пример выполнения задания: Задание:
1. Для выполнения задания 1 используем известную формулу из курса линейной алгебры, которая гласит, что координаты вектора численно равны разности координат точек конца и начала вектора:
Для этого в MathCAD точки A, B, C и D набираются в следующем виде:
Для чего открываем панель инструментов «Математика» (View\Toolbars\Math) и нажимаем на ней кнопку «Матрицы» ([MMM])
Далее задаем параметр i, меняющийся от 0 до 2 (для чего на панели «Матрица» есть кнопка вида “ m..n”). Примечание. Отметим, что в пакете MathCAD нумерация компонент векторов и элементов матриц начинается с 0:
Для просмотра координат векторов достаточно набрать «a=» и «b=». В данной задаче
Рекомендация: предлагаем читателю самостоятельно вычислить в MathCAD длину полученных векторов. 2. Вычислим скалярное и векторное произведение полученных векторов. Примечание. Обращаем внимание на то, что вычисление скалярного произведения в MathCAD осуществляется согласно правилу умножения матриц. В связи с этим вектора следует задавать следующим образом:
Примечание. Верхний индекс Т у вектора а означает операцию транспонирования и является результатом работы кнопки MT на панели «Матрица». Вычислим скалярное произведение:
Проверим результат, воспользовавшись определением скалярного произведения:
или в виде
Примечание. Если вектор задан в строчку, то MathCAD воспринимает его не как вектор, а как матрицу с одной строкой и n столбцами. Для набора нижнего индекса можно нажимать на клавиатуре кнопку [.
В качестве примера продемонстрируем проверку антикоммутативности векторного произведения
3. Рассмотрим произведение матрицы на вектор. Матрица задается с помощью встроенных функций пользователя, а произведение ее на вектор в MathCAD имеет вид:
Умножение вектора на матрицу осуществляется следующим образом:
4. Вычисление определителя матрицы выполняется с помощью встроенной символьной операции 5. Частичные суммы рядов вычисляются с помощью определенных символьных операций, представленных на рис. 1.
Рис. 1 Результаты вычислений имеют вид:
Примечание. Из курса математического анализа известно, что частичные суммы в теории рядов представляют собой отправную точку в исследовании их сходимости. Средства MathCAD позволяют, используя фундаментальное определение сходимости числового ряда, рассмотреть этот вопрос для различных числовых рядов. Здесь в качестве примера мы рассматриваем заданный выше ряд.
6. Ряд сходится, следовательно, можно вычислить его сумму:
7. Для вычисления неопределенных интегралов также используются встроенные символьные вычисления (см. рис. 1).
Примечание. Отметим, что в полученном результате отсутствует аддитивная постоянная. Согласно основному свойству интегралов производная от первообразной должна быть равна подынтегральной функции. Часто это свойство используется в качестве проверки полученных первообразных. Для вычисления производных снова используем встроенные символьные вычисления (см. рис. 1). В нашем случае получаем:
8. Для вычисления определенного интеграла, используя символьные операции, получаем
Примечание. Возможности пакета позволяют с помощью указанных символьных операций проводить исследования сходимости несобственных интегралов и изучение поведения разрывных функций на заданном интервале. 1.
1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Назовите способы выполнения символьных операций в MathCAD. 2. Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме? 3. Перечислите символьные операции с выделенными выражениями. 4. Перечислите символьные операции с выделенными переменными. 5. Перечислите символьные операции с выделенными матрицами. 6. Перечислите символьные операции преобразования. 7. Какие параметры определяет стиль представления результатов вычислений и где он задается? 8. В каких случаях результат символьных преобразований помещается в буфер обмена? 9. Каким образом можно вычислить предел в MathCAD? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.147 (0.013 с.) |


 * При вводе с клавиатуры символа <;> в рабочем документе отображается символ, разделяющий границы диапазона <..>.
* При вводе с клавиатуры символа <;> в рабочем документе отображается символ, разделяющий границы диапазона <..>.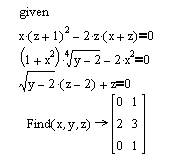
 в панели
в панели  . Вычисленное решение системы будет отображено после щелчка мышью вне выделяющей рамки в рабочем документе справа от стрелки в виде матрицы, каждый столбец кото-рой содержит одно из решений системы. В приведенном выше фрагменте рабочего документа найдены два решения системы: x=0,y=2,z=0 и x=l,y=3,z=l.
. Вычисленное решение системы будет отображено после щелчка мышью вне выделяющей рамки в рабочем документе справа от стрелки в виде матрицы, каждый столбец кото-рой содержит одно из решений системы. В приведенном выше фрагменте рабочего документа найдены два решения системы: x=0,y=2,z=0 и x=l,y=3,z=l.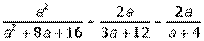
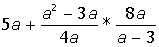

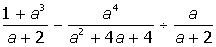
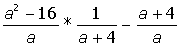
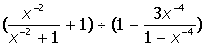
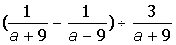
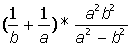
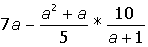
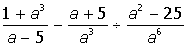
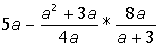
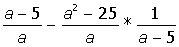
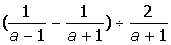
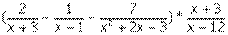


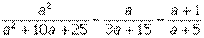
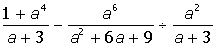

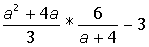

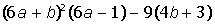
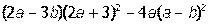
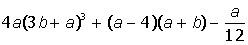
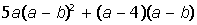
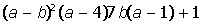
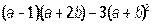
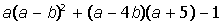
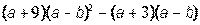

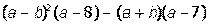
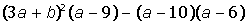
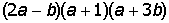
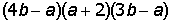
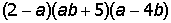


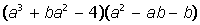
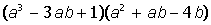

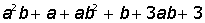
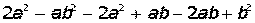
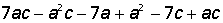
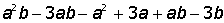

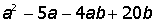
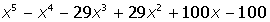
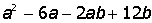
 5.
5.

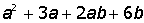
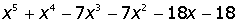
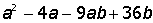

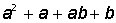
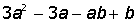
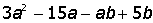
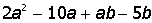
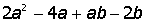
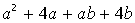
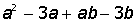
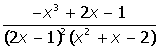
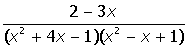
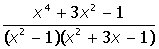
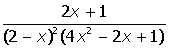
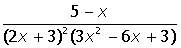

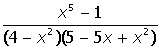
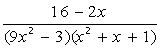
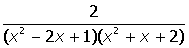


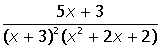
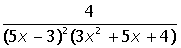
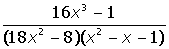
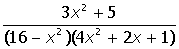
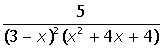
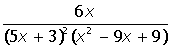
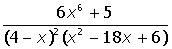
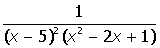
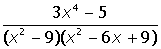
 VII. Решить символьное уравнение:
VII. Решить символьное уравнение: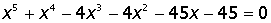

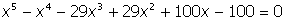

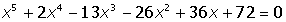
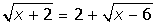
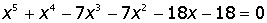

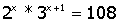
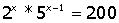
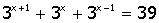

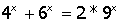
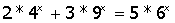
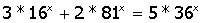

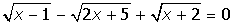
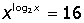
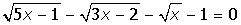

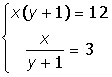
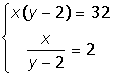
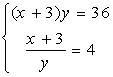
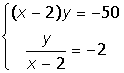
 3.
3.

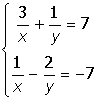
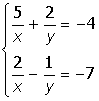
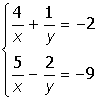
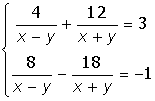
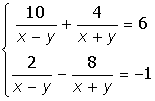
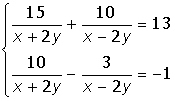
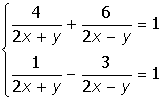
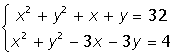
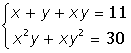

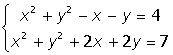

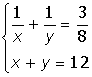
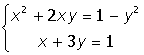
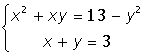

 Лабораторная работа 3
Лабораторная работа 3

 , где D i определитель матрицы n-го порядка, полученной из матрицы системы заменой i?го столбца столбцом правых частей.
, где D i определитель матрицы n-го порядка, полученной из матрицы системы заменой i?го столбца столбцом правых частей.



 B =
B = 
 B =
B = 
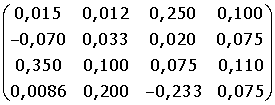 B =
B = 
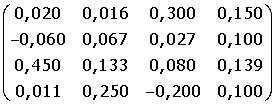 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 
 8. A =
8. A = 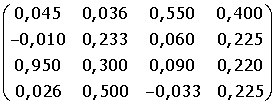 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 

 B =
B = 
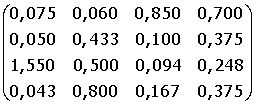 B =
B = 
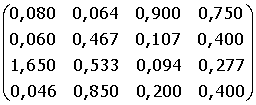 B =
B = 
 16. A =
16. A =  B =
B = 
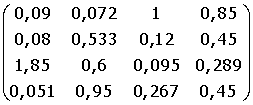 B =
B = 
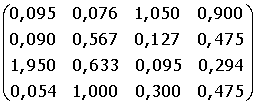 B =
B = 
 «Символьные вычисления»
«Символьные вычисления»


 . (1)
. (1)
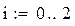
 Для нахождения координат наших векторов используем формулу (1), которая в MathCAD имеет вид:
Для нахождения координат наших векторов используем формулу (1), которая в MathCAD имеет вид:

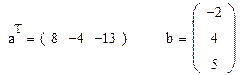

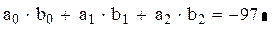
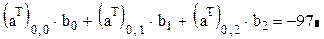
 Для вычисления векторного произведения вектора следует задавать в виде столбцов.
Для вычисления векторного произведения вектора следует задавать в виде столбцов.


 .
.








 2.
2.  при
при 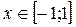
 Содержание отчета
Содержание отчета


