
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование заменой переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим функцию f (x), определенную на промежутке* (а, b). Дифференцируемая на промежутке (а, b) функция F (x), производная которой в каждой точке (а, b) равна f (x), называется первообразной функции f (x), если: F '(x) = f (x). Поскольку (F (x) + С)' = F '(x) = f (x) для любой постоянной С, то можно говорить о семействе первообразных множестве функций вида F (x) + C которое называется неопределенным интегралом функции f (x) и обозначается символом
где f (x) подынтегральная функция; х переменная интегрирования; F(x) + С значение неопределенного интеграла, т.е. семейство пер-вообразных функции f{x):
Порядок выполнения работы 1). Вычислите неопределенный интеграл Указание: 1. Установите автоматический режим вычислений и режим ото-бражения результатов вычислений по горизонтали. 2. Определите подынтегральную функцию как функцию пере-менной х. 3. Найдите первообразную, используя символьную математику пакета. 4. Определите первообразную как функцию переменной. 5. Найдите производную первообразной, используя символьную математику пакета. 6. Упростите производную от первообразной, сравните резуль-тат с подынтегральной функцией. 7. Постройте на одном графике изображения нескольких перво-образных.
Ниже приведен фрагмент рабочего документа Mathcad
Если j(t) непрерывно дифференцируемая функция, то, полагая x= j(t), получим формулу интегрирования заменой переменной:
Задание. Вычислите неопределенный интеграл Указание.
2. Скопируйте в рабочий документ подынтегральную функцию переменной х, скопируйте в буфер обмена выражение для х и выполните замену (выделите х, щелкните по строке Substitute в пункте Variable меню Symbolics).
3. Вычислите неопределенный интеграл по t, действуя как описано выше.
4. Выполните обратную подстановку (замените переменную t ее выражением через х).
5. Упростите выражение (разложите на множители), используя меню символьных операций Symbolics, пункт Factor.
6. Проведите проверку полученных результатов. Продифференцируйте полученное выражение по x и упростите. * Здесь возможно а = - бесконечность, b = + бесконечность * Выделите выражение, щелкнув вблизи него по полю и растянув пунктирный прямоугольник, и выберите в меню Edit пункт Copy либо нажмите комбинацию клавиш <Ctrl>+<C>. ** Выберите в меню Edit пункт Insert либо нажмите комбинацию клавиш <Ctrl>+<V>.
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа. Индивидуальны задания к лабораторной работе 9. Вычислите неопределенный интеграл
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 7. Перечислите основные возможности символьной математики. 8. Каким образом можно задать упрощение выражения? 9. 10. Каким образом можно выполнить разложение по степеням переменной? 11. Каким образом можно найти неопределеный интеграл от выражения? 12. Каким образом можно решить уравнение? Литература: 6. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 7. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 8. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 9. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 10. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 :
:
 - знак интеграла; f (x) dx подынтегральное выражение;
- знак интеграла; f (x) dx подынтегральное выражение;
 и проверьте правильность вычи-слений; постройте графики семейств первообразных.
и проверьте правильность вычи-слений; постройте графики семейств первообразных. Указание. Для того, чтобы вычислить неопределенный интеграл, щелкните по кнопке
Указание. Для того, чтобы вычислить неопределенный интеграл, щелкните по кнопке  в панели
в панели  , введите с клавиатуры в помеченных позициях по-дынтегральную функцию и переменную интегрирования, выделите все выражение рамкой, затем щелкните по кнопке
, введите с клавиатуры в помеченных позициях по-дынтегральную функцию и переменную интегрирования, выделите все выражение рамкой, затем щелкните по кнопке  в панели
в панели  . Первообразная, в которой по умолчанию значение произвольной константы равно нулю, будет отображена справа от стрелки. Скопируйте вычисленное выражение и присвойте его функции переменной х (в приведенном фрагменте - это F (x)). Для того чтобы проверить первообразную, вычислите ее производную. Для этого скопируйте в буфер обмена* выражение первообразной, щелкните по кнопке дифференцирования
. Первообразная, в которой по умолчанию значение произвольной константы равно нулю, будет отображена справа от стрелки. Скопируйте вычисленное выражение и присвойте его функции переменной х (в приведенном фрагменте - это F (x)). Для того чтобы проверить первообразную, вычислите ее производную. Для этого скопируйте в буфер обмена* выражение первообразной, щелкните по кнопке дифференцирования  , вставьте из буфера обмена** выражение первообразной, введите с клавиатуры переменную дифференцирования и дальше действуйте так же, как при символьном вычислении первообразной. Построить графики семейства первообразных можно, щелкнув по кнопке
, вставьте из буфера обмена** выражение первообразной, введите с клавиатуры переменную дифференцирования и дальше действуйте так же, как при символьном вычислении первообразной. Построить графики семейства первообразных можно, щелкнув по кнопке  в панели
в панели  . Далее следует ввести в помеченной позиции возле оси ординат, разделяя запятой, выражения для первообразных с различными значени-ями константы (в приведенном фрагменте это F (x) 5, 10, 15) и щелкнуть по рабочему документу вне поля графиков.
. Далее следует ввести в помеченной позиции возле оси ординат, разделяя запятой, выражения для первообразных с различными значени-ями константы (в приведенном фрагменте это F (x) 5, 10, 15) и щелкнуть по рабочему документу вне поля графиков.

 .
. заменой переменных.
заменой переменных. 1. Для того чтобы выполнить в неопределенном интеграле замену переменной х новой переменной
1. Для того чтобы выполнить в неопределенном интеграле замену переменной х новой переменной  , введите в рабочий документ
, введите в рабочий документ  и разрешите его относительно переменной х (выделите х, щелкните по строке Solve в пункте Variable меню Symbolics), затем продифференцируйте полученное выражение по t (т.е найдем d x).
и разрешите его относительно переменной х (выделите х, щелкните по строке Solve в пункте Variable меню Symbolics), затем продифференцируйте полученное выражение по t (т.е найдем d x).




















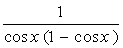





 Каким образом можно получить значение числа π с точностью 25 знаков после запятой?
Каким образом можно получить значение числа π с точностью 25 знаков после запятой? Лабораторная работа 15
Лабораторная работа 15


