
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разветвляющийся вычислительный процесс»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Познакомить читателя со встроенными возможностями пакета MathCAD для линейного программирования, а также для разветвляющегося вычислительного процесса. Рекомендуемая литература: [1–4, 7]. Задание: 1. Написать линейную программу для вычисления заданных параметров. 2. Написать программу с разветвляющимся вычислительным процессом, для вычисления функции с условием. Пример выполнения задания: Задание:
1. Для программирования в MathCAD имеется панель инструментов «Программирование»:
Рассмотрим имеющиеся на ней функции. – Add Line – создает и при необходимости удлиняет жирную вертикальную линию, с право от которой записывается программный блок; – – символ присваивания. Например: x 12 означает что переменной x присваивается значение 12; – if – условный оператор, записывается как: Выражение if условие, т.е. Выражение выполняется, если условие выполнено; – otherwise – инструкция «иначе» (в противном случае), обычно используется с оператором if, когда необходимо вернуть значение при невыполнении условия оператора if; – for – оператор цикла со счетчиком. Например: for счетчик Î N1.. N2; – while – оператор цикла с условием. Например: while условие; – break – инструкция прерывания; – continue – инструкция продолжения, позволяет вернуться в точку прерывания; – return – инструкция возврата, возвращает значение оператора, указанного после нее;
– on error – инструкция обработки ошибок, позволяет обрабатывать ошибки, например: Выражение_1 on error Выражение 2, если Выражение_1 содержит ошибку выполняется Выражение_2. Линейной программой называется вычислительный процесс, в котором все действия выполняются последовательно один за другим. При написании линейной программы никаких особых возможностей MathCAD не требуется. Для нашей задачи воспользуемся формулой Герона для нахождения площади:
При написании линейных вычислений важно соблюдать порядок действий. Сначала зададим стороны: а:=3.24 b:=4.23 с:=2.51 Прежде чем вычислять сумму, сначала необходимо найти полупериметр:
а затем площадь:
После того как все формулы введены, можно посмотреть результат, для этого наберем: S= и получим:
2. Воспользовавшись вышеуказанными операторами, сформируем функцию Z(x,y). Для этого набираем «Z(x,y):=» и выбираем инструкцию Add Line:
в верхнее поле ввода помещаем условный оператор if:
Заполняя поля условного оператора, получим:
Обращаем ваше внимание на то, что скобки в условном операторе обязательны. У нас остались значения, которые принимает функция при невыполнении заданного условия. Для учета этого воспользуемся инструкцией otherwise:
Таким образом, функция Z(x,y) сформирована и мы можем посмотреть ее значения в различных точках:
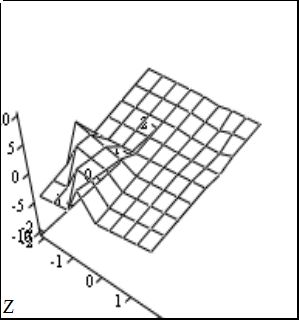
Построим поверхность полученной функции:
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
«Программирование в MathCAD. Циклы и подпрограммы» Цель работы: Познакомить читателя с более серьезными возможностями программирования в системе MathCAD. Рекомендуемая литература: [1-4, 7]. Задание: 1. С помощью циклического оператора вычислить 2. Вычислить сумму и произведение элементов ряда, лежащих в заданном интервале. 3. Написать блок вычисления суммы ряда и, воспользовавшись им как подпрограммой, вычислить абсолютную и относительную разницу между i- частичной суммой и суммой ряда. 4. Найти разброс i- частичных сумм относительно суммы ряда.
Пример выполнения задания: Задание:
1. Воспользуемся циклическим оператором for для вычисления элементов ряда. Для этого запишем «Т:=» и дважды вызовем инструкцию Add Line, получим:
где T – есть вектор элементов ряда. В первом поле ввода поместим оператор присваивания начального значения ряда:
Во втором поле поместим оператор цикла:
В последнем поле помещаем имя возвращаемого объекта:
2. Вычислим сумму элементов ряда, лежащих в заданном интервале. Для этого оформим сумму элементов ряда как функцию от a и b, где a и b – границы заданного интервала. Запишем основу для данного блока, как это делалось ранее:
Перед вычислением переменную, в которую будем насчитывать сумму ряда, необходимо обнулить:
Далее откроем цикл:
и в тело цикла вставим условный оператор:
Заканчиваем программный модуль и получаем:
Теперь мы можем вычислить сумму элементов ряда из любого интервала:
Сумму S можно вычислить иначе:
Но в таком случае мы получим только одно значение суммы элементов ряда из указанного интервала:
Рассмотрим вычисление произведения элементов ряда, попадающих в заданный интервал:
Ясно, что произведение элементов из интервала [-1; 0] будет нулевым за счет правого края интервала, но мы можем вычислить произведение из интервала, близкого к исходному, например [-1; -0.0001]:
3. Вычислим абсолютную и относительную разницу между i -частичной суммой и суммой ряда. Для этого оформим вычисление i- частичных сумм:
где Теперь можно вычислить абсолютную и относительную разницы:
Для проверки вычислим абсолютную и относительную разницы для всей суммы:
Построим графики абсолютных и относительных разностей:
Отметим, что для получения графика относительной ошибки умножили результат на 100 %. 4. Вычислим разброс i- частичных сумм относительно суммы ряда. Воспользуемся для этого уже созданным программным блоком для вычисления i- частичной суммы ряда. В результате получим:
среднее квадратичное отклонение равно:
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
«Методы решения дифференциальных уравнений и систем» Цель работы: Познакомить читателя со встроенными возможностями пакета MathCAD для решения дифференциальных уравнений (ДУ) и систем ДУ. Рекомендуемая литература: [1 – 10]. Задание: 1. По заданной правой части ДУ первого порядка с разделяющимися переменными построить решение при помощи встроенных функций MathCAD.
2. Построить разностную схему для ДУ из п. 1. 3. Сравнить полученные в п. 1 и 2 решения. 4. Найти общее решение линейного неоднородного ДУ первого порядка. 5. Сделать проверку найденного в п. 4 решения. 6. Найти решение неоднородного ДУ второго порядка с заданными начальными условиями. 7. Решить систему ДУ. Пример выполнения задания: Задание:
1. ДУ первого порядка с разделяющимися переменными можно представить как:
где y(x) – неизвестная функция, а функция f(x,y) – представляет собой неоднородную часть ДУ, которая здесь допускает представление f(x,y)=g(x)*h(y).
Далее записывается блок решения ДУ, который начинается командным словом Given и формируется при помощи панели инструментов «Булево»:
где Odesolve(x,x1)– встроенная функция пользователя, которая формирует решение ДУ, заданного командным блоком Given, x – переменная дифференцирования, x1 – конечное значение интервала интегрирования. 2. Для записи разностной схемы ДУ необходимо задать количество итераций N, итерационный параметр i и шаг по переменной интегрирования dx:
Наберем вектор значений переменной интегрирования и начальное значение искомого решения y 1:
Запишем разностную схему:
где вид правой части f(x,y) был задан выше. Получаем, что разностное решение имеет вид:
3. Сравним два полученных выше решения графически:
Из графика следует, что при уменьшении параметра N точность полученного в п. 2 решения будет ухудшаться, а при увеличении N – улучшаться. 4. Найдем решение неоднородного ДУ первого порядка, для этого запишем его в общем виде: y’=a(x)*y+b(x) и применим к нему готовую математическую формулу, которую можно найти в любой книге, посвященной решению обыкновенных ДУ [например 6]:
где С – константа интегрирования. Заметим, что у нас
Подставим начальное условие:
Теперь можно построить график:
5. Сделаем проверку полученного в п. 4 решения. Для этого подставим полученную функцию в исходное уравнение и воспользуемся символьной функцией simplify:
Как мы можем убедиться, полученный результат полностью совпадает с исходной правой частью. 6. Для решения неоднородного ДУ второго порядка, как и в п. 1, используются блок, начинающийся с командного слова Given,и встроенная функция пользователя Odesolve:
где x – аргумент функции, 6 – конечное значение аргумента, 100 – количество шагов. Для графического представления зададим x следующим образом
Тогда график y(x) примет вид:
7. Для решения системы ДУ зададим начальные значения и параметры: а:= –0.2 Далее зададим вектор правых частей, следующим образом:
Теперь воспользуемся функцией rkfixed:
где х – вектор начальных значений; 0 и 20 – интервал по времени, на котором производится поиск решения для данной системы ДУ; 100 – количество точек на интервале; D – вектор правых частей системы ДУ; Z – матрица решений данной системы уравнений, у которой количество столбцов равно количеству уравнений в системе, а количество строк задается количеством точек на интервале. Далее, если мы хотим построить график решений, то необходимо задать целочисленный параметр n для индексов матрицы решений: n:=0..99 Теперь можно строить график зависимости y (Zn,1) от x(Zn,0), получим:
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.161.95 (0.011 с.) |




 ,
, где
где .
.
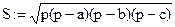







 ЛАБОРАТОРНАЯ РАБОТА № 10
ЛАБОРАТОРНАЯ РАБОТА № 10 T0=0
[-1; 0]
T0=0
[-1; 0]

















 – сумма всего ряда.
– сумма всего ряда.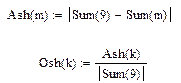






 ЛАБОРАТОРНАЯ РАБОТА № 11
ЛАБОРАТОРНАЯ РАБОТА № 11 y (0)=1
x Î[0; 2p]
y (0)=1
x Î[0; 2p]
 y (0)=1
y (0)=1
 y (0)=-8
y’ (0)=3
y (0)=-8
y’ (0)=3

 x (0)=0 y (0)=1 a =-0.2
x (0)=0 y (0)=1 a =-0.2

 Для решения данного ДУ нужно задать правую часть f(x,y), начальные условия и интервал изменения x,на котором следует найти решение:
Для решения данного ДУ нужно задать правую часть f(x,y), начальные условия и интервал изменения x,на котором следует найти решение:


 .
. ,
, .
.
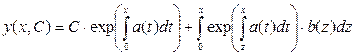 , (2)
, (2) и
и  запишем формулу (2) в MathCAD:
запишем формулу (2) в MathCAD: Получим следующий результат:
Получим следующий результат:

 Для графика полученного решения необходимо задать интервал изменения переменной x и шаг ее изменения:
Для графика полученного решения необходимо задать интервал изменения переменной x и шаг ее изменения: .
.
 .
.
 .
.



 ,
,
 Каким образом можно выполнить разложение по степеням переменной?
Каким образом можно выполнить разложение по степеням переменной? Лабораторная работа 12
Лабораторная работа 12


