
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложения кусочно-непрерывных функций в ряд Фурье.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для непрерывной периодической функции f (x) на отрезке [-p, p] можно поставить в соответствие ряд частичных сумм Фурье S (x): f (x)~ S (x). Вычисление частичных сумм ряда Фурье выполняют по формуле:
Цель работы. Исследовать графически поведение частичных сумм ряда Фурье заданного кусочно-непрерывной функцией f (x). Вычислить значение суммы ряда Фурье в указанных точках и на границах интервала -p, p. Задание. Построить график f(x). Построить графики частичных сумм для n = 1, 2, 5, 10, 50: S (x, 1), S (x, 2), S (x, 5), S (x, 10), S (x, 50)и сравнить их между собой и с графиком f (x). Для x = p / 2 (точка непрерывности) построить график частичной суммы S (p / 2, n). Вычислить значения частичных сумм ряда Фурье для n = 10, 20, 50 в точках x= -p, 0, p / 2, p. Функция f (x)имеет следующий вид:
Указания: 1. Открыть панели инструментов, нажав на кнопки 2. Ввести функцию f(x). 3. Нажать кнопку: = на калькуляторе. 4. В панели программирования щелкнуть по кнопке Add Line. Появляется вертикальная черта с двумя строками ввода.
5. Перейти в первую строку. Щелкнутьо кнопке if. Появляется оператор if. В левое поле ввода записываем выражение для вычисления функции, справа ограничения на аргумент. 6. При вводе выражений использовать панели калькулятора, знаков отношений и греческого алфавита.
8. Ввести a, нажать < [ > (знак нижнего индекса) и k - получим ak. Ввести: = и выражение для ak. 9. Аналогично ввести bk. 10. Ввести выражение для вычисления сумм ряда Фурье S (x, n). 11. Задать таблицу значений аргумента x на отрезке [-p, p] с шагом p / 100: x: = -p, -p + p / 100.. p. 12. Ввести имя частичной суммы, указав в скобках нужные значения аргументов, и нажать < = >. На экране отобразятся значения функции в точках. Задание. Вычислить производную 1-го порядка для функции f (x). Построить графики производных функции f (x). Указания: 1. Все операции выполнять так же как в предыдущих заданиях. 2. Для ввода символа производной открываем панель
f?(x): = Строим график функции f (x) для значений аргумента Задание. Выполнить аналитическое вычисление коэффициентов Фурье. Указания: 1. Для получения аналитических выражений коэффициентов Фурье копируем в рабочий документ формулы для вычисления и выделяем их. 2. Открываем панель Ключевые слова символьных вычислений нажимаем кнопку Преобразовать 3. В результате ввода получаем на экране следующие выражения:
4. Используя полученные аналитические выражения для коэффициентов Фурье, выполнить их вычисление. 5. Сравнить результаты вычислений с ранее полученными. 6. Подготовить отчет в виде экранных форм. Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
ПРОИЗВОДНАЯ И ЕЕ ВЫЧИСЛЕНИЕ Пусть функция f(x) определена на промежутке (а, b), точка
Здесь f ( Порядок выполнения работы 1). Найдите по определению производную функции f (x)= Вычислите значение производной в точке x = 0. Поскольку f (0) = 0, то приращение функции Указание: 1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали. 2. Определите функцию. 3. Определите приращение функции в указанной точке. 4.Вычислите предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю. 5. Вычислите производную аналитически. Фрагмент рабочего документа Mathcad, содержащего необходимые вычисления, приведен ниже.
Значение функции при x, отличном от нуля
Производная функции f (x) в точке х =0 существует и равна 4. f (x)=4
Рис. 35. Символьное дифференцирование Указание. Символ приращения
Рис. 36. Дифференцирование с использованием панели Calculus
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа. Индивидуальные задания к лабораторной работе 8. Найдите производную функции f(x). Вычислите значение производной в точке x=0, имея в виду, что f(0)=0.
* Возможно (а, b) = (-бесконечность,+бесконечность). Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение?
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1000; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |


 где ak и bk - коэффициенты Фурье, которые вычисляют по формулам Эйлера - Фурье:
где ak и bk - коэффициенты Фурье, которые вычисляют по формулам Эйлера - Фурье:


 ,
,  ,
,  ,
,  .
.
 7. Ввести n:= 50 и k:= 0 .. n.
7. Ввести n:= 50 и k:= 0 .. n. и нажимаем кнопку
и нажимаем кнопку  .
. 3. В результате ввода получаем на экране выражение для функции f (x) в следующем виде:
3. В результате ввода получаем на экране выражение для функции f (x) в следующем виде:

 и щелкаем по рабочему документу правее и ниже стрелки.
и щелкаем по рабочему документу правее и ниже стрелки.


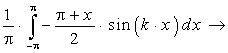





 Лабораторная работа 13
Лабораторная работа 13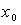 произвольная точка из области определения функции*. Обозначим через
произвольная точка из области определения функции*. Обозначим через  -> f (
-> f (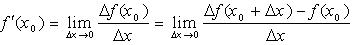 .
. .
.
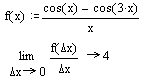







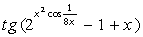

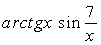


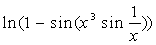
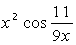


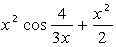



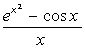

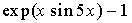
 Литература:
Литература: Лабораторная работа 14
Лабораторная работа 14


