Покажите работу преподавателю.

Содержание отчета

1. Титульный лист.

2. Решение всех задач с комментариями.

Контрольные вопросы

19. Перечислите основные возможности символьной математики.

20. Каким образом можно задать упрощение выражения?

21. Каким образом можно получить значение числа π с точностью 25 знаков после запятой?

22. Каким образом можно выполнить разложение по степеням переменной?

23. Каким образом можно найти неопределеный интеграл от выражения?

24. Каким образом можно решить уравнение?

Литература:

16. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.

17. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил.

18. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.

19. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с.

20. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.

Лабораторная работа №17

Расчёты с помощью математической системы MathCAD.

Цель работы: применение некоторых символьных выражений.

Основные положения по л.р. №4.

I. Рабочий файл и другие документы сохраняйте в своём рабочем каталоге

II. Отчёт по лабораторной работе представляет собой документ MathCAD, с выполненными заданиями. При заполнении отчёта необходимо указать номер задания, кратко — тему, а затем вписать ответ.

Создайте новый документ MathCAD и выполните следующие задания:

Задание 1. Построение графиков в полярной системе координат.

Постройте график sin(2·x)², изменение х возьмите за полный период с шагом 0,01.

Пример:

Пределы, для построения графика

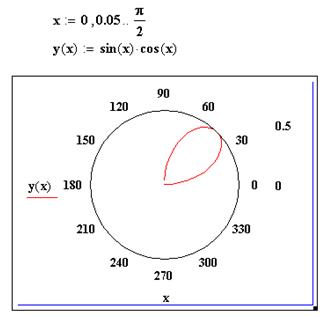
Задание 2. Использование функций с условиями сравнения. Используйте функцию if(условие,выражение1(если условие истинно),выражение2(если условие ложно)), для построения графиков sin(x) и cos(x) в декартовой системе координат. В качестве условия вывода графика для sin(x) — только положительные значения, для cos(x) — только отрицательные значения.

Пример: f(x):=x² y(x):=if(f(x)≥ 2,f(x),0)

Задание 3. Работа с векторами и матрицами.

Задайте вектор V1 размерностью [5,1] (<CTRL>+M) со следующими значениями: (0,5 5 –4 2 1,9). Затем задайте вектор с такой же размерностью V2 (8 -4 2 0 -5,8). Произведите следующие операции, не изменяя начальных данных, а просто выводя результат:

 

• Умножьте вектор V1 на 3
• Сложите V1 c V2
• Умножьте V1 на V2 скалярно
• Умножьте V1 на V2 векторно
• Вычислите сумму элементов обоих векторов.

· Объедините два вектора V1 и V2 в одну матрицу с именем M1 и выведите значения её элементов (должна получиться матрица размерностью 2 на 5).

· Создайте матрицы в качестве элементов главной диагонали которых будут элементы векторов V1 и V2.

· Создайте матрицу, элементами которой будут значения любой придуманной вами функции двух аргументов. Затем выведите произвольную подматрицу, полученной вами матрицы.

· Создайте единичную матрицу произвольного порядка

· Объедините два вектора V1 и V2 в единый вектор V3

Функции определения матриц и операции с блоками матриц:

matrix(m, n, f) - создает и заполняет матрицу размерности m*n, элемент которой, расположенный в i-ой строке, j - ом столбце, равен значению f(i,j) функции f(x,y);

 

diag(v) - создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;

 

identity(n) - создает единичную матрицу порядка n;

 

augment(A,B) - формирует матрицу, в первых столбцах которой содержится матрица A, а в последних матрица B (матрица A и B должны иметь одинаковое число строк);

 

stack(A,B) - формирует матрицу, в первых строках которой содержится матрица A, а в последних матрица B (матрица A и B должны иметь одинаковое число столбцов);

 

submatrix(A, ir, jr, ic, jc) - формирует матрицу, которая является блоком матрицы A, расположенной в строках с ir по jr и в столбцах c ic по jc, ir<=jr, ic<=jc

Задание 4. Решение системы уравнений.

Решите уже знакомую вам по лабораторным работам по EXEL систему уравнений 2 –мя способами. (Используя обратную матрицу и используя блок численного решения уравнений GIVEN FIND).

 

Варианты для выполнения задания №4

Задания определены общей для всех вариантов матрицей A и различными векторами B, показанными в таблице.

Матрица A

Вектор B

№	b1	b2	b3	b4	b5	b6		№	b1	b2	b3	b4	b5	b6
	-21				-11							-49	-43	-48
					-55				-13			-54		-84
	-46				-18	-8			-40			-89	-28	-90
	-27				-10	-4			-92			-51	-47	-78
	-29				-9	-10			-33			-64	-91	-48
	-28			-9	-21	-18						-87	-73	-60
				-29	-27	-16			-84			-32	-45	-82
				-35	-29	-18			-65			-24	-69	-60
				-28	-37	-14			-92			-24	-59	-80
			-7	-21	-44	-8			-96			-26	-62	-84
	-35			-55	-44	-50			-76			-26	-99	-50
	-46			-91	-22	-80			-93			-21	-99	-54
				-48	-48	-28			-90			-16	-99	-64
			-1	-65	-43	-34			-79			-27	-99	-68
				-16	-57	-24			-76			-22	-99	-68