
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функций на экстремум и поиск корней уравнений.Содержание книги
Похожие статьи вашей тематики
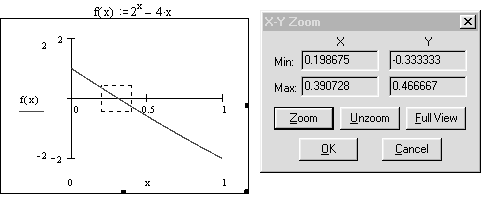
Поиск на нашем сайте Задание: Найти наибольшее и наименьшее значения функции f(x) = 2х 4x на отрезке [0, 1]; решить на этом отрезке уравнение 2х 4х = 0. Порядок выполнения: 1. Установите автоматический режим вычислений и режим ото-бражения результатов символьных вычислений по горизон-тали. 2. Определите выражение для функции. 3. Постройте график функции. 4. Найдите наибольшее и наименьшее значения функции на отрезке. 5. Решите уравнение f(x) =0, используя функцию root, выбрав в качестве нулевого приближения сначала левую, а потом правую границу заданного отрезка. Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями и графиком.
Указание. Функция, рассмотренная в примере, непрерывна на отрезке и монотонно убывает на нем. Наибольшего значения функция достигает в левом конце отрезка, в точке х = 0, наименьшего в правом конце, в точке х = 1. Для вычисления нуля функции на отрезке используйте встроенную функцию root(f, х). Перед обращением к root(f, х) необходимо присвоить переменной х начальное значение. В приведенном фрагменте корень вычислялся дважды, в качестве начального прибли-жения использованы сначала левый, а потом правый конец отрезка. Для того чтобы найти корень уравнения графически, используйте операцию вычисления координат точки на кривой. Более точные значения координат корня можно получить, увели-чив график в окрестности корня, с помощью операции Zoom пункта Graph меню Format.
Ниже представлены фрагменты рабочего документа Mathcad, в которых приведены результаты соответствующих операций и график функции на промежутке (0;6).
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Найдите (аналитически и графически) точки, в которых достигаются наибольшее и наименьшее значения заданной на отрезке не-прерывной функции. Найдите нуль функции на заданном отрезке. (Решите уравнение f(x) =0.)
1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Какие корни позволяет определить метод хорд? 2. В чем заключается геометрический смысл метода хорд? 3. Всегда ли метод хорд позволяет вычислить отделенный корень с заданной погрешностью? 4. Как выбираются концы отрезка интервала в методе хорд? 5. Какими свойствами должна обладать функция f(x) для того, чтобы методом хорд можно решить уравнение f(x)=0? 6. Какой конец хорды неподвижен при реализации метода? В чем заключается геометрическая интерпретация метода Ньютона? 8. Исходя из чего выбирается в методе Ньютона первое приближение x0? 9. Как выбираются концы «закреплённого» отрезка интервала в методе Ньютона при 10. Как выбираются концы «закрепленного» отрезка интервала в методе Ньютона при 11. Что необходимо для того, чтобы уравнение f(x)=0 решалось методом Ньютона? 12. В каких случаях применение метода Ньютона не рекомендуется? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с. ЛАБОРАТОРНАЯ РАБОТА № 7
Цель работы: С помощью средств MathCAD научиться находить графическое, аналитическое, численное решения уравнений. Исследовать на разрешимость системы уравнений. Рекомендуемая литература: [1–5, 10]. Задание: 1. Найти все корни уравнения n -й степени: графически, численно и аналитически. 2. Сделать проверку полученного решения. 3. Найти численное и графическое решение трансцендентного уравнения. 4. Сделать проверку полученного решения. 5. Исследовать систему уравнений на разрешимость. Построить график. 6. Решить систему уравнений. 7. Сделать проверку полученного решения. Пример выполнения задания: Задание:
1. Найдем решение кубического уравнения. Для этого запишем его коэффициенты в следующем виде:
Определим полином
Найдем решение уравнения y(x)= 0 графически. Для этого построим график, как это было описано в лабораторной работе № 2, но не указывая границы по оси Y (эти границы MathCAD проставляет сам). В результате получаем:
Мы видим, что корни лежат в интервалах [-2; -1], [1; 2], [3; 4]. Получим корни уравнения y(x)= 0 аналитически. Для этого в MathCAD предназначена функция solve на панели инструментов «Символы». Имеем:
Можно убедиться, что наша оценка корней по графику была верной. Для нахождения корней уравнений n -й степени имеется специальная функция polyroots, в качестве параметра которой задается вектор коэффициентов:
В MathCAD имеется функция root, которая позволяет находить корень из заданного интервала для любых уравнений. В частности, для уравнений n -й степени имеется два способа использования этой функции. Примечание. В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня. Первый способ. Задаем начальное значение x:
Вызываем функцию:
где y(x) – заданная левая часть уравнения y(x)= 0; x – приближенное значение аргумента; (–2) – левый край интервала, которому принадлежит искомый корень; (–1) – правый край интервала. Для просмотра полученного значения достаточно набрать «X11=», получим:
Оставшиеся два корня ищутся аналогично:
В результате получим:
Второй способ. Задаем начальное значение x: = -1
Здесь интервалы не указываем, и функция ищет ближайший к заданному значению корень:
Для нахождения второго корня задаем значение x: = 1
Получили значение:
Третий корень ищем по аналогии:
2. Выполним проверку полученного решения:
Мы видим, что корень из интервала [1; 2] более точно найден функцией solve. 3. Трансцендентные уравнения можно решать графически, разбив уравнения на два более простых. Например, наше уравнение, заданное в виде
разобьем на два:
Построим графики этих уравнений:
4. Выполним проверку полученного решения:
Можно увидеть, что корни находятся с достаточно хорошей точностью, но с удалением от точки 0 точность начинает ухудшаться. 5. Зададим систему уравнений матрицей А и вектором правых частей f:
Проведем исследование данной системы на разрешимость, для этого вычислим определитель матрицы А:
Определитель матрицы не равен нулю, следовательно, наша система разрешима и имеет единственное решение. Получим данное решение графически. Для этого построим каждую плоскость отдельно. В MathCAD плоскости задаются так:
Графическое представление этих плоскостей имеет вид:
В пересечении мы получим одну общую точку для всех плоскостей, которая и будет решением данной системы. 6. Решим систему уравнений матричным методом. Для этого найдем обратную матрицу:
Вектор неизвестных имеет вид:
7. Сделаем проверку:
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
«Метод наименьших квадратов. Регрессия» Цель работы: Познакомить читателя с основами обработки экспериментальных данных с помощью фундаментальных численных методов и встроенных функций системы MathCAD. Рекомендуемая литература: [1–3, 7, 10]. Задание: 1. По заданной выборке построить аппроксимацию на основе заданного набора базисных функций с помощью метода наименьших квадратов. 2. На основе набора базисных функций, предложенного в п. 1, построить регрессию для заданной выборки. 3. Провести сравнение результатов п. 1 и п. 2. Пример выполнения задания: Задание:
Базис произвольных функций: cos(x), x2, ex, ln(x+1), sin(x). 1. Для удобства работы рекомендуем отсортировать выборки так, как это делалось в лабораторной работе № 2. Получим:
Зададим константы: N – номер последнего элемента выборки, n – число базисных функций минус единица и параметр i:
Далее зададим набор функций:
Примечание. Обращаем ваше внимание на то, что если записано f0(x1), то и функция, записанная Вычислим значения заданных функций в точках выборки x:
Сформируем матрицу системы уравнений для нахождения коэффициентов пробной функции. Для этого зададим параметры:
Формируем матрицу по формуле:
Далее строим вектор правых частей для данной системы уравнений:
Решаем нашу систему уравнений M*a=f (см. лабораторную работу № 3). После чего получаем требуемую аппроксимацию:
График аппроксимации P(X) и экспериментальные точки представлены на рисунке:
2. Функцию аппроксимации можно построить с помощью встроенных возможностей MathCAD. Но если все выше указанные вычисления мы можем проводить для не отсортированной выборки, то встроенные функции MathCAD требуют, чтобы выборка была отсортирована по x. После того как выборка отсортирована, можно построить вектор базисных функций:
Далее ищем коэффициенты пробной функции с помощью встроенной функции пользователя linfit:
где x, y – элементы выборки; F – вектор базисных функций. Теперь можно построить аппроксимацию g:
Для графического представления g(z) необходимо задать интервал изменения переменной z и шаг Dz:
В результате получим, что график имеет вид:
3. Сравним полученные результаты. Для этого вычислим относительную разницу между аппроксимациями полученными в п. 1 и 2:
На первом графике представлены точки выборки и кривые аппроксимации из п. 1 и 2, а на втором – относительная разница f(x):
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Перечислите основные возможности символьной математики. 2. Каким образом можно задать упрощение выражения? 3. Каким образом можно получить значение числа π с точностью 25 знаков после запятой? 4. Каким образом можно выполнить разложение по степеням переменной? 5. Каким образом можно найти неопределеный интеграл от выражения? 6. Каким образом можно решить уравнение? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
«Программирование в MathCAD. Линейное программирование.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |






 Индивидуальные задания к лабораторной работе 6.
Индивидуальные задания к лабораторной работе 6.
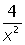
 -16
-16
 -1
-1
 -x-0.5
-x-0.5












 Содержание отчета
Содержание отчета <0 на концах интервала?
<0 на концах интервала? «Решение уравнений и систем»
«Решение уравнений и систем»





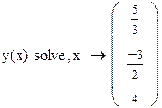



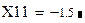
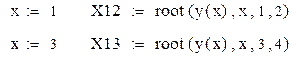



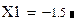








 По графику видно, что все корни уравнения лежат в интервале (-¥;0). Найдем несколько корней при помощи функции root (интервалы можно подобрать по графику):
По графику видно, что все корни уравнения лежат в интервале (-¥;0). Найдем несколько корней при помощи функции root (интервалы можно подобрать по графику):


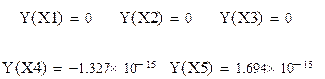





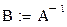 .
. Теперь можно найти решение системы:
Теперь можно найти решение системы:  .
.


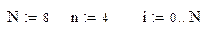
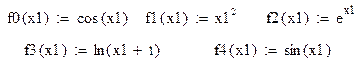
 справа от знака «присвоить», – тоже от x1(cos(x1)), а не от x.
справа от знака «присвоить», – тоже от x1(cos(x1)), а не от x.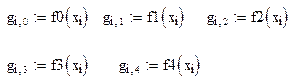



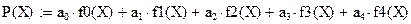




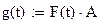
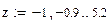





 ЛАБОРАТОРНАЯ РАБОТА № 9
ЛАБОРАТОРНАЯ РАБОТА № 9


