
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции и построения её графикаСодержание книги
Поиск на нашем сайте После того как мы обсудили многие аспекты поведения функции и способы их исследования, сформулируем общую схему исследования функции. Эта схема даст нам практический способ построения графика функции, отражающего основные черты её поведения. Пусть дана функция 1). Найти её область определения 2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси 3). Выяснить, как ведёт себя функция при приближении аргумента Пример 7.36 Пусть 4). Если область определения 5). Найти точку пересечения графика с осью 6). Найти интервалы монотонности функции На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках. 7). Найти интервалы выпуклости и вогнутости функции. Это делается с помощью исследования знака второй производной 8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой. После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график. 41. Определение функции нескольких переменных. Геометрическое изображение функции двух переменных. Частное и полное приращение функции. Граница и непрерывность функции. Частные производные функций нескольких переменных. Полное приращение и полный дифференциал. Если каждой паре 2-х независимых переменных (х;у) є Д из области Д можно поставить во взаимное однозначное соответствие некоторого значения z, то z называется функцией 2-х переменных. Z=f(x;y) Геометрическое изображение функции 2-хпеременных: Задана функция z=f(x;y) и область определения функции (х;у) є Д тогда геометрическое изображение Z называется совокупностью точек Р(х;у), координаты которых удовлетворяют исходному z=f(x;y). Геометрическим аналогом функции 2-х переменных есть некоторая поверхность в пространстве проэктирующаяся на плоскости ОХУ в области определения Д. Частное преращение функции: Пусть задана функция z=f(x;y), предложим, что у=константа, а х получило преращение в Δх, тогда рассмотрим соответственное преращение функции F(x+Δx,y)-f(x,y)= ΔxZ это называется частным преращением функции по переменной х. Аналогично получаем частное преращение по переменной у. Полное преращение функции: Δz=f(x+Δx,y+Δy)-f(x,y) при чем Δz не равна ΔxZ+ΔyZ Аналогично находим частное и частное преращение для функции числа переменных. Непрерывность функции: Пусть т.М0(х0,у0) є Д функции z=f(x,y) тогда функция z=f(x,y) является неприрывной в т.М0, если выполняется равенство lim f(x,y)=f(x0,y0) где х и у стремятся к х0 и у0 – в этом случае функция называется непрерывной в т. М0(х0,у0) Существует и 2-ое определение непрерывности: LimΔz=0 Δx и Δу стремятся к 0 Функция непрерывна в каждой точке области, является непрерывной во всей области. Частные производные функций нескольких переменных: Частные производные функции z=f(x;y) по переменной х, называется придел отношения частного преращения по переменной х по Δх, тогда Δх стремится к 0. Lim ΔxZ/Δх=dz/dx при Δх стремится к 0 Аналогично дается определение по переменной у Lim ΔуZ/Δу=dz/dу при Δу стремится к 0 При нахождение частной производной по переменной х,у=константа, а когда берем частную производную по переменой у то х=константа. Определение Если функция z= f(x,y) дифференцируема в точке Р0(х0, у0), то главная, линейная относительно приращения аргументов, часть ее полного приращения называется полным дифференциалом функции и обозначается dz|p0=df(x0,y0)=f’x(x0,y0) Δx+f’y(x0,y0) Δy.
Дифференцирование сложной функции. Полная производная и полный дифференциал. Производная от функции заданной неявно. Скалярное поле. Производная по направлению и градиент. Касательная и нормальная плоскость к пространственной кривой. Касательная плоскость и нормаль к поверхности. Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке Пусть даны функции, определённые в окрестностях на числовой прямой,
[Замечание В обозначениях Лейбница цепное правило для вычисления производной функции
Определение. Производная от функции z=f(x,у) по х, найденная в предложении, что у остается постоянным, называется частной производной от z по х и обозначается
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 . Для её исследования нужно:
. Для её исследования нужно: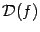 . Если это не слишком сложно, то полезно найти также область значений
. Если это не слишком сложно, то полезно найти также область значений  . (Однако, во многих случаях, вопрос нахождения
. (Однако, во многих случаях, вопрос нахождения 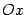 ), не является ли она периодической.
), не является ли она периодической. к граничным точкам области определения
к граничным точкам области определения  Эта функция определена на всей числовой оси, однако 0 является точкой разрыва функции: при
Эта функция определена на всей числовой оси, однако 0 является точкой разрыва функции: при  функция стремится к
функция стремится к  . Значит, вертикальная прямая
. Значит, вертикальная прямая  служит вертикальной асимптотой функции, хотя функция и определена в точке
служит вертикальной асимптотой функции, хотя функция и определена в точке  или
или  , то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при
, то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при  или
или  соответственно.
соответственно. (если
(если  ). Для этого нужно вычислить значение
). Для этого нужно вычислить значение  . Найти также точки пересечения графика с осью
. Найти также точки пересечения графика с осью  (или убедиться в отсутствии корней). Уравнение
(или убедиться в отсутствии корней). Уравнение  .
.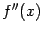 . Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.
. Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. , а функция g имеет производную в точке
, а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке
, то сложная функция h(x) = g(f(x)) также имеет производную в точке  где
где 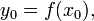 и
и  Пусть также эти функции дифференцируемы:
Пусть также эти функции дифференцируемы:  Тогда их композиция также дифференцируема:
Тогда их композиция также дифференцируема:  и её производная имеет вид:
и её производная имеет вид:
 где
где  принимает следующий вид:
принимает следующий вид:
 или f'x (x, у). Аналогично определяется и обозначается частная производная z по у.
или f'x (x, у). Аналогично определяется и обозначается частная производная z по у. 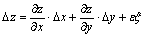 , (1)
, (1) при
при  .
.


