
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственное значение и собственные векторы матрицы.Содержание книги
Поиск на нашем сайте
Пусть задан вектор Х=
Если после преобразования вектора Х с помощью матрицы А получается вектор I= A * X и вектор I = ʎX, то вектор Х называется собственным вектором линейного преобразования матрицы А, а ʎ cобственным значением. Отсюда А*Х= ʎ*Х (1) АХ-ʎ*Х*Е=0 (А-ʎЕ)Х=0 (2) – если расписать в буквенном виде
Если определитель равено 0 то однородная система (3) имеет не нулевое решение
Дельта = Раскрыв определитель «дельта» получаем уравнение 3-го порядка ʎ^3 + b1 ʎ^2 +b3 = 0 (5) – характеристическое уравнение
Решая его найдем корни ʎ1, ʎ2, ʎ3 это будут собственные значения
Собственные вектора – для этого подставляем корни ʎ1, ʎ2, ʎ3
ʎ1: ʎ2: ʎ3:
6. Определение вектора. Модуль вектора. Определение компланарных, коллинеарных и равных векторов.
Вектором называется направленный отрезок (модулем) вектора Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны. Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:
Проекция вектора на ось. Разложение вектора на ось по единичным векторам. Проекцией вектора Проекция вектора Проекции равных векторов на одну и туже ось равны. Вектор
Проекция вектора
Проекция вектора
Система ортов (или базисная система векторов) - это система единичных векторов осей координат. Орт координатной оси
Для любого вектора Если вектор Умножение вектора на число. Сложение и вычитание вектора. Произведение ненулевого вектора на число - это вектор, коллинеарный данному, а его модуль равен модулю данного вектора, умноженному на модуль числа. Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число. Так в случае плоской задачи произведение вектор на a = {ax; ay} на число b находится по формуле a ·b = {ax · b;ay · b}
b находится по формуле a ·b = {ax · b;ay · b;az · b}
При сложении двух векторов
Проекции результирующего вектора на координатные оси при сложении векторов равны алгебраической сумме проекций слагаемых векторов
При вычитании векторов проекции результирующего вектора равны разности проекций векторов
Расстояние между двумя точками в прямоугольной системе координат. Деление отрезка в данном отношении. Расстояние d между двумя точками M1(x1,y1,z1) и M2 (x2,y2,z2) в пространстве определяется формулой
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |

 такой что х1(кв)+х2(кв)+х3(кв)
такой что х1(кв)+х2(кв)+х3(кв) 
 (3)
(3)



 ; точка
; точка 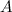 - начало, точка
- начало, точка  - конец вектора. Характеризуется величиной ии направлением.
- конец вектора. Характеризуется величиной ии направлением.
 , если
, если 
 называется длина отрезка
называется длина отрезка  , взятая со знаком "+", если направление
, взятая со знаком "+", если направление  совпадает с направлением вектора
совпадает с направлением вектора  , и со знаком "-", если направление
, и со знаком "-", если направление  .
.
 на некоторую ось
на некоторую ось 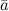 , умноженного на число
, умноженного на число  :
:

 обозначается через
обозначается через  , оси
, оси  - через
- через  , оси
, оси  - через
- через  (рис. 1).
(рис. 1).
 , который лежит в плоскости
, который лежит в плоскости  , имеет место следующее разложение:
, имеет место следующее разложение: 
 расположен в пространстве, то разложение по ортам координатных осей имеет вид:
расположен в пространстве, то разложение по ортам координатных осей имеет вид: 
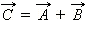 суммарный вектор
суммарный вектор  представляет собой диагональ параллелограмма, построенного на векторах
представляет собой диагональ параллелограмма, построенного на векторах  и
и  как на сторонах (начала всех трех векторов должны совпадать). По этому же правилу производится операция вычитания векторов
как на сторонах (начала всех трех векторов должны совпадать). По этому же правилу производится операция вычитания векторов



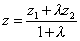

 Координаты x, y, z точки М, которая делит отрезок MM1, ограниченный точками M1(x1,y1,z1) и M2 (x2,y2,z2), в отношении
Координаты x, y, z точки М, которая делит отрезок MM1, ограниченный точками M1(x1,y1,z1) и M2 (x2,y2,z2), в отношении  ,определяется по формулам:
,определяется по формулам:
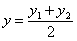
 В частности,
В частности,  при имеет координаты середины данного отрезка:
при имеет координаты середины данного отрезка:


