
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипербола. Определение. Вывод канонического уравнения.Содержание книги
Поиск на нашем сайте
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная. Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF1 – MF2|=2a или MF1 – MF2=±2a,
25.переменные и постоянные величины множества. Функции. Область определения, способы задания. График функции. Приращение функции. Переменная величина – такая величина, которая может принимать любые значения X Y Z. Постоянная величина – константа, которая сохраняет всегда одно и тоже значение. Функции – если каждому значению переменной Х соответствует одно и только одно значение переменной У, то У является функцией от Х, у=f(x). Область определения функции D(f) – называется множество значений Х при которых функция существует. Способы задания: 1) табличный; 2)графический; 3)аналитический. График функции – это множество точек, у которых абсциссы являются допустимыми значения аргумента Х, а ординаты – соответствующими значениями функции У. Приращения функции – это свойство функции f(x) быть не прерывной в точке, то есть это разность между двумя значениями функции. Если есть 2 точки Х и А на числовой оси, то на отрезке(х;а) функция должна существовать и если существует разность f(x)-f(a) где х бесконечно много приближается по своему значению к значению а(этот отрезок очень маленький), то это и есть приращение функции. f(x)-f(a) – приращение функции. Предел переменной величины (последовательности). Предел функции при непрерывном стремлении аргументы к конечному значению или к бесконечности. Свойства функций, имеющих предел. Придел переменной величины – это постоянное число а является приделом переменной величины х, если для любого + эпсилент>0найдется такое значение переменной х с которого будет выполнятся неравенство lim x=a, |x-a|<E
Придел функции – пусть функция y=f(x)определена в некоторой окрестности т.А, х=а, тогда число В является приделом функции при х стремится к А если для любого + эпсилент существует дельта зависящая от эпсилент>0, такое что как только |x-a|<дельта, то выполняется условие |f(x)-b|<E
Придел функции слева: если f(x) стремится к приделу В1, так что х принимает значение<A, то limf(x)=B1 X стремится к а-дельта Придел функции справа: если f(x) стремится к приделу В2, так что х принимает значение>A, то limf(x)=B2 X стремится к а+дельта Бесконечно малые и бесконечно большие величины и их свойства.Сравнение бесконечно малых,эквивалентность бесконечно малых.Их использование для отыскания пределов и приближенных вычислениях.Неопределённые выражения. Бесконечно малые величины: функция А=А(х) бесконечно малой если limA(x)=0 Х стремится к а Свойства бесконечно малых: Теорема 1: если функция у=в+А, где А-бесконечно малая функция, а в=константе, то lime=в. Теорема 2: если А(х) стремится к 0, то обратная ее функция к бесконечности 1/А(х)стремится к бесконечности. Теорема 3:елгебраическая сумма конечного числа бесконечно малой функции есть величина бесконечно малой. Теорема 4: произведение бесконечно малой на ограниченную функцию есть функция бесконечно малая. Теорема 5:частное отделение бесконечно малой на функцию lim не равен 0, есть величина бесконечно малая. Бесконечно большие величины: функция является бесконечно большой если Limf(x)= бесконечности X стремится к а Основные свойства бесконечно больших: Теорема 1:если Limf(x)= в, где в – конечное число, то функция f(x) ограниченая X стремится к а Теорема 2: если Limf(x)= в не ровна 0, то функция 1/f(x) – величина ограниченая. X стремится к а Теоремы о пределах суммы, произведения и частного, признаки существования предела: А) для монотонной ограниченной последовательности; Б) для функции, заключенной между двумя функциями. Основные теоремы о приделах: Теорема 1: придел алгебраической суммы конечного числа переменных или функции = сумме приделов или переменных этих функций. Теорема 2: придел произведения переменных или функции = произведению приделов. Следствие: постоянный множитель С можно выносить за знак придела. Lim C U=C lim U Теорема 3:придел дроби = дроби придела, если знаменатель не равен 0. Теорема 4: если между соответствующими значениями функции существует неравенство U(x)<=Z(x)<=V(x) и lim u(x)=lim v(x)=b x стремится к a x стремится к a2,
то lim z(x)=b x стремится к а Теорема 5:если для функции выполняется неравенство U(x)>=V(x) и limU(x)=b1, limV(x)=b2 при х стремится к а, то b1>=b2 Теорема 6: если V(x)>=0 и limU(x)=b при а стремится к 0, то b>=0 Теорема 7: если переменная величина V возрастает и ограниченный сверху V<=M и имеет limV=b, то b<=M. Аналогично формулируется теорема при ограничении снизу, если переменная величина b спадает и ограничена снизу m<=V, limV(x)=b1, то m<=b1.
29.Первый замечательный предел. 1 замечательный предел.
Возьмем круг радиуса 1, обозначим радианную меру угла MOB через Х. Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда
Разделим все на
Т.к. Следствия · · · ·
Примеры. 1. 2.
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.20.252 (0.007 с.) |



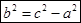
 Так как числовая последовательность является частным случаем переменной, то ее придел определяется как число а является приделом при n стримящимся к бесконечности. {xn}, n бесконечность.
Так как числовая последовательность является частным случаем переменной, то ее придел определяется как число а является приделом при n стримящимся к бесконечности. {xn}, n бесконечность.


 и получим:
и получим: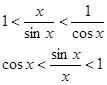
 , то по признаку существования пределов следует
, то по признаку существования пределов следует  .
.



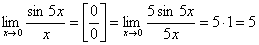 .
. .
.


