
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремумы функции. Необходимый признак экстремума. Достаточный признак экстремума, использующие первую и вторую производную.Содержание книги
Поиск на нашем сайте
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)). Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) > 0 (f ' (x) < 0). Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)). Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами. Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет. Второе достаточное условие. Пусть функция f(x) имеет производную На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Исследование условий и построение графиков. - найти область определения функции - найти точки пересечения графика с осями координат - найти интервалы знака постоянства - исследовать на четность, нечетность - найти асимптоты графика функции - найти интервалы монотонности функции - найти экстремумы функции - найти интервалы выпуклости и точки перегиба Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры. Вертикальная Вертикальная асимптота — прямая вида Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например: 1. 2. Замечание: обратите внимание на знаки бесконечностей в этих равенствах. [править]Горизонтальная Горизонтальная асимптота — прямая вида
[править]Наклонная Наклонная асимптота — прямая вида
Пример наклонной асимптоты 1. 2. Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот! Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен Связь между наклонной и горизонтальной асимптотами Если при вычислении предела Дело в том, что горизонтальная асимптота является частным случаем наклонной при 1. Функция имеет или только одну наклонную асимптоту, или одну вертикальную асимптоту, или одну наклонную и одну вертикальную, или две наклонных, или две вертикальных, либо же вовсе не имеет асимптот. 2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.
График функции с двумя горизонтальными асимптотами ]Нахождение асимптот Порядок нахождения асимптот 1. Нахождение вертикальных асимптот. 2. Нахождение двух пределов 3. Нахождение двух пределов если [править]Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например: Дана функция Разделив нацело числитель на знаменатель, получим:
При
и [править]Свойства · Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости[4]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 632; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.006 с.) |

 в самой точке xо. Если f ' (xо) = 0,
в самой точке xо. Если f ' (xо) = 0,  при условии существования предела
при условии существования предела  .
.

 при условии существования предела
при условии существования предела .
. при условии существования пределов
при условии существования пределов



 ), то наклонной асимптоты при
), то наклонной асимптоты при  (или
(или 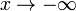 ) не существует!
) не существует!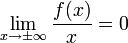 , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
, то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?
 в п. 2.), то
в п. 2.), то  , и предел
, и предел 
 .
. .
. ,
,  , то есть:
, то есть: ,
, является искомым уравнением асимптоты.
является искомым уравнением асимптоты.


