
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратные матрицы и их свойства. Определители и их свойства, вычесление определителей второго и третьего порядка. Минор и алгебраическое дополнение.Содержание книги
Поиск на нашем сайте
Квадратные матрицы и их свойства. Определители и их свойства, вычесление определителей второго и третьего порядка. Минор и алгебраическое дополнение.
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Общие свойства:1)Общий множитель элемента одного столбца можно вынести за знак определителя;2)Велечина определителя не изменится,если к элементу1 столбца прибавить элементы 2 столбца умножив на произвольное одинаковое число. Определители и их свойства 1. 2. 3.
Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали. Свойства: 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. 2. При перестановке двух параллельных рядов определитель меняет знак. 3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю. 4. Общий множитель элементов можно вынести за знак определителя. 5. Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей. 6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число. 7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение. Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю. Определитель второго порядка вычисляется по формуле:
Определитель третьего порядка вычисляется по формуле:
Минор Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s. Алгебраическим дополнением элемента
где
Системы линейных алгебраических уравнений. Правило Крамера. Метод Гаусса. Системы линейных алгебраических уравнений -это система уравнений вида
Правило Крамера Если в системе Метод Гаусса Определение. Две системы линейных уравнений называются равносильными, если множество всех их решений совпадает. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. 3.Матрицы любого порядка. Общие понятия. Виды матриц.Действия над матрицами(умножение на число, сложение и умножение матриц). Обратная матрица. Ранг матриц. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. Матрица, у которой всего одна строка Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей. Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.
где 1. 2. 3. 4. Матрица, полученная заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной, к данной.
1.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Обратная матрица. Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратная матрица матрице А, обозначается через А1, так что В = А1 и вычисляется по формуле, где А i j - алгебраические дополнения элементов a i j матрицы A.
Рангом матрицы Теорема Кронека-Капелли Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когдаранг матрицысистемы равен рангу расширенной матрицы. RgA = RgA* Решение системы линейных алгебраических уравнений по матричному методу определяется равенством
Нормальное уравнение прямой
где p - длина перпендикуляра (нормали), опущенного из начала координат на прямую, а Угол между прямыми. Дано: прямые L1 и L2 с угловыми коэффициентами
Требуется найти угол между прямыми:
Бесконечно малые и бесконечно большие величины и их свойства.Сравнение бесконечно малых,эквивалентность бесконечно малых.Их использование для отыскания пределов и приближенных вычислениях.Неопределённые выражения. Бесконечно малые величины: функция А=А(х) бесконечно малой если limA(x)=0 Х стремится к а Свойства бесконечно малых: Теорема 1: если функция у=в+А, где А-бесконечно малая функция, а в=константе, то lime=в. Теорема 2: если А(х) стремится к 0, то обратная ее функция к бесконечности 1/А(х)стремится к бесконечности. Теорема 3:елгебраическая сумма конечного числа бесконечно малой функции есть величина бесконечно малой. Теорема 4: произведение бесконечно малой на ограниченную функцию есть функция бесконечно малая. Теорема 5:частное отделение бесконечно малой на функцию lim не равен 0, есть величина бесконечно малая. Бесконечно большие величины: функция является бесконечно большой если Limf(x)= бесконечности X стремится к а Основные свойства бесконечно больших: Теорема 1:если Limf(x)= в, где в – конечное число, то функция f(x) ограниченая X стремится к а Теорема 2: если Limf(x)= в не ровна 0, то функция 1/f(x) – величина ограниченая. X стремится к а Теоремы о пределах суммы, произведения и частного, признаки существования предела: А) для монотонной ограниченной последовательности; Б) для функции, заключенной между двумя функциями.
Основные теоремы о приделах: Теорема 1: придел алгебраической суммы конечного числа переменных или функции = сумме приделов или переменных этих функций. Теорема 2: придел произведения переменных или функции = произведению приделов. Следствие: постоянный множитель С можно выносить за знак придела. Lim C U=C lim U Теорема 3:придел дроби = дроби придела, если знаменатель не равен 0. Теорема 4: если между соответствующими значениями функции существует неравенство U(x)<=Z(x)<=V(x) и lim u(x)=lim v(x)=b x стремится к a x стремится к a2, то lim z(x)=b x стремится к а Теорема 5:если для функции выполняется неравенство U(x)>=V(x) и limU(x)=b1, limV(x)=b2 при х стремится к а, то b1>=b2 Теорема 6: если V(x)>=0 и limU(x)=b при а стремится к 0, то b>=0 Теорема 7: если переменная величина V возрастает и ограниченный сверху V<=M и имеет limV=b, то b<=M. Аналогично формулируется теорема при ограничении снизу, если переменная величина b спадает и ограничена снизу m<=V, limV(x)=b1, то m<=b1.
29.Первый замечательный предел. 1 замечательный предел.
Возьмем круг радиуса 1, обозначим радианную меру угла MOB через Х. Пусть 0 < X < π/2. На рисунке |АМ| = sin x, дуга МВ численно равна центральному углу Х, |BC| = tg x. Тогда
Разделим все на
Т.к. Следствия · · · ·
Примеры. 1. 2.
Следствия 1. 2. 3. 4. 5. 6.
Примеры. 1. 2. Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.
Непрерывность функции в точке. Непрерывность суммы, произведения, частного. Односторонние пределы. Односторонняя непрерывность. Точки разрыва функции их классификация. Непрерывность элементарных функций. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего, наименьшего значений, существование промежуточных значений. Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке:
Это означает: - функция определена в точке х0 и в ее окрестности; - функция имеет предел при х→х0 - предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство. Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
Точки разрыва функции – это точки в которых нарушается непрерывность функции. Точка разрыва х0 называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы) 13. При этом, если: - А1=А2 то точка х0 называется точкой устранимого разрыва; - А1≠А2 то точка х0 называется точкой конечного разрыва. |A1 – A2| называется скачком функции. Точка разрыва х0 называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности. Свойства ch(x± y)=chx · chy ± shx · shy, (1) sh(x± y)=shx · chy± chx · shy, (2) ch2x–sh2x=1, (3) ch2x=ch2x+sh2x, (4) sh2x=2shx · chx. (5) 34. Производные основных элементарных функций (степенных, логарифмических, показательных и гиперболических функций). Производная сложной и обратной функции. Производные тригонометрических функций. 1) Производная логарифмической и показательной функции Предполагается, что основание a показательной и логарифмической функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой
Если a = е, то получаем результат в виде
Производная логарифмической функции y = log a x определяется выражением
Для натурального логарифма y = ln x производная равна
2) Производные гиперболических функций
Производные гиперболических функций легко находятся, поскольку гиперболические функции являются комбинациями ex и e−x. Например, гиперболические синус и косинус определяются как
Производные этих функций имеют вид
Остальные формулы доказываются аналогично. 3)Производная степенной функции Если f(x) = xp, где p - действительное число, то
Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то
Производная сложной функции Пусть функция f: [ a, b ] → [ c, d ], а функция g:[ a 1, b 1] → [ c 1, d 1], причём [ a 1, b 1] g ' (f (x 0))· f ' (x 0). Теорема Ролля Пусть функция f: [ a, b ] → R непрерывна на сегменте [ a, b ], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f (a) = f (b). Тогда внутри сегмента [ a, b ] найдется точка ξ такая, что f' (ξ) = 0.
Теорема Лагранжа Если функция f: [ a, b ] → R непрерывна на сегменте [ a, b ] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то
Теорема Коши Если каждая из функций f и g непрерывна на [ a, b ] и имеет конечную или бесконечную производную на ] a, b [ и если, кроме того, производная g' (x) ≠ 0 на ] a, b [, то
3) Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если · Если Правило Лопиталя можно также применять к неопределенностям типа
Правило Лопиталя справедливо также и для односторонних пределов. Теоремы о возрастании и убывании (постоянстве) функций в интервале, достаточный признак. Выпуклость и вогнутость графика функции, точки перегиба. Необходимый признак существования точек перегиба. Достаточный признак существования точки перегиба. Теорема. Если в данном промежутке производная функции положительна, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежутке. Замечание. Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции у-/(х) образует с осью Ох острый угол а (18 а > 0), то функция возрастает в этом промежутке. Если касательная к графику образует с осью Ох тупой угол а (1§ сх < 0), то функция убывает. Достаточный признак возрастания функции. Если f’(х) > 0 в каждой точке интервала I, то функция f возрастает на I. Достаточный признак убывания функции. Если f’(х) < 0 в каждой точке интервала I, то функция f убывает на I. График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба. Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует. Асимптоты графиков функций. Общая схема исследования и построения графиков функции. Примеры. Вертикальная Вертикальная асимптота — прямая вида Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например: 1. 2. Замечание: обратите внимание на знаки бесконечностей в этих равенствах. [править]Горизонтальная Горизонтальная асимптота — прямая вида
[править]Наклонная Наклонная асимптота — прямая вида
Пример наклонной асимптоты 1. 2. Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот! Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен Порядок нахождения асимптот 1. Нахождение вертикальных асимптот. 2. Нахождение двух пределов 3. Нахождение двух пределов если [править]Наклонная асимптота — выделение целой части
Также наклонную асимптоту можно найти, выделив целую часть. Например: Дана функция Разделив нацело числитель на знаменатель, получим:
При
и [править]Свойства · Среди конических сечений асимптоты имеют только гиперболы. Асимптоты гиперболы как конического сечения параллельны образующим конуса, лежащим в плоскости, проходящей через вершину конуса параллельно секущей плоскости[4]. Максимальный угол между асимптотами гиперболы для данного конуса равен углу раствора конуса и достигается при секущей плоскости, параллельной оси конуса.
Дифференцирование сложной функции. Полная производная и полный дифференциал. Производная от функции заданной неявно. Скалярное поле. Производная по направлению и градиент. Касательная и нормальная плоскость к пространственной кривой. Касательная плоскость и нормаль к поверхности. Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке Пусть даны функции, определённые в окрестностях на числовой прямой,
[Замечание В обозначениях Лейбница цепное правило для вычисления производной функции
Определение. Производная от функции z=f(x,у) по х, найденная в предложении, что у остается постоянным, называется частной производной от z по х и обозначается Часные производные и дифференциал высших порядков. Необходимое и достаточное условия существование экстремума функций двух переменных. Наибольшее и наименьшее значение функции. Условные экстремумы. Метод множителей Лагранжа. Квадратные матрицы и их свойства. Определители и их свойства, вычесление определителей второго и третьего порядка. Минор и алгебраическое дополнение.
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Общие свойства:1)Общий множитель элемента одного столбца можно вынести за знак определителя;2)Велечина определителя не изменится,если к элементу1 столбца прибавить элементы 2 столбца умножив на произвольное одинаковое число. Определители и их свойства 1. 2. 3.
Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали. Свойства: 1. Определитель не изменится, если его строки заменить столбцами, и наоборот. 2. При перестановке двух параллельных рядов определитель меняет знак. 3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю. 4. Общий множитель элементов можно вынести за знак определителя. 5. Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей. 6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число. 7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение. Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю. Определитель второго порядка вычисляется по формуле:
Определитель третьего порядка вычисляется по формуле:
Минор Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s. Алгебраическим дополнением элемента
где
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.197.182 (0.016 с.) |














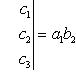




 матрицы
матрицы  называется число
называется число ,
, — дополнительный минор, определитель матрицы, получающейся из исходной матрицы
— дополнительный минор, определитель матрицы, получающейся из исходной матрицы 
 линейных уравнений с
линейных уравнений с  , то система имеет решение и притом единственное. Это решение задается формулами
, то система имеет решение и притом единственное. Это решение задается формулами 

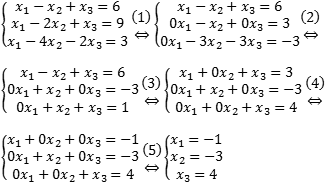

 , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
, называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.


 .
.




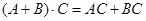




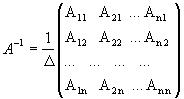
 называется наибольший из порядков миноров матрицы
называется наибольший из порядков миноров матрицы  Другими словами, решение СЛАУ находится с помощью обратной матрицы
Другими словами, решение СЛАУ находится с помощью обратной матрицы  . Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу
. Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу 
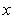



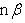


 - угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель
- угол наклона этого перпендикуляра к оси Ox. Чтобы привести общее уравнение прямой Ax + By + C = 0 к нормальному виду, нужно все члены его умножить на нормирующий множитель 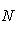


 , взятый со знаком, противоположным знаку свободного члена C.
, взятый со знаком, противоположным знаку свободного члена C.
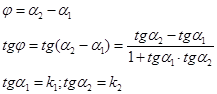




 и получим:
и получим: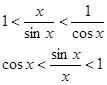
 , то по признаку существования пределов следует
, то по признаку существования пределов следует  .
.



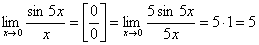 .
. .
.



 для
для  ,
, 

 .
. .
.
 и
и 








 [ c, d ]. Если функция f дифференцируема в точке х 0
[ c, d ]. Если функция f дифференцируема в точке х 0  [ a, b ], а функция g дифференцируема в точке y 0 = f (x 0)
[ a, b ], а функция g дифференцируема в точке y 0 = f (x 0) 
 такое, что f (b) - f (a) = f' (ξ)(b - a).
такое, что f (b) - f (a) = f' (ξ)(b - a).

 или
или  .
. и
и  , то
, то  ;
; и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения
 при условии существования предела
при условии существования предела  .
.

 при условии существования предела
при условии существования предела .
. при условии существования пределов
при условии существования пределов



 ), то наклонной асимптоты при
), то наклонной асимптоты при  (или
(или 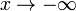 ) не существует!
) не существует! в п. 2.), то
в п. 2.), то  , и предел
, и предел 
 .
. .
. ,
,  , то есть:
, то есть: ,
, является искомым уравнением асимптоты.
является искомым уравнением асимптоты. , а функция g имеет производную в точке
, а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке
, то сложная функция h(x) = g(f(x)) также имеет производную в точке  где
где 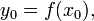 и
и  Пусть также эти функции дифференцируемы:
Пусть также эти функции дифференцируемы:  Тогда их композиция также дифференцируема:
Тогда их композиция также дифференцируема:  и её производная имеет вид:
и её производная имеет вид:
 где
где  принимает следующий вид:
принимает следующий вид:
 или f'x (x, у). Аналогично определяется и обозначается частная производная z по у.
или f'x (x, у). Аналогично определяется и обозначается частная производная z по у. 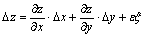 , (1)
, (1) при
при  .
.


