
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие вычисления и операции в MathcadСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ И ОПЕРАЦИИ В MATHCAD Цель работы: научиться производить расчёты простейших арифметических и алгебраических выражений. Порядок выполнения работы I. Вычислить значения арифметических выражений 25+
Если при вводе выражения была допущена ошибка, выделите неправильный символ угловой рамкой (щелкните мышью справа внизу возле символа), удалите выделенный символ (нажмите клавишу <Backspace>) и введите в помеченной позиции исправление. Mathcad читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее или ниже определенных для него значений переменных.
III. Определить функцию f(x) =
IV. Построить график функции f{t) =
* При вводе с клавиатуры символа <: > в рабочем документе отображается знак присваивания :=
Индивидуальные задания к лабораторной работе 1 I. Вычислить значения арифметических выражений:
II. Вычислить значение выражения:
III. Определить функцию f(x), вычислить ее значение при x=2,9 и построить таблицу значений функции для x [2;12] с шагом 1. Построить график функции.
1. Что такое табулирование функции? 2. Каково предназначение математического пакета MathCad? 3. Приведите простейший пример вычислительной задачи.
Литература: 1.Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2.Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3.Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4.Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5.Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
Порядок выполнения работы
I. Упростить выражение Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Большинство вычислений в Mathcad можно выполнить тремя способами выбором операции в меню, с помощью кнопочных панелей инструментов или обращением к соответствующим функциям. Преобразование алгебраических выражений В Mathcad можно выполнить следующие символьные преобразования алгебраических выражений: simplify (упростить) выполнить арифметические операции, привести подобные, сократить дроби, использовать для упрощения основные тождества (формулы сокращенного умножения, тригонометрические тождества и т.п.); expand (развернуть) раскрыть скобки, перемножить и привести подобные; factor (разложить на множители) представить, если возможно, выражение в виде произведения простых сомножителей; substitute (подставить) заменить в алгебраическом выражении букву или выражение другим выражением; convert to partial fraction разложить рациональную дробь на простейшие дроби. Если Mathcad не может выполнить требуемую операцию, то он выводит в качестве результата вычислений исходное выражение. Все приведенные вычисления выполнены в предположении, что в меню Math установлен автоматический режим вычислений и отключен режим оптимизации. Следует помнить, что Mathcad далеко не всегда преобразует выражение к самому простейшему виду.
<1> <+> <2> </> <3> <*> <x> <-> <1> Прежде чем вводить знак умножения и второй сомножитель, нажмите несколько раз клавишу <Space> (Пробел); нажимайте пробел до тех пор, пока весь первый сомножитель не будет заключен в выделяющую рамку. Затем введите знак умножения и второй сомножитель нажмите на клавиатуре клавиши в следующей последовательности:*
<*> <(> <1> <-> <9> <*> <х> <-> <9> <*> <х> <^> <2> <Space>... <Space> (выделить 9x-9x2) </> <3> <*> <х> <+> <1> <Space>... <Space> (выделить второй сомножитель) <+> <1>. Для того чтобы упростить введенное выражение, используйте меню символьных операций: щелкните справа внизу у последнего символа выражения и выделите его, нажимая клавишу <Space>. Затем щелкните в меню Symbolics по строке Simplify (рис. 31). Результат (преобразованное выражение) будет отображен в рабочем документе справа от исходного выражения.
Рис. 31. Процесс упрощения выражения через меню Symbolics
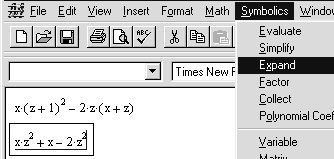
II. Раскрыть скобки и привести подобные в выражении x(z+1)2 - 2z(x+z). Указание. Сначала, как и в предыдущем примере, установите в меню Symbolics -- режим отображения результатов вычислений по горизонтали. Затем введите выражение для преобразования, выделите его и щелкните по строке Expand в меню Symbolics (рис.32). Результат (преобразованное выражение) отображается в рабочем документе справа от исходного выражения.
Рис.32. Упрощение выражений с использованием операции Expand. III. Разложить на множители выражение а2b + ab2 + 2abc + b2c+ +a2c+ ас2 + bc2. Указание. Введите выражение для преобразования, выделите его и щелкните по строке Factor в меню Symbolics. Результат отображается в рабочем документе справа от исходного выражения. При вводе выражения не забывайте вводить знак умножения (<*>), а после ввода показателя степени (<^>) нажимать клавишу <Space>. Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
Указание. Введите описанным выше способом выражение для преобразова-ний, выделите переменную х и щелкните по строке Convert to Partial Fraction в пункте Variable меню Symbolics. V. Построить таблицу значений функции f(x) = xsin Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.
* Запись <Space>... <Space> означает, что пробел нужно нажимать до тех пор, пока соответствующее выражение не будет заключено в выделяющую угловую рамку. Указание. Определите функцию f(x) = xsin
VI. Построить график функции f(x) =xsin
Указание. Определите функцию f(x), как в предыдущем примере, щелкните по свободному месту в рабочем документе правее и ниже определения функции f(x), затем щелкните по кнопке декартова графика VII. Решить графически уравнение f(x) = 0, где f(x) = x3+3x2-2. На рисунках 33 и 34 приведен фрагмент рабочего документа Mathcad с соответствующими определениями, графиками и окнами диалога. Указание. Определите функцию f(x) и постройте ее график, действуя, как в предыдущем примере. Для того чтобы найти корни уравнения абсциссы точек пересечения графика функции с осью у = 0, щелкните по строке Trace в пункте Graph меню Format. Затем щелкните по полю графиков и установите (стрелками клавиатуры или мышью) маркер (перекрещивающиеся пунктирные линии) в точке пересечения графика функции с осью абсцисс. В окне диалога отображаются координаты маркера: значение координаты х в окне и есть искомое приближенное значение корня.
Рис. 33. Определение координат на точки
VIII. Решить символьно уравнение Символьное решение этого уравнения в Mathcad занимает одну строчку.
Указание. Щелкните по кнопке решения уравнений
Порядок выполнения работы Задание. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы
Указание: 1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали. 2. Присвойте переменной ORIGIN значение, равное 1. 3. Введите матрицу и столбец правых частей. 4. Вычислите определитель матрицы. 5. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей. Указание. Для вычисления определителей D1, D2, D3, D4 проще всего скопировать матрицу А в буфер обмена (<Ctrl>+<C> или пункт Copy меню Edit), затем вставить в помеченной позиции матрицу из буфера обмена (<Ctrl>+<V> или пункт Insert меню Edit) и затем заменить элементы соответствующего столбца элементами столбца правых частей. 6.Найдите по формулам Крамера решение системы. Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Индивидуальные задания к лабораторной работе 3. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы Ах = B. 1. А = 2. A = 3. A = 4. A = 5. A = 6. A = 7. A =
9. A = 10. A = 11. A = 12. A = 13. A = 14. A = 15. A =
17. A = 18. A =
Содержание отчета 1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Назовите основные способы решения систем линейных уравнений. 2. Какие операторы позволяют осуществить решение систем нелинейных уравнений? 3. Для чего необходимо выполнять проверку решения уравнений? 4. В чем смысл решения уравнений численными методами? 5. Назовите порядок построения графика в декартовых системах координат. 6. Назовите порядок построения графика в полярной системе координат. Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с. Лабораторная работа 4
Цель работы: Освоить работу с процессом символьных вычислений на примере вычисления интегралов, производных, сумм, пределов. Изучить работу с векторами и матрицами. Задание: 1. По заданным координатам точек A, B, C, D найти координаты векторов a=AB и b=CD. 2. Вычислить скалярное и векторное произведения найденных векторов. 3. Найти следующие произведения векторов на заданную матрицу M: a*M и M*b. 4. Вычислить определитель матрицы M. 5. Для заданного ряда вычислить i -частичную сумму и исследовать сходимость ряда. 6. Вычислить сумму ряда. 7. Найти первообразную неопределенного интеграла и выполнить проверку, полученного результата. 8. Вычислить значения определенного интеграла. Пример выполнения задания: Задание:
1. Для выполнения задания 1 используем известную формулу из курса линейной алгебры, которая гласит, что координаты вектора численно равны разности координат точек конца и начала вектора:
Для этого в MathCAD точки A, B, C и D набираются в следующем виде:
Для чего открываем панель инструментов «Математика» (View\Toolbars\Math) и нажимаем на ней кнопку «Матрицы» ([MMM]) Далее задаем параметр i, меняющийся от 0 до 2 (для чего на панели «Матрица» есть кнопка вида “ m..n”). Примечание. Отметим, что в пакете MathCAD нумерация компонент векторов и элементов матриц начинается с 0:
Для просмотра координат векторов достаточно набрать «a=» и «b=». В данной задаче
Рекомендация: предлагаем читателю самостоятельно вычислить в MathCAD длину полученных векторов. 2. Вычислим скалярное и векторное произведение полученных векторов. Примечание. Обращаем внимание на то, что вычисление скалярного произведения в MathCAD осуществляется согласно правилу умножения матриц. В связи с этим вектора следует задавать следующим образом:
Примечание. Верхний индекс Т у вектора а означает операцию транспонирования и является результатом работы кнопки MT на панели «Матрица». Вычислим скалярное произведение:
Проверим результат, воспользовавшись определением скалярного произведения:
или в виде
Примечание. Если вектор задан в строчку, то MathCAD воспринимает его не как вектор, а как матрицу с одной строкой и n столбцами. Для набора нижнего индекса можно нажимать на клавиатуре кнопку [.
В качестве примера продемонстрируем проверку антикоммутативности векторного произведения
3. Рассмотрим произведение матрицы на вектор. Матрица задается с помощью встроенных функций пользователя, а произведение ее на вектор в MathCAD имеет вид:
Умножение вектора на матрицу осуществляется следующим образом:
4. Вычисление определителя матрицы выполняется с помощью встроенной символьной операции 5. Частичные суммы рядов вычисляются с помощью определенных символьных операций, представленных на рис. 1.
Рис. 1 Результаты вычислений имеют вид:
Примечание. Из курса математического анализа известно, что частичные суммы в теории рядов представляют собой отправную точку в исследовании их сходимости. Средства MathCAD позволяют, используя фундаментальное определение сходимости числового ряда, рассмотреть этот вопрос для различных числовых рядов. Здесь в качестве примера мы рассматриваем заданный выше ряд.
6. Ряд сходится, следовательно, можно вычислить его сумму:
7. Для вычисления неопределенных интегралов также используются встроенные символьные вычисления (см. рис. 1).
Примечание. Отметим, что в полученном результате отсутствует аддитивная постоянная. Согласно основному свойству интегралов производная от первообразной должна быть равна подынтегральной функции. Часто это свойство используется в качестве проверки полученных первообразных. Для вычисления производных снова используем встроенные символьные вычисления (см. рис. 1). В нашем случае получаем:
8. Для вычисления определенного интеграла, используя символьные операции, получаем
Примечание. Возможности пакета позволяют с помощью указанных символьных операций проводить исследования сходимости несобственных интегралов и изучение поведения разрывных функций на заданном интервале. 1.
1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы 1. Назовите способы выполнения символьных операций в MathCAD. 2. Что необходимо сделать с выражением перед применением символьных преобразований в командном режиме? 3. Перечислите символьные операции с выделенными выражениями. 4. Перечислите символьные операции с выделенными переменными. 5. Перечислите символьные операции с выделенными матрицами. 6. Перечислите символьные операции преобразования. 7. Какие параметры определяет стиль представления результатов вычислений и где он задается? 8. В каких случаях результат символьных преобразований помещается в буфер обмена? 9. Каким образом можно вычислить предел в MathCAD? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушако
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 9045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.172 (0.014 с.) |

 и 25+
и 25+  .
.



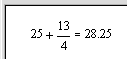



 II. Вычислить значение выражения, содержащего переменные:
II. Вычислить значение выражения, содержащего переменные: при t = 5, а = 9.8.
при t = 5, а = 9.8.



 , вычислить ее значение при х =1.2 и построить таблицу значений функции для х [0, 10] с шагом 1.
, вычислить ее значение при х =1.2 и построить таблицу значений функции для х [0, 10] с шагом 1.
 f( 1.2 )=.
Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2.
f( 1.2 )=.
Сразу после ввода знака равенства немедленно выводится вычисленное значение функции f(x) при х = 1.2.


 4. Щелкнув по свободному месту в рабочем документе, введите с клавиатуры f(x)=.
В результате под именем функции появится таблица значений функции.
4. Щелкнув по свободному месту в рабочем документе, введите с клавиатуры f(x)=.
В результате под именем функции появится таблица значений функции.

 .
.
 в панели математических инструментов и в открывшейся панели щелкните по кнопке.
в панели математических инструментов и в открывшейся панели щелкните по кнопке.  .
.



 Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.



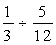








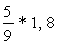






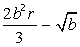 ,
при
,
при 
 ,
при
,
при 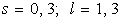
 ,
при
,
при 
 ,
при
,
при 
 , при
, при 
 , при
, при 
 ,
при
,
при 
 , при
, при 

 5.
5.
 ,
при
,
при 
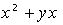 , при
, при 
 , при
, при 
 , при
, при 
 , при
, при 
 , при
, при 
 , при
, при 
 , при
, при 
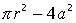 , при
, при 
 , при
, при 
 , при
, при 
 , при
, при 


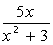







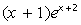

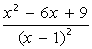
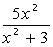
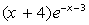
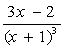

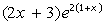
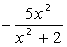

 Контрольные вопросы:
Контрольные вопросы: Лабораторная работа 2
Лабораторная работа 2



 IV. Разложить на простейшие дроби рациональную дробь
IV. Разложить на простейшие дроби рациональную дробь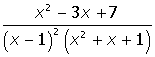

 на отрезке [0, 4p2].
на отрезке [0, 4p2].
 .Для этого введите с клавиатуры имя функции и имя аргумента, заключенное в круглые скобки, знак присваивания (введите с клавиатуры знак равенства или нажмите на клавиатуре клавиши <Shift>+<:> и следом выражение для функции. Чтобы ввести знак квадратного корня, щелкните в панели калькулятора по кнопке
.Для этого введите с клавиатуры имя функции и имя аргумента, заключенное в круглые скобки, знак присваивания (введите с клавиатуры знак равенства или нажмите на клавиатуре клавиши <Shift>+<:> и следом выражение для функции. Чтобы ввести знак квадратного корня, щелкните в панели калькулятора по кнопке  . Подкоренное выражение введите в позиции, указанной меткой. Знак абсолютной величины введите аналогично, щелчком по кнопке
. Подкоренное выражение введите в позиции, указанной меткой. Знак абсолютной величины введите аналогично, щелчком по кнопке  . Определите диапазон изменения индекса i узлов сетки хi на заданном отрезке. Для этого введите с клавиатуры: i == 0; 20*. Определите узлы сетки хi =
. Определите диапазон изменения индекса i узлов сетки хi на заданном отрезке. Для этого введите с клавиатуры: i == 0; 20*. Определите узлы сетки хi =  , для этого введите с клавиатуры: х [ i <Space> == i * 4 * (<Ctrl>+<p>)^2 <Space...Space> /20. Определите матрицу-столбец F для хранения таблицы значений функции в узлах сетки: Fi = f(xi). Для этого введите с клавиатуры: F [ i Space: f (х [ i <Space>). Чтобы вывести таблицу значения функции на экран, введите с клавиатуры: F =. В рабочем документе появится таблица значений функции. Щелкните по полю таблицы в рабочем документе откроется окно для просмотра всей таблицы со стрелками прокрутки.
, для этого введите с клавиатуры: х [ i <Space> == i * 4 * (<Ctrl>+<p>)^2 <Space...Space> /20. Определите матрицу-столбец F для хранения таблицы значений функции в узлах сетки: Fi = f(xi). Для этого введите с клавиатуры: F [ i Space: f (х [ i <Space>). Чтобы вывести таблицу значения функции на экран, введите с клавиатуры: F =. В рабочем документе появится таблица значений функции. Щелкните по полю таблицы в рабочем документе откроется окно для просмотра всей таблицы со стрелками прокрутки. .
.
 в панели графиков
в панели графиков  и введите в позиции, указанной меткой возле оси абсцисс, имя аргумента х, а возле оси ординат имя функции f(x). График будет построен после щелчка по рабочему документу вне поля графиков. Параметры изображения можно изменить, щелкнув дважды по полю графиков и определив параметры (вид отображения осей, толщину и цвет линии, надпись на графике).
и введите в позиции, указанной меткой возле оси абсцисс, имя аргумента х, а возле оси ординат имя функции f(x). График будет построен после щелчка по рабочему документу вне поля графиков. Параметры изображения можно изменить, щелкнув дважды по полю графиков и определив параметры (вид отображения осей, толщину и цвет линии, надпись на графике).




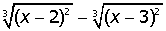 =0.
=0.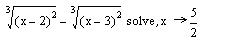
 в панели символьных вычислений
в панели символьных вычислений  . Введите в помеченной позиции слева от ключевого слова solve (решить) выражение для правой части уравнения, а в позиции справа от solve имя переменной, относительно которой нужно решить уравнение, и щелкните по свободному месту в рабочем документе. Результат значение корня уравнения будет отображен в рабочем документе справа от стрелки.
. Введите в помеченной позиции слева от ключевого слова solve (решить) выражение для правой части уравнения, а в позиции справа от solve имя переменной, относительно которой нужно решить уравнение, и щелкните по свободному месту в рабочем документе. Результат значение корня уравнения будет отображен в рабочем документе справа от стрелки.

 B =
B = 
 B =
B = 
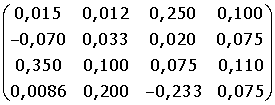 B =
B = 
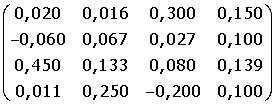 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 
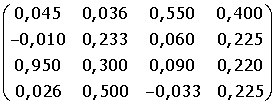 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 
 B =
B = 


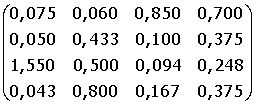 B =
B = 
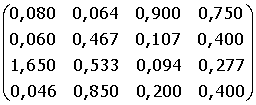 B =
B = 
 16. A =
16. A =  B =
B = 
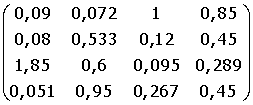 B =
B = 
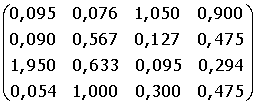 B =
B = 
 «Символьные вычисления»
«Символьные вычисления»


 . (1)
. (1)
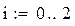
 Для нахождения координат наших векторов используем формулу (1), которая в MathCAD имеет вид:
Для нахождения координат наших векторов используем формулу (1), которая в MathCAD имеет вид:

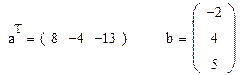

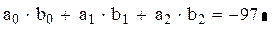
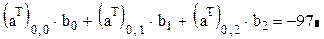
 Для вычисления векторного произведения вектора следует задавать в виде столбцов.
Для вычисления векторного произведения вектора следует задавать в виде столбцов.


 .
.








 2.
2.  при
при 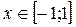
 Содержание отчета
Содержание отчета


