
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы в системе MathCadСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Численные методы в системе MathCad
Методические указания по выполнению лабораторных работ
Дисциплина – «Информатика» Специальности: 220301 «Автоматизация технологических процессов и производств» 140610 «Электрооборудование и электрохозяйства предприятий, организаций и учреждений» 151001 «Технология машиностроения»
Печатается по решению редакционно- Издательского совета ОрелГТУ
Орел 2008 Авторы: канд. эконом. наук, доц. каф. ПМиИ Н.П. Еремеева канд. эконом. наук, доц. каф. ПМиИ Е.В. Закалкина
Рецензент: канд. тех. наук, доц. каф. ПМиИ Л.А.Плетнева
Методические указания содержат теоретический материал о принципах работы в программе MathCad, краткие сведения из вычислительной математики, а также задания к лабораторным работам. Предназначены студентам, обучающимся по специальностям 220301 «Автоматизация технологических процессов и производств», 151001 «Технология машиностроения», 140610 «Электрообору-дование и электрохозяйства предприятий, организаций и учрежде-ний», изучающим дисциплину «Информатика». Данные методические указания могут быть также использованы для студентов других инженерных и экономических специальностей.
Редактор Ю.А. Демина Технический редактор В.В. Лях
Орловский государственный технический университет Лицензия ИД №00670 от 05.01.2000 г.
Подписано к печати 10.09.2008 г. Формат 60x84 1/16. Печать офсетная. Уч.-изд. л. 4,7. Усл. печ. л. 3,7. Тираж 15 экз. Заказ №________
Отпечатано с готового оригинал-макета в ООО «СтройИндустрияИнвест», 302020, г. Орел, Наугорское шоссе, 29.
© ОрелГТУ, 2008
СОДЕРЖАНИЕ Введение. 4 Лабораторная работа №1. 5 Основы работы в системе Mathcad. Построение графиков. 5 Лабораторная работа №2. 23 Решение систем уравнений. Решение нелинейных уравнений. 23 Лабораторная работа №3. 33 Приближение функций. 33 Лабораторная работа №4. 43 Численное интегрирование. Численное решение обыкновенных дифференциальных уравнений. 43 Список литературы.. 53 Приложение А.. 54 Приложение Б. 56 Приложение В.. 57 Приложение Г. 58 Приложение Д.. 59 Приложение Е.. 60 Приложение Ж... 61 Приложение З. 63
Практически во всех науках о природе, живой и неживой, об обществе построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многогранны и сложны, что лучшим способом их изучения часто является построение модели, отображающей лишь какую-то грань реальности и потому многократно более простой, чем эта реальность, и исследование этой модели. Модель является представлением объекта в некоторой форме, отличной от формы его реального существования. Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.
Возможности аналитических методов решения сложных математических задач очень ограничены, и, как правило, эти методы гораздо сложнее численных. Поэтому в данном практикуме приведены численные методы, реализуемые на компьютерах. Однако компьютеры при математическом моделировании используются не только для численных расчетов, но и для аналитических преобразований. Результат аналитического исследования математической модели часто бывает выражен столь сложной формулой, что при взгляде на нее невозможно представить описываемый процесс. Эту формулу нужно представить графически, проиллюстрировать в динамике. К программам, позволяющим выполнять такие задачи, относится система MathCad, которая представляет собой автоматизированную систему, позволяющую динамически обрабатывать данные в числовом и аналитическом (формульном) виде. Программа MathCad сочетает в себе возможности проведения расчетов и подготовки форматированных научных и технических документов. Данный лабораторный практикум содержит теоретический материал о принципах работы в программе MathCad, краткие сведения из вычислительной математики, а также задания к лабораторным работам. Целью выполнения заданий является получение и закрепление навыков решения прикладных задач с использованием программы MathCad. Лабораторная работа №1 Приемы работы с системой MathCad Документ программы MathCad называется рабочим листом. Он содержит объекты: формулы и текстовые блоки. В ходе расчетов формулы обрабатываются последовательно, слева направо и сверху вниз, а текстовые блоки игнорируются. Ввод информации осуществляется в месте расположения курсора. Программа MathCad использует три вида курсоров. Если ни один объект не выбран, используется крестообразный курсор, определяющий место создания следующего объекта. При вводе формул используется уголковый курсор, указывающий текущий элемент выражения. При вводе данных в текстовый блок применяется текстовый курсор ввиде вертикальной черты.
Ввод формул Формулы — основные объекты рабочего листа. Новый объект по умолчанию является формулой. Чтобы начать ввод формулы, надо установить крестообразный курсор в нужное место и начать ввод букв, цифр, знаков операций. При этом создается область формулы, в которой появляется уголковый курсор, охватывающий текущий элемент формулы, например имя переменной (функции) или число. При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд. Для управления порядком операций используют скобки, которые можно вводить вручную. Уголковый курсор позволяет автоматизировать такие действия. Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы. После ввода знака операции элементы в пределах уголкового курсора автоматически заключаются в скобки. Например, для ввода формулы
Элементы формул можно вводить с клавиатуры или с помощью специальных панелей управления. Панели управления (рисунок 1) открывают с помощью меню View (Вид) или кнопками панели управления Math (Математика). Для ввода элементов формул предназначены следующие панели: ° панель управления Arithmetic (Арифметика) для ввода чисел, знаков типичных математических операций и наиболее часто употребляемых стандартных функций; ° панель управления Evaluation (Оценка) для ввода операторов вычисления и знаков логических операций; ° панель управления Graph (График) для построения графиков; ° панель управления Matrix (Матрица) для ввода векторов и матриц и задания матричных операций; ° панель управления Calculus (Подсчет) для задания операций, относящихся к математическому анализу; ° панель управления Greek (Греческий) для ввода греческих букв (их можно также вводить с клавиатуры, если сразу после ввода соответствующего латинского символа нажимать сочетание клавиш CTRL+G, например [W][CTRL+G]-W); ° панель управления Symbolic (Символьный) для управления аналити-ческими преобразованиями.
Рисунок 1 - Панели инструментов программы MathCad
Введенное выражение обычно вычисляют или присваивают переменной. Для вывода результата выражения используют знак вычисления, который выглядит как знак равенства и вводится при помощи кнопки Evaluate Expression (Вычислить выражение) на панели инструментов Evaluation (Счет). Знак присваивания изображается как «:=», а вводится при помощи кнопки Assign Value (Присвоить значение) на панели инструментов Evaluation (Счет). Слева от знака присваивания указывают имя переменной. Оно может содержать латинские и греческие буквы, цифры, символы «’», «_», а также описательный индекс. Последний вводится с помощью символа «.» и изображается как нижний индекс, но является частью имени переменной, например Vmin. Индексы, определяющие отдельный элемент вектора или матрицы, задаются по-другому, с помощью символа «[».
Переменную, которой присвоено значение, можно использовать далее в документе в вычисляемых выражениях. Чтобы узнать значение переменной, следует использовать оператор вычисления. В следующем примере вычислена площадь круга с радиусом 2 (использованы переменные r и s, значение постоянной p определено в программе MathCad по умолчанию)
Ввод текста Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Текстовый блок создается нажатием кнопки с буквой А на панели инструментов или с помощью команды Insert > Text Region (Вставка > Текстовый блок). Иногда требуется встроить формулу внутрь текстового блока. Для этого служит команда Insert > Math Region (Вставка > Формула). Работа с матрицами Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне Insert Matrix (Вставка матрицы), которое открывают командой Insert > Matrix (Вставка > Матрица). Вектор задается как матрица, имеющая один столбец. После щелчка на кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение. При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обращении матриц и в декомпозиции (разложении в произведение матриц специального вида). Программа MathCad позволяет выполнить все эти операции с помощью стандартных математических операторов (сложение, умножение) или встроенных функций. Например:
Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы. Например, выражение М +3, где М — матрица, означает, что к каждому элементу матрицы прибавляется число 3. Если требуется явно указать необходимость поэлементного применения операции к матрице, используют знак векторизации, для ввода которого служит кнопка Vectorize (Векторизация) на панели инструментов Matrix (Матрица). Например:
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Для переопределения начала нумерации используют встроенную переменную ORIGIN. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).
Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М. Для его ввода используется кнопка Matrix Column (Столбец) на панели инструментов Matrix (Матрица). Чтобы задать общую формулу элементов матрицы, типа Мi,j:= i +j, используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через две точки значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например x:=0,0.01..1. Если разность прогрессии равна единице (то есть элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. Например, чтобы сформировать по приведенной выше формуле матрицу размером 6х6, перед этой формулой надо указать i:=0..5 j:=0..5. При формировании матрицы путем присвоения значений ее элементам размеры матрицы можно не задавать заранее. Всем неопределенным элементам автоматически присваиваются нулевые значения. Например, формула М5,5:= 1 создает матрицу М размером 6х6, у которой все элементы, кроме расположенного в правом нижнем углу, равны нулю. Построение графиков Чтобы построить двумерный график в координатных осях Х - У, надо дать команду Insert > Graph > X-Y Plot (Вставка > График > Декартовы координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют диапазон или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величины, но их можно задать и вручную. В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую. Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне. Текущий формат каждой линии приведен в списке, под которым расположены элементы управления, позволяющие изменять формат. Для построения трехмерного графика необходимо задать матрицу значений. Отобразить ее можно в виде поверхности, столбчатой диаграммы или линий уровня.
Задание 1.4 Построить график функции и поменять вид кривой на зеленый пунктир.
Порядок выполнения задания: 1. Введите функцию. 2. В панели математических знаков выбрать кнопку с изображением графика. 3. В палитре графиков щелкнуть на кнопке с изображением двумерного графика. 4. Ввести в место ввода шаблона по оси Х имя независимой переменной – х, а в место ввода шаблона по оси У имя зависимой переменной – у(х). 5. Нажать правую клавишу мыши на графике, выбрать меню Формат графика, во второй вкладке, появившегося окна изменить вид и цвет графика. Задание 1.5 Постройте график из задания 1.4 на интервале Порядок выполнения задания: 1. Задать функцию. 2. Задать количество точек, по которым строится график. 3. Вычислить значения аргумента 4. Построить график.
Задание 1.6 Построить график функции с условием на заданном интервале. Порядок выполнения задания: 1. Для задания функции с условием используйте функцию if: If(условие, выражение1если условие выполнено, выражение2 если условие не выполнено). 2. Для изменения интервала измените числа, стоящие в углах рамки графика по оси Х.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12. Задание 1.7 Построить графики функций из задания 1.4 и 1.6 в одной системе координат на интервале, указанном в задании 1.6. Порядок выполнения задания: 1. Задайте данные функции (обозначьте их, например f(x) и g(x)): 2. Вызвав шаблон графика, введите по оси Х имя независимой переменной (или переменных, если их несколько),по оси Y введите f(x), поставьте запятую (при этом первое выражение уходит вверх, а под ним появляется место ввода), введите g(x). 3. Отведя указатель мыши за пределы графика, щелкните левой кнопкой мыши – появится график с тремя кривыми.
Задание 1.8 Построить трехмерный график (поверхность)
Лабораторная работа №2 Итерационные методы Метод простой итерации. При решении итерационными методами каждая переменная системы находится как предел последовательности приближений. Систему линейных уравнений записывают в виде:
Далее выбирают начальные приближения значений переменных x1(0 ), x2(0),…, xn(0 ) (любые n чисел) и подставляя их в правую часть системы, находят следующие приближенные значения корней x1(1), x2(1),…, xn(1) и т.д. Итерационный процесс продолжается до тех пор, пока не выполнится условие:
Условие сходимости итерационного процесса:
Для решения систем линейных уравнений в системе MathCad существуют встроенные функции: augment(A,B) – формирует расширенную матрицу системы, в первых столбцах которой содержится матрица А, а в последних – матрица В; rref(A) – выполняет прямой и обратный ход метода Гаусса; submatrix(A,i,j,l,m) – формирует столбец решения системы (то есть формирует матрицу, которая является блоком матрицы А, расположенны в строках с i по j в столбцах с l по m). В системе MathСad также реализовано решение систем линейных и нелинейных уравнений итерационными методами. Для этого используются функции Given и Find (Приложение Б).
Задание 2.1. Исследуйте систему линейных уравнений и, если решение существует, найдите его по формулам Крамера. Вариант 1 1)
Вариант 2 1)
Вариант 3 1) Вариант 4 1)
Вариант 5 1)
Вариант 6 1)
Вариант 7 1)
Вариант 8 1)
Вариант 9 1) Вариант 10 1)
Вариант 11 1)
Вариант 12 1) Порядок выполнения задания: 1. Установите режим автоматического выполнения вычислений. 2. Введите матрицу системы. 3. Вычислите определитель матрицы системы. Система имеет единственное решение, если определитель отличен от нуля. 4. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей. 5. Найдите решение системы по формулам Крамера (2).
Задание 2.2. Решить систему уравнений задания 2.1 с помощью обратной матрицы. Порядок выполнения задания: 1. Введите матрицу системы и вектор-столбец правых частей. 2. Вычислите решение системы по формуле Х=А-1·В. 3. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.3. Решитьсистемулинейных уравнений задания 2.1 методом Гаусса.. Порядок выполнения задания: 1. Присвойте переменной ORIGIN значение, равное единице. 2. Введите матрицу системы и столбец правых частей. 3. Сформируйте расширенную матрицу системы. 4. Приведите расширенную матрицу системы к ступенчатому виду. 5. Сформируйте столбец решения системы. 6. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.4. Решить систему уравнений задания 2.1 с помощью встроенных функций Given и Find. Порядок выполнения задания: 1. Записать служебное слово Given. 2. Ввести систему уравнений. 3. Вывести решение с помощью функции Find.
Задание 2.5. Решитьсистемулинейных уравнений методом простых итераций.
Вариант 1 A =
Вариант 2 A = Вариант 3 A = Вариант 4 A = Вариант 5 A = Вариант 6 A = Вариант 7 A = Вариант 8 A = Вариант 9 A =
Вариант 10 A = Вариант 11 A = Вариант 12 A =
Порядок выполнения задания: 1. Преобразуйте исходную систему Сх=d к виду х=B+Ах. 2. Проверьте достаточное условие сходимости. 3. Введите матрицы А и B. 4. Определите нулевое (начальное) приближение решения. 5. Задайте количество итераций. 6. Введите формулу вычисления последовательных приближений решения и вычислите их. 7. Выведите на экран матрицу приближенных решений. Метод хорд При решении уравнения методом хорд отрезок [ a,b ], которому принадлежит корень уравнения, делится не пополам, а в отношении, пропорциональном отношению абсолютных величин значений функции на концах отрезка. Геометрически это означает, что очередное приближение корня уравнения с – это точка пересечения с осью OX хорды, проходящей через крайние точки дуги кривой f(x):
Метод касательных Пусть на [ a,b ] функция f меняет знак, но сохраняет знаки своих первой и второй производных. В качестве нулевого приближения корня уравнения x0 выбирается тот из концов отрезка [ a,b ], которому отвечает значение функции f(x0) того же знака, что и знак второй производной f'''(x0). Проведем касательную к графику функции f(x) в точке (x0, f(x0)) и точку пересечения ее с осью OX возьмем в качестве первого приближения:
Очередные приближения можно найти аналогично:
Метод простой итерации Для использования данного метода уравнение записывается в виде: x = f(x). (8)
Подставляя начальное приближение в правую часть уравнения, получаем новое приближение: cn+1 = f(cn)n = 1, 2, … (9)
Достаточное условие сходимости f '(cn) < 1. Для решения нелинейных уравнений в системе MathCad существуют встроенные функции, приведенные в приложении. При использовании функции root, необходимо задать начальное приближение корня. Для отыскания корней полинома можно использовать функцию polyroot, задав перед этим вектор коэффициентов. Задание 2.6. Найти все корни уравнения (таблица 1).
Таблица 1 – Задания для расчетов
Лабораторная работа №3 Приближение функций Интерполирование функций При математическом моделировании часто используются зависимости вида у(х), обычно заданные рядом значений х и у их узловых точек. Однако, когда этих точек мало, такая зависимость оказывается не информативной и не наглядной. Промежуточные точки зависимости у(х) можно получить путем их интерполяции. Интерполирующая функция должна проходить через узловые точки и принимать значения, близкие к точным, в остальных точках. Одной из распространенных интерполирующих функций является интерполяционный многочлен Лагранжа:
При n=1 получается формула линейной интерполяции, при n=2 – квадратичной интерполяции и т.д. В системе MathCad существуют встроенные функции линейной и сплайн-интерполяции. При линейной интерполяции узловые точки соединяются отрезками прямых. Если х выходит за пределы конечных точек, то осуществляется линейная экстраполяция по отрезкам прямых, примыкающим к конечным точкам. При сплайн-интерполяции зависимость у(х) заменяется кусками полиномов третьей степени. Каждый полином проходит точно через три ближайшие узловые точки. Коэффициенты полинома подбираются так, чтобы обеспечить не только непрерывность функции в узловых точках, но и непрерывность ее двух производных. Эти свойства сплайн-интерполяции позволяют эффективно применять ее даже при малом числе узловых точек – до 5-7 для простых функций. Интерполяция реализуется с помощью следующих функций: - linterp(X,Y,x) –вычисляет значение у(х) для заданного х при линейной интерполяции, - cspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и кубической экстраполяции, - pspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и параболической экстраполяции, - lspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и линейной экстраполяции, - interp(V,X,Y,x) – вычисляет значение у(х) для заданного х при сплайн-интерполяции.
Задание 3.1. Определить значения функции в точках Х1 и Х2, используя встроенные функции линейной и сплайн-интерполяции. Построить графики интерполирующих функций в обоих случаях (см. приложение В).
Вариант 1
Х1=5,2 Х2=7,9
Вариант 2
Х1=2,1 Х2=7,3
Вариант 3
Х1=4,1 Х2=7,9
Вариант 4
Х1=3,9 Х2=9,3
Вариант 5
Х1=2,9 Х2=7,4
Вариант 6
Х1=5,5 Х2=9,4
Вариант 7
Х1=2,5 Х2=8,3
Вариант 8
Х1=4,1 Х2=7,2
Вариант 9
Х1=2,8 Х2=9,1
Вариант 10
Х1=4,1 Х2=8,2
Вариант 11
Х1=2,9 Х2=7,1
Вариант 12
Х1=5,5 Х2=8,9
Порядок выполнения задания: 1. Ввести значения векторов Х и У. 2. С помощью функции linterp(X,Y,x) найти значения функции у(х) в заданных точках х при линейной интерполяции. 3. Построить график функции при линейной интерполяции. 4. С помощью функций cspline(X,Y) interp(V,X,Y,x) найти значения функции у(х) в заданных точках х при сплайн-интерполяции. 5. Построить график функции при сплайн-интерполяции.
Задание 3.2. Записать интерполяционный многочлен Лагранжа и вычислить значения функции в указанных точках с помощью системы MathCad. Построить график.
Порядок выполнения задания: 1. Записать формулу интерполяционного многочлена Лагранжа, используя знаки суммы и произведения и встроенной функции if (условие, выражение 1, выражение 2), которая принимает значение выражения 1, если условие выполняется, и выражения 2, если условие не выполняется. 2. Вычислить значение функции в указанных точках (данные взять из задания 1). 3. Построить график интерполяционного многочлена.
Задание 3.3 По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа (19).
Вариант 1
Вариант 2
Вариант 3
Вариант 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 648; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.171.137 (0.015 с.) |

 необходимо набрать
необходимо набрать 
 затем нажать пробел и ввести
затем нажать пробел и ввести  . Для ввода формулы
. Для ввода формулы  , записать
, записать  нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести
нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести  .
.








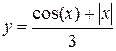



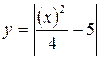







 по 50 точкам.
по 50 точкам.





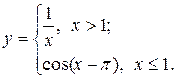







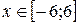

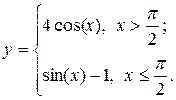










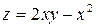




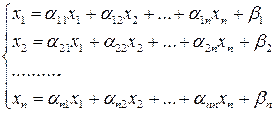 (3)
(3) k = 1,…,n
k = 1,…,n (4)
(4) 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 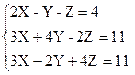
 2)
2) 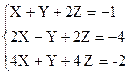
 2)
2) 
 2)
2) 
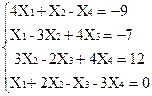 2)
2) 
 2)
2) 
 2)
2) 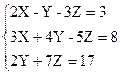
 , B =
, B = 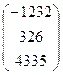
 , B =
, B = 
 , B =
, B = 
 , B =
, B = 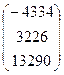
 , B =
, B = 
 , B =
, B = 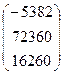
 , B =
, B = 
 , B =
, B = 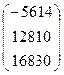
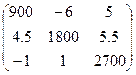 , B =
, B = 
 , B =
, B = 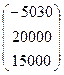
 , B =
, B = 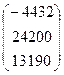
 , B =
, B = 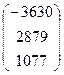
 . (5)
. (5)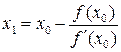 (6)
(6) ; n=0, 1, 2… (7)
; n=0, 1, 2… (7) . (19)
. (19)


