
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез лінійної безперервної частини системи управлінняСодержание книги
Поиск на нашем сайте
Розглянемо розрахунок динамічної системи автоматичного управління із заданими показниками якості на конкретному прикладі. Нехай структурна схема суднової системи управління має вигляд:
Передаточні функції структурних елементів суднової системи управління:
Значення параметрів системи:
Задані якісні показники системи:
Необхідно розрахувати корегуючий пристрій, що забезпечував би заданій судновій системі управління, необхідні якісні показники. Виходячи з цього, структурна схема проектованої суднової системи управління матиме вигляд:
2.1.1 Приведення структурної схеми до робочого вигляду У початковій структурній схемі слід замінити кожен коефіцієнт Разом з базовою структурною схемою буде необхідна інша, яка береться за робочу, вона матиме вигляд:
Де Розглянемо розімкнену систему:
Таким чином, передаточна функція розімкненої системи відповідно до правил структурних перетворень має вигляд:
Робоча структурна схема системи і канонічний запис передаточної функції розімкненої системи є початковою для подальших розрахунків частотним методом. Передаточна функція замкнутої системи управління відповідно до робочої структурної схеми має вигляд:
За коренями характеристичного рівняння (знаменника отриманої передаточної функції) можна визначити стійкість початкової нескорегованої системи. Так корені знаменника:
Оскільки два уявні корені знаменника мають дійсну частину більше нуля (останні менше нуля), то початкова нескорегована система є нестійкою. Нестійкість початкової системи показує і побудований в програмі Mathcad графік перехідного процесу (рис. 14).
2.1.2. Побудова ЛАЧХ початкової системи автоматичного управління. За канонічним видом передаточної функції можна визначити зразковий вид логарифмічної амплітудно-частотної характеристики (ЛАЧХ). Для цього необхідно знайти коефіцієнт підсилення і постійні часу з виразу для передаточної функції розімкненої системи (2.1.1).
Частоти, що сполучаються, визначаються із співвідношення
Коефіцієнт підсилення на частоті
Перед побудовою ЛАЧХ слід вибрати і розмістити систему координат. Тут потрібно мати на увазі наступне: 1) по осі ординат розбиття йде рівномірно, в децибелах: 0 дБ, 20 дБ, 40 дБ − вгору і -20 дБ, -40 дБ... – вниз. 2) по осі абсцис розбиття йде логарифмічне, але оцифрування в звичайному вигляді:...0,1 c-1, 1 с-1, 10 с-1, 100 с-1 і так далі. 3) початок осі координат рекомендується помістити в точку, віддалену на 3-4 декади ліворуч від самої найменшої частоти, що сполучає (яка відповідає максимальній постійній часу в канонічному записі передаточної функції розімкненої системи). 4) при побудові фазової характеристики вісь абсцис залишається тією ж самою, вісь ординат з початку системи координат прямує вниз, розбиття її рівномірне в градусах (від’ємних): 0 град, -90 град, -180 град і так далі. Підставимо в передаточну функцію
Побудова ЛАЧХ проводиться наступним чином: На частоті Вид ЛАЧХ, побудованої в програмі Mathcad за канонічним виглядом передаточної функції, представлений на рис. 15. Передаточна функція нескорегованої системи в канонічній формі має вигляд:
Тоді фазова характеристика системи управління визначається за допомогою формули:
Таким чином, отримаємо:
2.1.3 Побудова бажаної ЛАЧХ САУ Найбільш відповідальним етапом синтезу корегуючого пристрою є етап побудови бажаної ЛАЧХ. Він заснований на зв’язку перехідного процесу з дійсною частотною характеристикою замкнутої системи і ЛАЧХ розімкненої системи. Для вибору корегуючих пристроїв за заданими показниками якості перехідного процесу необхідно мати в своєму розпорядженні частотні характеристики, які повинні бути побудовані відповідно до вимог, пред’явлених до динамічних властивостей системи. Процес побудови бажаних частотних характеристик в значній мірі спрощується, якщо існують залежності, що встановлюють зв’язок між основними параметрами частотних характеристик, з одного боку, і показниками якості процесу регулювання – з іншого. У довідковій літературі [3], [16] представлені характеристики часу регулювання і перерегулювання (рис. 8). Сполучаючі частоти, що визначають тривалість середньочастотної ділянки, знаходяться виходячи із заданого запасу стійкості, який встановлюється за Виходячи із заданої величини перерегулювання
За відомим співвідношенням визначається частота зрізу
Отримані величини дозволяють побудувати низькочастотну і середньочастотну частини бажаної ЛАЧХ (БЛАЧХ). Виберемо злами БЛАЧХ на рівні 0.394 с-1 та 188.049 с-1. Таким чином, складові частини БЛАЧХ мають нахил 0: -20: -80 дБ/ дек. Виходячи з властивості логарифмічної функції:
ЛАЧХ корегуючого пристрою може бути отримана за наступним виразом:
ЛАЧХ корегуючого пристрою, має нахили 0:-20:0:+40:+60:0 дБ/ дек. Всі характеристики будуються для розімкненої динамічної системи управління.
2.1.4 Знаходження передаточної функції корегуючого пристрою На підставі бажаної і початкової ЛАЧХ системи визначається ЛАЧХ послідовного корегуючого пристрою. Якщо бажану передаточну функцію системи позначити через
звідки
і для ЛАЧХ отримаємо:
Таким чином, ЛАЧХ корегуючої ланки отримується простим відніманням ординат нескорегованої ЛАЧХ з ординат бажаної. Розглянемо першу корегуючу ланку (рис. 18), яка забезпечить злам на -20 дБ/дек.
Параметри інтегруючої ланки: 1) Передаточна функція ланки має вигляд
2) постійні часу
3) Амплітудна і фазова характеристики визначаються наступним чином:
Розрахуємо параметри елементів інтегратора. Інтегратор має частоти зламів ЛАЧХ, що дорівнюють:
Виберемо стандартні значення Розглянемо другу корегуючу ланку (рис. 19), що забезпечить злам на +20 дБ/дек.
Для диференціюючого кола основні співвідношення мають наступний вигляд: 1) Передаточна функція ланки:
2) постійні часу
3) Амплітудна і фазова характеристики визначаються таким чином:
Розрахуємо параметри елементів першого диференціатора. Частоти зламів дорівнюють:
Виберемо стандартні значення Розрахуємо другий диференціатор за аналогічною схемою. Частоти зламів дорівнюють
Виберемо стандартні значення Розрахуємо третій диференціатор за аналогічною схемою. Частоти зламів дорівнюють:
Виберемо стандартні значення Знайдемо постійні часу корегуючих кіл з урахуванням вибору реальних номіналів електрорадіоелементів:
Таким чином, інтегруюча і диференціююча частини корегуючого пристрою матимуть наступні передаточні функції, відповідно:
Виходячи з наведених передаточних функцій окремих ланок КП, передаточна функція корегуючого пристрою матиме вигляд:
Для послідовного з’єднання пасивних ланок необхідно мінімізувати їх взаємний вплив. Для цього зазвичай використовують буферні неінвертуючі підсилювачі з одиничним коефіцієнтом підсилення і широкою смугою пропускання. Виберемо інтегральні операційні підсилювачі, включені за неінвертуючою схемою з 100 % від’ємним зворотним зв'язком (ВЗЗ). Схема такого підсилювача зображена на рис. 20. Резистор в ланцюзі зворотного зв’язку обирається для конкретного операційного підсилювача. Вибір типу операційного підсилювача не входить до змісту даної курсової роботи.
Для технічної реалізації корегуючого пристрою необхідні послідовно сполучені інтегратор і три диференціатори. Принципова схема пристрою корекції зображена на рис. 21, а підсумкова схема корегуючого пристрою, що включає буферні підсилювачі, – на рис. 22.
2.1.5 Оцінка якості скорегованої САС Передаточна функція розімкненої системи управління з урахуванням корегуючого пристрою має наступний вигляд:
Передаточна функція замкнутої системи визначається як:
Для оцінки якості скорегованої системи необхідно побудувати перехідну характеристику – реакцію замкнутої системи з корегуючою ланкою на вхідну ступінчасту дію. Вона визначатиметься як:
Перехідна характеристика системи, визначена в програмі Mathcad. Графік перехідного процесу в скорегованій системі зображено на рис. 23. Пунктирними лініями вказана 5% зона відхилення вихідної величини від сталого значення, оскільки задана статична помилка −
З графіка перехідного процесу можна визначити параметри, що визначають якість процесу управління, а саме: 1) час регулювання 2) перерегулювання Технічне завдання передбачає максимальний час регулювання (час, за який перехідний процес увійде до 5% зони відхилення від сталого значення і вже не вийде з неї після цього) рівним 0.9 с. Таким чином, отриманий параметр В завданні також вказується, що максимальна величина перерегулювання (частка амплітуди максимального викиду перехідного процесу над сталим значенням від величини амплітуди сталого режиму системи управління) дорівнює 18 %. Отриманий параметр Таким чином, за допомогою синтезу послідовного корегуючого пристрою була отримана система управління із заданими характеристиками.
Синтез дискретної системи Завдання ЦОМ [12] (цифрової обчислювальної машини) полягає в забезпеченні бажаних динамічних характеристик системи управління за допомогою використання в ЦОМ програм, що коректують. У цьому випадку ЦОМ є по суті цифровий фільтр із заданими характеристиками. Цифрові системи управління мають квантування за часом, що відносить їх до класу дискретних (імпульсних) систем, і квантування за рівнем (у аналого-цифрових і цифро-аналогових перетворювачах). Якщо розрядність вхідних і вихідних перетворювачів достатньо велика, то їх нелінійністю можна нехтувати, при цьому розглядається лінеаризована дискретна система з урахуванням впливу, що надається квантуванням за рівнем, у вигляді додаткового шуму квантування, що розглядається як випадковий процес з рівноімовірним законом розподілу. Спрощену структурну схему цифрової системи подано на рис. 24. Безперервний сигнал похибки
На виході формувача імпульсів протягом усього періоду квантування
або, через те що
Передаточна функція приведеної безперервної частини системи визначається за формулою
а її дискретна передаточна функція – за формулою:
Якщо в каналі керування є затримка часу
2.2.1 Дискретна передаточна функція безперервної частини Основною засадою у визначенні дискретної передаточної функції безперервної частини є вибір періоду дискретизації за допомогою теореми Котельникова, яка дозволяє відповісти на питання, як за допомогою одиничних імпульсів передати без спотворення інформацію, що міститься в безперервному сигналі, і яка при цьому повинна бути частота проходження імпульсів. Згідно цій теоремі, безперервна функція Таким чином, період дискретизації дорівнює:
Наступним кроком синтезу дискретної системи є перетворення передаточної функції безперервної частини системи управління в імпульсну, використовуючи програму Mathcad. Для цього необхідно отримати решітчасту функцію шляхом застосування зворотного перетворення Лапласа і заміни змінної
2.2.2 Дискретна передаточна функція корегуючої ланки Аналогом розрахованої раніше безперервної корегуючої ланки в дискретній системі є ЦОМ. Для визначення її передаточної функції необхідно перетворити передаточну функцію корегуючого пристрою в Таким чином, передаточна функція ЦОМ має вигляд:
Враховуючи, що передаточна функція ЦОМ
Отже, розділивши чисельник і знаменник на
На підставі знайденої функції
де Таким чином, закон управління має вигляд:
Дане рівняння відіграє роль алгоритму роботи ЦОМ, що є дискретним фільтром з передаточною функцією
2.2.3 Дискретна передаточна функція замкнутої системи Загальна дискретна передаточна функція розімкненої системи знаходиться, використовуючи наступну формулу:
Дана формула застосовується, оскільки дискретний фільтр та екстраполятор розділені ключовим елементом. Тоді дискретна передаточна функція замкнутої системи матиме вигляд:
2.2.4 Аналіз синтезованої дискретної системи Раніше зазначалося, що якісний аналіз спроектованої суднової автоматичної системи починається з визначення стійкості системи. Стійкість замкнутою цифрової САС визначається видом коренів характеристичного рівняння. У стійкій цифровій системі корені характеристичного рівняння У даному прикладі курсової роботи корені характеристичного рівняння дорівнюють:
Модуль кожного кореня менше одиниці, отже, дискретна САС стійка. Наступним етапом аналізу синтезованої системи є визначення якісних показників за виглядом перехідного процесу. Графік перехідного процесу може бути отриманий шляхом моделювання системи в програмі MATLAB (пакет Simulink) (рис. 25, 26).
За графіком перехідного процесу можна визначити параметри, що характеризують якість процесу управління, а саме: 1) час регулювання: Значення даного параметра задовольняє технічному завданню. 2) максимальне перерегулювання динамічної системи: Отримане значення перерегулювання повністю задовольняє технічному завданню і має запас по чисельному значенню.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.012 с.) |

 − задаюча дія;
− задаюча дія;  − вихідна величина системи управління.
− вихідна величина системи управління.



 − передаточна функція корегуючого пристрою;
− передаточна функція корегуючого пристрою;  − передаточна функція розімкненої нескорегованої (заданої) системи управління.
− передаточна функція розімкненої нескорегованої (заданої) системи управління.
 його конкретним виглядом, відповідно до завдання. Така структурна схема вважатиметься базовою при виконанні першої частини роботи.
його конкретним виглядом, відповідно до завдання. Така структурна схема вважатиметься базовою при виконанні першої частини роботи.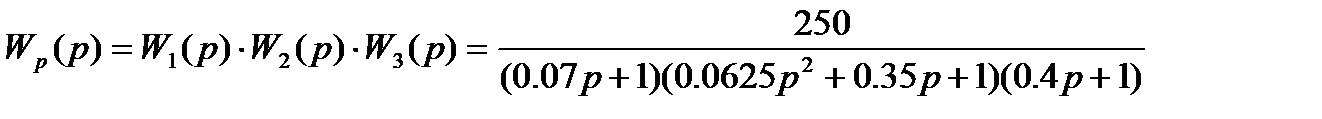



 :
:
 дорівнюватиме:
дорівнюватиме:
 і запишемо її у вигляді:
і запишемо її у вигляді:
 відкладаємо значення 20 lg (250) = 48 дБ та через цю точку проводимо пряму з нахилом
відкладаємо значення 20 lg (250) = 48 дБ та через цю точку проводимо пряму з нахилом  , до частоти
, до частоти  . Далі проводимо пряму з нахилом
. Далі проводимо пряму з нахилом  , що відповідає ланці
, що відповідає ланці  до частоти
до частоти  . Далі пряма з нахилом
. Далі пряма з нахилом  , що відповідає ланці
, що відповідає ланці 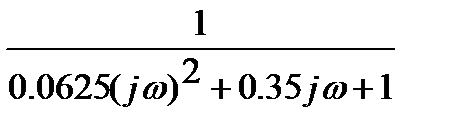 . Далі пряма з нахилом
. Далі пряма з нахилом  , що відповідає ланці
, що відповідає ланці  .
.




 , виходячи з побудованого довідкового графіка.
, виходячи з побудованого довідкового графіка. за номограмою (рис. 7, а) визначається
за номограмою (рис. 7, а) визначається  і співвідношення для
і співвідношення для  . За відомим заданим часом регулювання
. За відомим заданим часом регулювання  можна визначити мінімальну циклічну частоту
можна визначити мінімальну циклічну частоту  :
: .
.
 :
: .
.
 ,
,
 .
.

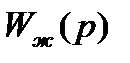 , передаточну функцію початкової системи (нескорегованої) −
, передаточну функцію початкової системи (нескорегованої) − 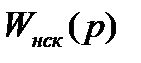 , а корегуючої ланки -
, а корегуючої ланки -  , то можна записати наступний вираз:
, то можна записати наступний вираз: ,
,

 .
.
 ;
;
 знаходяться за частотами:
знаходяться за частотами: 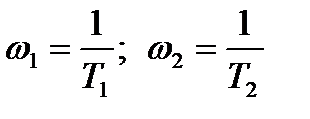 і визначають параметри елементів
і визначають параметри елементів  корегуючого пристрою:
корегуючого пристрою:



 .
.

 . Виберемо стандартний конденсатор
. Виберемо стандартний конденсатор  мФ, оскільки частоти зламів невеликі. Резистори повинні мати наступні параметри:
мФ, оскільки частоти зламів невеликі. Резистори повинні мати наступні параметри: Ом;
Ом;  Ом.
Ом.
 Ом;
Ом;  Ом (з ряду Е96).
Ом (з ряду Е96). ;
;




 .
.

 . Виберемо стандартний
. Виберемо стандартний  мкФ, оскільки частоти зламів невеликі. Резистори повинні мати наступні параметри:
мкФ, оскільки частоти зламів невеликі. Резистори повинні мати наступні параметри: Ом;
Ом;  Ом.
Ом.
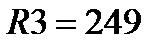 Ом
Ом  Ом (з ряду Е96).
Ом (з ряду Е96).
 . Виберемо стандартний
. Виберемо стандартний  мкФ. Резистори матимуть наступні параметри:
мкФ. Резистори матимуть наступні параметри: Ом
Ом  Ом.
Ом.
 Ом;
Ом;  Ом (з ряду Е96).
Ом (з ряду Е96). ;
; 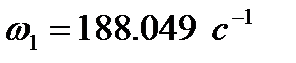 . Виберемо стандартний
. Виберемо стандартний  мкФ. Резистори матимуть наступні параметри:
мкФ. Резистори матимуть наступні параметри: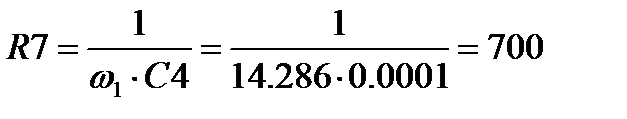 Ом;
Ом;  Ом.
Ом.
 Ом;
Ом; 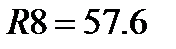 Ом (з ряду Е96).
Ом (з ряду Е96). ;
;  ;
;  ;
; 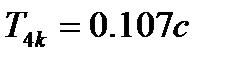 ;
;
 ;
;  ;
;  ;
;  .
.
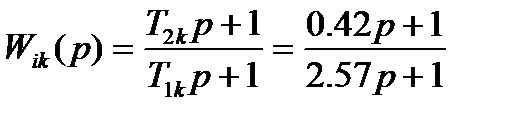 ;
;
 .
.
 .
.
 ,
,
 .
.
 ,
,
 .
.

 .
.
 , що задовольняє заданому у технічному завданні значенню;
, що задовольняє заданому у технічному завданні значенню; , що задовольняє заданому у технічному завданні значенню.
, що задовольняє заданому у технічному завданні значенню. відповідає технічному завданню.
відповідає технічному завданню. імпульсним елементом ІЕ1перетворюється в решітчасту цифрову функцію
імпульсним елементом ІЕ1перетворюється в решітчасту цифрову функцію  і надходить на вхід ЦОМ, яку подано у вигляді передаточної функції
і надходить на вхід ЦОМ, яку подано у вигляді передаточної функції  . Вихідний сигнал ЦОМ імпульсним елементом ІЕ2і формувачем (екстраполятором)
. Вихідний сигнал ЦОМ імпульсним елементом ІЕ2і формувачем (екстраполятором)  перетворюється в ступінчастий сигнал. Безперервну частину системи подано ланкою з передаточною функцією
перетворюється в ступінчастий сигнал. Безперервну частину системи подано ланкою з передаточною функцією  .
. зберігається попереднє значення сигналу, тому формувач є фіксатором (екстраполятором) нульового порядку. Його передаточна функція має вигляд
зберігається попереднє значення сигналу, тому формувач є фіксатором (екстраполятором) нульового порядку. Його передаточна функція має вигляд ,
,
 ,
, .
.
 ,
,
 .
.
 , то попередній вираз запишеться у вигляді
, то попередній вираз запишеться у вигляді .
.
 , наприклад, сигнал задавання
, наприклад, сигнал задавання  , частотний спектр якого обмежений частотами від
, частотний спектр якого обмежений частотами від 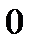 до
до  , повністю відтворюється дискретним сигналом
, повністю відтворюється дискретним сигналом  , якщо задовольняється умова
, якщо задовольняється умова  або
або  , с. Фізичний сенс такого ствердження визначається тим, що неперервна функція, яка не містить у своєму спектрі частот, що перевищують
, с. Фізичний сенс такого ствердження визначається тим, що неперервна функція, яка не містить у своєму спектрі частот, що перевищують  , рівний половині періоду найбільшої частоти
, рівний половині періоду найбільшої частоти  .
.
 добутком
добутком  . Після цього до решітчастої функції застосовується
. Після цього до решітчастої функції застосовується  - перетворення, в результаті передаточна функція безперервної частини системи в
- перетворення, в результаті передаточна функція безперервної частини системи в  .
.
 .
.
 є відношенням зображень вихідної і вхідної величин, узятих в цифровій формі, то отримаємо вираз:
є відношенням зображень вихідної і вхідної величин, узятих в цифровій формі, то отримаємо вираз: .
.
 отримаємо
отримаємо .
.
 можна отримати закон управління, ЦОМ, що реалізується, у вигляді рекурентного різницевого рівняння. Для цього необхідно перейти від передаточної функції ЦОМ до оригіналів, в результаті отримаємо:
можна отримати закон управління, ЦОМ, що реалізується, у вигляді рекурентного різницевого рівняння. Для цього необхідно перейти від передаточної функції ЦОМ до оригіналів, в результаті отримаємо: ,
,
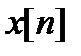
 .
.
 .
. .
.
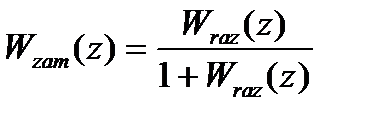 ,
,
 .
.
 повинні лежати усередині кола одиничного радіусу, тобто бути по модулю менше одиниці.
повинні лежати усередині кола одиничного радіусу, тобто бути по модулю менше одиниці. ,
,  ,
,  ,
,  .
.


 .
. .
.


