
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез корегуючих пристроїв. Методика побудови бажаної логарифмічно-амплітудної характеристикиСодержание книги
Поиск на нашем сайте Найбільше застосування отримали частотні методи вибору корегуючих кіл згідно заданим технічним вимогам. При цьому можуть бути застосовані два частотні методи: 1) метод, заснований на використанні логарифмічних частотних характеристик; 2) метод, заснований на використанні амплітудно-фазових характеристик. Найбільшою простотою та інженерною закінченістю відрізняється метод логарифмічних характеристик. Проектування САС відповідно до заданих технічних вимог (ТВ) включає: синтез САС за умови фізичної реалізації автоматичної системи і раціонального вибору її елементів та синтез корегуючих кіл, що забезпечує задоволення заданих вимог якості до скоректованої САС. Синтез корегуючої ланки полягає у виборі її вигляду, визначенні передаточної функції, розрахунку параметрів кола, з тим щоб проектована САС мала задані за ТВ показники якості: час перехідного процесу Залежно від конкретних умов роботи САС виділяють основні вимоги до проектованої системи. Наприклад, якщо для системи основним є режим стеження, то головними будуть вимоги до точності в сталому режимі; якщо САС працює в динамічному режимі, то основними будуть вимоги до якості перехідного процесу тощо. Таким чином, синтез зводиться до визначення логарифмічної характеристики ідеальної САС відповідно до заданих ТВ. Ця характеристика отримала назву бажаної логарифмічно-амплітудної характеристики (БЛАХ) (рис. 7).
При побудові БЛАХ на всьому діапазоні частот слід виділяти три основні ділянки – низькочастотну, середньочастотну і високочастотну. Низькочастотна ділянка визначає точність роботи САС в сталому режимі. Ця ділянка відповідає області частот, які менше першої частоти, що сполучає
де Середньочастотна ділянка визначає основні динамічні якості САС. Від правильного вибору діапазону частот цієї ділянки залежить час регулювання Високочастотна ділянка, що характеризується інтервалом частот Важливим моментом побудови БЛАХ є правильне сполучення трьох ділянок. При сполученні завжди слід брати до уваги вид логарифмічної характеристики нескорегованої САС, побудованої з умов фізичної реалізації системи. Чим менше БЛАХ відрізнятиметься від ЛАХ нескорегованої САС, тим простіше вид логарифмічної характеристики корегуючої ланки. Таким чином, вибір БЛАХ зводиться до наступної послідовності операцій: 1. Будують ЛАХ нескорегованої САС, використовуючи всі можливості попереднього структурного аналізу для отримання кращих якісних характеристик. 2. Відповідно графіку (рис. 8,а) за вхідною величиною
3. За номограмою (рис. 8, б), використовуючи необхідне значення 4. За графіком (рис. 8, а) згідно відомому значенню 5. За умовою 6. За частотою зрізу 7. Проводять сполучення середньочастотної частини БЛАХ з низькочастотною ділянкою ЛАХ нескорегованої САС. При цьому необхідно мати на увазі два наступні положення: а) якщо за ТВ визначені вимоги по точності і порядку астатизму, то сполучення слід починати з низькочастотної ділянки; б) якщо вимоги по точності не визначені ТВ, то сполучення слід починати з середньочастотної ділянки. 8. Проводять сполучення середньочастотної ділянки БЛАХ з високочастотною ділянкою нескорегованої САС з умови отримання простого виду корегуючої ланки, тобто нахил високочастотної ділянки БЛАХ вибирають рівним нахилу високочастотної ділянки нескорегованої САС. Нехай корегуючий пристрій, яким здійснюється корекція спроектованої САС, має передаточну функцію Якщо виразити передаточні функції нескорегованої і скорегованої САС відповідно через
Логарифмічна амплітудно-частотна характеристика матиме вигляд:
звідки можна знайти логарифмічну характеристику послідовного корегуючого пристрою:
Логарифмічна фазово-частотна характеристика визначиться за співвідношенням
Логарифмічна характеристика скорегованої САС Для спрощення процесу вибору корегуючого пристрою користуються таблицями типових КП (див. таблицю 2), де наведені їх характеристики та електричні схеми. Для вибору паралельної корегуючої ланки необхідно виконати таку послідовність операцій: 1. побудувати нескореговану ЛАХ за умовами фізичної реалізації; 2. побудувати БЛАХ, виходячи із заданих ТВ; 3. визначити ланку, або ланки, що підлягають обхвату зворотними зв’язками залежно від структурної схеми САС і рекомендацій про вплив різних зворотних зв’язків; 4. побудувати ЛАХ послідовної корегуючої ланки, віднявши з бажаної ЛАХ нескореговану; 5. побудувати ЛАХ ланки (ланок), що намічається для обхвату зворотним зв’язком; 6. побудувати ЛАХ паралельної корегуючої ланки шляхом складання ЛАХ ланок, що охоплюються зворотним зв’язком і ЛАХ послідовної корегуючої ланки, а потім отримати дзеркальне відображення сумарної ЛАХ. Отже, частотна передаточна функція скорегованої системи може бути представлена у вигляді:
де
Дискретні САС САС називається дискретною, якщо вона містить, хоча б одну ланку дискретної дії. Дискретна ланка – це ланка, вихідна величина якої змінюється дискретно, тобто стрибкоподібно, навіть при плавній зміні вхідної величини. Дискретний елемент перетворює безперервні сигнали в дискретні за рахунок квантування вхідних сигналів. Розрізняють три види квантування [12]: 1) квантування сигналу за рівнем (рис. 9, а) – фіксуються певні дискретні значення рівнів сигналу в довільні моменти часу. Системи з квантуванням сигналу за рівнем називаються релейними. Вони завжди «нелінійні». 2) квантування сигналу за часом (рис. 9, б) – значення сигналу, що безперервно змінюється, передаються дискретно через певні проміжки часу (у вигляді імпульсів). Безперервний сигнал представляється у вигляді послідовності короткочасних імпульсів, а між імпульсами квантований сигнал не фіксується. Системи з квантуванням сигналу за часом називаються імпульсними. Імпульсні системи можуть бути лінійними і нелінійними. 3) квантування сигналу за рівнем і за часом (рис. 9, в) – безперервний сигнал представляється у вигляді послідовності чисел, які передаються в дискретні моменти часу. При цьому безперервний сигнал замінюється дискретними рівнями, найближчими до значень безперервного сигналу в дискретні моменти часу. Квантування сигналів за рівнем і за часом здійснюється імпульсно-кодовим модулятором або цифровим обчислювальним пристроєм (ЦОП). Системи з квантуванням сигналів за часом і за рівнем називаються цифровими. Вони завжди нелінійні, але в деяких випадках в першому наближенні можуть розглядатися як лінійні імпульсні.
Імпульсні і цифрові САС дозволяють формувати закони управління з урахуванням зміни збурюючих дій і характеристик керованого об’єкту, тобто такі САС мають властивості самоналагоджувальних та оптимальних систем, систем із змінною структурою. Будь-яку імпульсну систему можна представити у вигляді з’єднання імпульсного елементу (ІЕ) і безперервної частини системи (БЧ). У замкнутій імпульсній системі імпульсний елемент знаходиться усередині замкнутого контуру; він може входити до складу прямого кола або кола зворотного зв’язку. Загальну функціональну схему імпульсної САС можна представити у вигляді, зображеному на рис. 10. Основна відмінність імпульсної САС від безперервної полягає в тому, що сигнал розузгодження в ній виробляється і подається на безперервну частину системи в дискретні моменти часу. У ці моменти відбувається замикання системи, в решті часу імпульсна система працює як розімкнена. Оскільки безперервна частина імпульсної або цифрової САС реагує на дії тільки в певні дискретні моменти часу (визначувані роботою імпульсного елементу або ЦОП), ці дії можна представити у вигляді функцій дискретного аргументу, тобто так званими ґратчастими функціями.
Решітчастою функцією називають таку функцію, значення якої фіксуються тільки при дискретних рівновіддалених (на період) один від одного значеннях аргументу, а між цими значеннями незалежної змінної функція дорівнює нулю. Решітчаста функція позначається символом Співвідношення між решітчастою функцією До різницевих рівнянь приводяться різні задачі, зокрема з теорії інтерполяції. ЦОП описується різницевими рівняннями, які визначають собою послідовність його дій і зазвичай називаються програмами. Для дослідження цифрових, а також імпульсних систем застосовують [12] апарат дискретного перетворення Лапласа. В даний час для аналізу і синтезу дискретних САС широко використовується так зване z-перетворення. Для будь-якої функції х(t), для якої можливе перетворення Лапласа можна знайти z-перетворення відповідно до формули:
У стійкій дискретній системі корені характеристичного рівняння повинні лежати усередині кола з одиничним радіусом (рис. 11), тобто Для оцінки якості роботи імпульсних і цифрових САС необхідно побудувати криву перехідного процесу, тобто визначити закон зміни вихідної величини
Для визначення кривої перехідного процесу потрібно отримати вираз дискретного перетворення Лапласа від вихідної величини II. ПРАКТИЧНА ЧАСТИНА.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , перерегулювання
, перерегулювання  %, запас стійкості за фазою
%, запас стійкості за фазою  , амплітуду Н, помилки в сталому режимі
, амплітуду Н, помилки в сталому режимі  і
і  .
. . На практиці низькочастотна ділянка
. На практиці низькочастотна ділянка  оцінюється приблизно за величиною:
оцінюється приблизно за величиною:  , де
, де  − інтервал частоти додатної дійсної частотної характеристики замкнутої системи
− інтервал частоти додатної дійсної частотної характеристики замкнутої системи  . У цьому діапазоні повинна бути виконане умова:
. У цьому діапазоні повинна бути виконане умова: ,
,
 − деяка задана величина, зазвичай приймають
− деяка задана величина, зазвичай приймають  .
. , запаси стійкості за фазою та амплітудою. Побудова середньочастотної ділянки логарифмічно-амплітудної характеристики (ЛАХ) полягає у визначенні частоти зрізу
, запаси стійкості за фазою та амплітудою. Побудова середньочастотної ділянки логарифмічно-амплітудної характеристики (ЛАХ) полягає у визначенні частоти зрізу  за заданими показниками якості і в проведенні на ділянці
за заданими показниками якості і в проведенні на ділянці  , дБ (рис. 7) логарифмічної характеристики з нахилом -20 дБ/дек. Інтервал середньочастотної ділянки
, дБ (рис. 7) логарифмічної характеристики з нахилом -20 дБ/дек. Інтервал середньочастотної ділянки  , що відповідає ординатам
, що відповідає ординатам  , визначається із співвідношень:
, визначається із співвідношень:  ,
,  . Значення коефіцієнта
. Значення коефіцієнта  може бути знайдено за графіком (рис. 8, в). На практиці значення
може бути знайдено за графіком (рис. 8, в). На практиці значення  та
та  складають ± 16 дБ при забезпеченні запасів стійкості
складають ± 16 дБ при забезпеченні запасів стійкості  ,
,  дБ. Середньочастотна ділянка зазвичай дорівнює інтервалу частот в одну декаду.
дБ. Середньочастотна ділянка зазвичай дорівнює інтервалу частот в одну декаду. визначає згладжуючі властивості системи по відношенню до перешкод. Чим більше нахил високочастотної ділянки ЛАХ, тим більше перешкодостійкість САС. На практиці зазвичай приймають
визначає згладжуючі властивості системи по відношенню до перешкод. Чим більше нахил високочастотної ділянки ЛАХ, тим більше перешкодостійкість САС. На практиці зазвичай приймають  .
. знаходять значення додатної частини дійсної частотної характеристики
знаходять значення додатної частини дійсної частотної характеристики  , при цьому від’ємну частину дійсної частотної характеристики
, при цьому від’ємну частину дійсної частотної характеристики 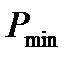 визначають за виразом:
визначають за виразом: 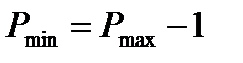 .
. і фазою
і фазою 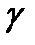 .
.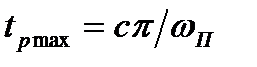 .Згідно заданому за ТВ значенню
.Згідно заданому за ТВ значенню  знаходять
знаходять  − інтервал частоти позитивності дійсної частотної характеристики замкнутої системи.
− інтервал частоти позитивності дійсної частотної характеристики замкнутої системи. вибирають частоту зрізу
вибирають частоту зрізу  .
.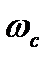 будують середньочастотну частину БЛАХ з нахилом -20 дБ/дек.
будують середньочастотну частину БЛАХ з нахилом -20 дБ/дек. .
. і
і  , то при послідовному з’єднанні нескорегованої САС і корегуючого пристрою, дотримується умова:
, то при послідовному з’єднанні нескорегованої САС і корегуючого пристрою, дотримується умова: .
.
 ,
,
 .
.
 .
.
 є бажаною ЛАХ. Логарифмічна характеристика нескорегованої САС є ЛАХ спроектованої системи з умов її фізичної реалізації. Таким чином, логарифмічна характеристика послідовного корегуючого пристрою, може бути отримана в результаті віднімання від бажаної ЛАХ логарифмічної характеристики спроектованої реальної САС.
є бажаною ЛАХ. Логарифмічна характеристика нескорегованої САС є ЛАХ спроектованої системи з умов її фізичної реалізації. Таким чином, логарифмічна характеристика послідовного корегуючого пристрою, може бути отримана в результаті віднімання від бажаної ЛАХ логарифмічної характеристики спроектованої реальної САС. ,
,
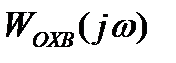 − передаточна функція послідовності ланок, охоплених зворотним зв’язком;
− передаточна функція послідовності ланок, охоплених зворотним зв’язком;  − передаточна функція зворотного зв’язку.
− передаточна функція зворотного зв’язку. , де
, де  − додатна величина, що визначає відстань між сусідніми дискретними значеннями незалежної змінної t, а п – будь-яке ціле число (n = 0, 1, 2...).
− додатна величина, що визначає відстань між сусідніми дискретними значеннями незалежної змінної t, а п – будь-яке ціле число (n = 0, 1, 2...).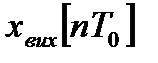 і її різницями різних порядків
і її різницями різних порядків  визначає рівняння, зване різницевим рівнянням. Різницеві рівняння з’являються при дослідженні фізичних систем, в яких частина змінних змінюється дискретно або стрибкоподібно. Наприклад, в ланцюгових схемах електроустаткування суден (фільтри, еквіваленти довгих ліній, гірлянди ізоляторів, дільники напруги тощо). У колах з параметрами, що стрибкоподібно змінюються, такою змінною є час.
визначає рівняння, зване різницевим рівнянням. Різницеві рівняння з’являються при дослідженні фізичних систем, в яких частина змінних змінюється дискретно або стрибкоподібно. Наприклад, в ланцюгових схемах електроустаткування суден (фільтри, еквіваленти довгих ліній, гірлянди ізоляторів, дільники напруги тощо). У колах з параметрами, що стрибкоподібно змінюються, такою змінною є час. .
.
 .
. при відомих структурі і параметрах системи.
при відомих структурі і параметрах системи. . Якщо відома
. Якщо відома  , то, розклавши її на прості дроби і застосувавши зворотне перетворення Лапласа (для чого можна використовувати таблицю відповідностей), неважко визначити криву перехідного процесу.
, то, розклавши її на прості дроби і застосувавши зворотне перетворення Лапласа (для чого можна використовувати таблицю відповідностей), неважко визначити криву перехідного процесу.


