
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перелік скорочень та умовних позначеньСодержание книги
Поиск на нашем сайте
ПЕРЕЛІК СКОРОЧЕНЬ ТА УМОВНИХ ПОЗНАЧЕНЬ 1. АЧХ – амплітудно-частотна характеристика; 2. БЛАХ – бажана логарифмічно-амплітудна характеристика; 3. БЛАЧХ – бажана логарифмічно-амплітудно-частотна характеристика; 4. БЧ – безперервна частина системи; 5. ГЗЗ – гнучкий зворотній зв’язок; 6. ЕОМ – електронна обчислювальна машина; 7. ЖЗЗ – жорсткий зворотній зв’язок; 8. ІЕ – імпульсний елемент; 9. КП – корегуючий пристрій; 10. ЛАХ – логарифмічно-амплітудна характеристика; 11. ЛАЧХ – логарифмічно-амплітудно-частотна характеристика; 12. ОУ – об’єкт управління; 13. ПЗ – пояснювальна записка; 14. ПУ – пристрій управління; 15. САС – суднові автоматичні системи; 16. САУ – система автоматичного управління; 17. ТВ – технічні вимоги; 18. ФЧХ – фазо-частотна характеристика; 19. ЦОМ – цифрова обчислювальна машина; 20. ЦОП – цифровий обчислювальний пристрій. ЗАВДАННЯ НА КУРСОВУ РОБОТУ Тема курсової роботи: «Розрахунок суднової динамічної системи автоматичного управління із заданими показниками якості» Завдання на курсову роботу містить у собі наступні складники: 1. Відповідно до варіанту задана певна електромеханічна система судна. Необхідно: 1) за наведеною структурною схемою системи і заданими передаточними функціями кожного елементу (блоку) системи розрахувати корегуючий пристрій, при якому перехідний процес задовольняв би заданим показникам якості (час регулювання і перерегулювання); 2) провести синтез дискретної системи управління, а саме: реалізувати розрахований корегуючий пристрій на цифровій обчислювальній машині (ЦОМ). 2. Пояснювальна записка має включати наступні розділи: 1) Вступ. 2) Приведення структурної схеми до стандартного вигляду. 3) Побудова логарифмічно-амплітудно-частотної характеристики (ЛАЧХ) початкової системи, бажаної системи та корегуючого пристрою. 4) Технічна реалізація аналогового корегуючого пристрою. 5) Побудова перехідної характеристики скорегованої системи. 6) Отримання дискретної передаточної функції цифрової системи. 7) Побудова перехідної характеристики дискретної системи. 8) Реалізація передаточної функції і алгоритму роботи електронної обчислювальної машини (ЕОМ) – як дискретного корегуючого пристрою. 9) Висновок. 3. Оформлення пояснювальної записки і креслень згідно ДСТУ 3008-95 [6].
ВСТУП У системі підготовки бакалаврів суднової електромеханіки важливе місце займає оволодіння фундаментальними основами теорії автоматичного управління стосовно суднових автоматизованих комплексів. Спеціальна підготовка бакалавра суднової електромеханіки, починаючи від вивчення суднових систем електроенергетики і закінчуючи питаннями комплексної автоматизації суден, базується на основоположних питаннях побудови, аналізу і синтезу суднових лінійних, нелінійних і дискретних систем, а також на знаннях про особливості побудови і аналізу адаптивних і оптимальних автоматичних систем. Управління [10] складає невід’ємну частину незліченних процесів, що відбуваються в живій і неживій природі. Найбільш загальним вченням про керовані процеси в природі є кібернетика, яка вивчає методи цілеспрямованого управління будь-якими складними динамічними системами, використовуючи спільність процесів управління в живих організмах і автоматах. Область науки і техніки, що охоплює теорію і принципи побудови систем управління технічними процесами, що діють без участі людини, називається автоматикою. Широке та інтенсивне освоєння Світового океану зумовило будівництво різноманітних надводних і підводних суден, що постійно росте. Розвиток суднової автоматики пов’язаний з успіхами сучасного суднобудування, підвищенням енергоозброєності та ускладненням систем електроустаткування суден, впровадженням на суднах атомних установок. Вдосконалення технічних показників суден немислиме без широкого використання автоматизації і автоматичного управління, без застосування різноманітних засобів автоматики. Розвиток суднової автоматики відбувався в тісному зв’язку із загальним розвитком теорії автоматичного управління. Від виникнення простих автоматів до сучасних складних автоматичних систем управління пройдено великий шлях, який можна розбити на два нерівних по тривалості періоду. Перший період охоплює багатотисячолітній етап «неусвідомленої» автоматики, пов’язаний з винаходом різних по складності і призначенню оригінальних автоматів і автоматичних пристроїв. Другий період налічує більш ніж 100 років з часу початку розробки наукових основ створення автоматичних систем, що задовольняють певним заданим вимогам якості. Основними завданнями теорії автоматичного управління є дослідження статичних і динамічних властивостей автоматичних систем і розробка систем, що задовольняють заданим технічним вимогам. Завдання аналізу і синтезу в даний час в значній мірі вирішені стосовно лінійних систем, що задовольняють принципу суперпозиції. Оволодіння навичками аналізу і синтезу лінійних систем є основою при вивченні курсу теорії автоматичного управління. Важливе місце, з інженерної точки зору, займають частотні методи дослідження лінійних систем, що розкривають фізичну суть процесів управління. З іншого боку, поява і швидке вдосконалення мікропроцесорних засобів зумовили доцільність їх застосування в системах управління. Завдання, які доводиться вирішувати ЦОМ в системах управління, дуже різноманітні, серед них одним з найбільш важливих є забезпечення бажаних динамічних характеристик за допомогою створення корегуючих програм в ЦОМ. В даних методичних вказівках перша частина курсової роботи з теорії автоматичного управління охоплює теорію безперервних автоматичних систем управління, а друга частина присвячена теорії дискретних систем управління. Виконання курсової роботи передбачає використання програми Mathcad, а також пакету Simulink системи matlab, які є стандартним інструментом для роботи в різних областях математики, машинобудування і науки. matlab – це високопродуктивна мова для технічних розрахунків, що включає обчислення, візуалізацію і програмування в зручному середовищі, де завдання і розв’язки виражаються у формі, близькій до математичної.
I. ТЕОРЕТИЧНА ЧАСТИНА При управлінні яким-небудь процесом вручну людина-оператор здійснює наступні функції: 1) стежить за ходом процесу, спостерігаючи за допомогою вимірювальних приладів або безпосередньо за зміною параметра, що характеризує його (або ряду параметрів); 2) порівнюючи дійсне значення цього параметра з його заданим значенням, визначає величину і знак відхилення; 3) відповідно до відхилення, що утворилося, за допомогою якого-небудь пристрою впливає на процес так, щоб усунути це відхилення. Управління, здійснюване без участі людини, називається автоматичним управлінням.
Стійкість САС Для того, щоб суднові автоматичні системи виконували своє призначення, вони повинні бути, перш за все, стійкими. Система вважається стійкою, якщо відхилення вихідної величини, що виникає в результаті зовнішнього збурення, після закінчення деякого часу стає менше заданого значення. Отже, система, виведена із сталого стану, а потім надана самій собі, повинна повернутися в стан рівноваги. Якщо ж система після дії збурення не приходить в сталий стан, а здійснює коливання з постійною або зростаючою амплітудою, вона називається нестійкою. Аналіз на стійкість – одне з основних завдань теорії автоматичного управління. Вперше загальне визначення стійкості було дане російським математиком А. М. Ляпуновим. На підставі теорем Ляпунова були сформульовані умови стійкості лінійних і нелінійних систем, що отримали назви першого і другого методів Ляпунова і що дозволяють досліджувати стійкість широкого класу динамічних систем. Про стійкість лінійних САС міркують по збіжності процесу управління після припинення зовнішніх дій, тобто по характеру власного руху системи. Отже, про стійкість САС можна міркувати на основі розв’язання характеристичного рівнянні замкнутої САС:
за видом його коренів або розташуванню полюсів САС на комплексній площині. САС буде стійкою, якщо всі дійсні корені характеристичного рівняння і всі дійсні частини комплексно-зв’язаного коріння від’ємні. Іншими словами, САС є стійкою, якщо передаточна функція замкнутої системи Дослідження поведінки САС в перехідному режимі, пов’язане з розв’язанням характеристичного рівняння і аналізом характеру його коріння, виконується порівняно легко лише в простих випадках, тобто при розв’язанні рівнянь другого або третього порядку. Розв’язання характеристичного рівняння вищих ступенів – складний і трудомісткий процес. Тому були знайдені методи, що дозволяють без обчислення коренів характеристичного рівняння САС міркувати про її стійкість.
Такі непрямі показники стійкості САС отримали назву критеріїв стійкості, які можуть бути розділені на аналітичні (критерій Вишнєградського, критерій Гурвица тощо) і частотні (критерій Михайлова, амплітудно-фазовий критерій, критерій D - розбиття). Якісні показники САС Основним завданням при проектуванні є створення САС, що не тільки задовольняють умовам стійкості, але і відповідають певним технічним вимогам. Дослідження САС з погляду якісних характеристик переслідує мету такого вибору схеми або значень окремих параметрів САС, щоб вона задовольняла поставленим технічним умовам. При розробці будь-якої САУ виходять з виконання двох загальних умов: фізичної реалізації системи, що забезпечує відробіток вихідної величини та забезпечення заданих технічних вимог. Якість САС повинна указувати, наскільки успішно справляється система з діями, що збурюють, і наскільки точно вона відтворює управляючі вхідні сигнали. Поняття про якість складається з окремих показників, які є характеристиками реакції системи на типові збурення. Реакція системи на одиничну ступінчасту дію за нульових початкових умов називається перехідною функцією системи 1) час регулювання 2) перерегулювання 3) число коливань Вважається, що система має необхідну якість, якщо показники якості не перевищують заданих значень, визначених призначенням системи (завданням). Перехідна функція
Крім того, перехідні функції (перехідні характеристики) САС можуть бути визначені при вирішенні диференціального рівняння, що описує динаміку системи або за допомогою моделювання САС на цифровій або аналоговій обчислювальній машині. Разом з прямими методами визначення перехідної функції розроблені непрямі методи оцінки (критерії) якості, що дозволяють порівняно просто без розв’язання рівняння системи приблизно міркувати про показники якості систем. До основних непрямих методів відносяться: частотний та інтегральний методи, засновані на вивченні розподілу нулів і полюсів передаточної функції системи. Визначення основних показників якості Перехідний процес дає уявлення про те, за яким законом і як скоро вихідна величина набуває нових значень, що задається дією на вхід САС.
Часом встановлення, або часом регулювання
стане менше заданого значення Перерегулювання
Іншими словами, перерегулювання За показник якості САС може бути прийняте число коливань Крім того, до реальних САС пред’являються вимоги точності, швидкодії і забезпечення захисту від перешкод (смуги пропускання). У сталому режимі точність суднових автоматичних систем визначається: − статичною помилкою − швидкісною помилкою − помилкою, пропорційною прискоренню З вимогою точності САС безпосередньо пов’язано забезпечення смуги пропускання частот Швидкодія характеризується швидкістю наростання перехідного процесу за час
З швидкодією САС пов’язана одна з її важливих характеристик, звана добротністю. Добротність САС визначається відношенням загального коефіцієнта підсилення до постійної часу системи:
При проектуванні лінійних САС необхідно добиватися оптимального співвідношення між швидкодією, точністю і перешкодостійкістю. У теорії САС використовують аналітичні методи непрямих оцінок якості перехідного процесу. Так для оцінки швидкодії перехідного процесу може бути використане поняття «Ступені стійкості». Відомо, що САС стійка, якщо її полюси розташовуються в комплексній площині зліва від уявної осі. Якість перехідного процесу визначатиметься часом регулювання Швидкість загасання перехідного процесу визначається коренем, найменшим по абсолютній величині дійсної частини. Відповідно до цих міркувань, ступенем стійкості
Поставимо вимогу, щоб час перехідного процесу не перевищував
Якщо найближчими до уявної осі є комплексно-зв’язані коріння вигляду
В цьому випадку
Якщо час регулювання, визначений за вищенаведеними виразами, буде рівний або менший заданого часу регулювання У разі коливального перехідного процесу для оцінки якості САС важливо оцінити коливальність системи. Мірою коливальності є відношення уявної частини кореня, що характеризує кутову частоту коливань, до дійсної частини у вигляді:
Крім того, дійсна і уявна частини кореня характеристичного рівняння визначають період Значення ступеня коливальності
Окрім описаного алгебраїчного методу оцінки якості САС, існують інтегральний, частотний методи, метод трапецеїдальних характеристик. Застосування того або іншого методу визначається наявними засобами оцінки якості САС.
Корегуючі пристрої Корегуючі пристрої (КП) – це пристрої, які вводять в САС для поліпшення якості управління, для зміни (корекції) її характеристик. До корегуючих пристроїв, призначених для поліпшення динамічних властивостей САС, відносяться елементи, що характеризуються передаточними функціями диференціюючих ланок. Вибір і розрахунок систем корекції складає головний зміст динамічного розрахунку САС. Він здійснюється методом аналізу або синтезу. Вибір КП методом аналізу зводиться до послідовного поліпшення динамічних властивостей системи. Вибір КП методом синтезу здійснюється безпосередньо з умов отримання необхідного перехідного процесу. На практиці методи аналізу і синтезу органічно доповнюють один одного. Введення в закон управління сигналів, пропорційних похідним, дозволяє забезпечити необхідні якості САС (потрібні швидкодія і запаси стійкості) як в перехідному (динамічному), так і в сталому режимі, а також додати системі стабілізуючі властивості. Введенням в закон управління інтегралів досягається необхідний порядок астатизму з метою забезпечення у системі необхідних величин помилок Корегуючі пристрої в коло одноконтурної САС можуть бути включені послідовно або паралельно. При введенні послідовних корегуючих кіл в САС необхідно оцінювати їх позитивні і негативні сторони. Введення таких кіл є зручним, зважаючи на простоту і наочність формування управляючих дій, а, отже, порівняльної простоти їх вибору і розрахунку. Це пояснюється тим, що послідовні корегуючі кола вводяться в прямий тракт підсилення і перетворення управляючого сигналу і там, де це виявляється можливим за умовами фільтрації сигналу від перешкод, вони з успіхом виконують своє завдання. Паралельні корегуючі кола застосовують тоді, коли потрібно здійснити складний закон управління з введенням похідних і інтегралів від сигналу помилки. Паралельне включення інтегруючих і диференціюючих корегуючих кіл дозволяє підвищити точність роботи каналу управління без значного зниження його запасу стійкості. Для введення в закон управління сигналів, пропорційних похідним та інтегралам, застосовують різні за конструктивним виконанням і фізичними основами пристрої. Корегуючі пристрої, діляться на активні і пасивні. До активних відносяться диференціюючі та інтегруючі гіроскопи, гіротахоакселерометри, операційні підсилювачі, тахогенератори, сервомотори, до пасивних – різного роду пасивні чотириполюсники, звані в теорії САС корегуючими колами. Пристрої пасивного типу не містять джерел енергії, потужність вихідного сигналу у них менша, ніж потужність вхідного. У САС найбільш широке застосування отримали корегуючі пристрої у вигляді пасивних кіл, що складаються з різних з’єднань активних опорів На практиці для корекції САС використовують різноманітні схеми пасивних корегуючих кіл; деякі з них наведено в таблиці 2. Для зміни властивостей ланки або сукупності ланок в системах управління разом з послідовними і паралельними корегуючими пристроями широко застосовуються зустрічно-паралельні корегуючі кола у вигляді різного роду місцевих зворотних зв’язків, а також їх комбінації [12].
Таблиця 2 – Основні схеми пасивних корегуючих кіл
Перетворення динамічних властивостей ланки або кола ланок при обхваті зворотним зв’язком проводиться відповідно до формули:
де При жорсткому зворотному зв’язку сигнал з виходу охоплюваної ланки (кола ланок) діє постійно (жорстко) як в перехідному, так і в сталому режимі. При гнучкому зворотному зв'язку сигнал з виходу охоплюваної ланки (кола ланок) діє вибірково (гнучко) в перехідному і сталому режимах. Зазвичай в якості ГЗЗ використовують диференціюючі та інтегруючі кола. Для корекції в системах управління застосовують переважно від’ємні зворотні зв’язки. Додатні зворотні зв’язки використовують лише в елементах САС для збільшення коефіцієнта підсилення або зменшення постійної часу (наприклад, в магнітному підсилювачі).
Дискретні САС САС називається дискретною, якщо вона містить, хоча б одну ланку дискретної дії. Дискретна ланка – це ланка, вихідна величина якої змінюється дискретно, тобто стрибкоподібно, навіть при плавній зміні вхідної величини. Дискретний елемент перетворює безперервні сигнали в дискретні за рахунок квантування вхідних сигналів. Розрізняють три види квантування [12]: 1) квантування сигналу за рівнем (рис. 9, а) – фіксуються певні дискретні значення рівнів сигналу в довільні моменти часу. Системи з квантуванням сигналу за рівнем називаються релейними. Вони завжди «нелінійні». 2) квантування сигналу за часом (рис. 9, б) – значення сигналу, що безперервно змінюється, передаються дискретно через певні проміжки часу (у вигляді імпульсів). Безперервний сигнал представляється у вигляді послідовності короткочасних імпульсів, а між імпульсами квантований сигнал не фіксується. Системи з квантуванням сигналу за часом називаються імпульсними. Імпульсні системи можуть бути лінійними і нелінійними. 3) квантування сигналу за рівнем і за часом (рис. 9, в) – безперервний сигнал представляється у вигляді послідовності чисел, які передаються в дискретні моменти часу. При цьому безперервний сигнал замінюється дискретними рівнями, найближчими до значень безперервного сигналу в дискретні моменти часу. Квантування сигналів за рівнем і за часом здійснюється імпульсно-кодовим модулятором або цифровим обчислювальним пристроєм (ЦОП). Системи з квантуванням сигналів за часом і за рівнем називаються цифровими. Вони завжди нелінійні, але в деяких випадках в першому наближенні можуть розглядатися як лінійні імпульсні.
Імпульсні і цифрові САС дозволяють формувати закони управління з урахуванням зміни збурюючих дій і характеристик керованого об’єкту, тобто такі САС мають властивості самоналагоджувальних та оптимальних систем, систем із змінною структурою. Будь-яку імпульсну систему можна представити у вигляді з’єднання імпульсного елементу (ІЕ) і безперервної частини системи (БЧ). У замкнутій імпульсній системі імпульсний елемент знаходиться усередині замкнутого контуру; він може входити до складу прямого кола або кола зворотного зв’язку. Загальну функціональну схему імпульсної САС можна представити у вигляді, зображеному на рис. 10. Основна відмінність імпульсної САС від безперервної полягає в тому, що сигнал розузгодження в ній виробляється і подається на безперервну частину системи в дискретні моменти часу. У ці моменти відбувається замикання системи, в решті часу імпульсна система працює як розімкнена. Оскільки безперервна частина імпульсної або цифрової САС реагує на дії тільки в певні дискретні моменти часу (визначувані роботою імпульсного елементу або ЦОП), ці дії можна представити у вигляді функцій дискретного аргументу, тобто так званими ґратчастими функціями.
Решітчастою функцією називають таку функцію, значення якої фіксуються тільки при дискретних рівновіддалених (на період) один від одного значеннях аргументу, а між цими значеннями незалежної змінної функція дорівнює нулю. Решітчаста функція позначається символом Співвідношення між решітчастою функцією До різницевих рівнянь приводяться різні задачі, зокрема з теорії інтерполяції. ЦОП описується різницевими рівняннями, які визначають собою послідовність його дій і зазвичай називаються програмами. Для дослідження цифрових, а також імпульсних систем застосовують [12] апарат дискретного перетворення Лапласа. В даний час для аналізу і синтезу дискретних САС широко використовується так зване z-перетворення. Для будь-якої функції х(t), для якої можливе перетворення Лапласа можна знайти z-перетворення відповідно до формули:
У стійкій дискретній системі корені характеристичного рівняння повинні лежати усередині кола з одиничним радіусом (рис. 11), тобто Для оцінки якості роботи імпульсних і цифрових САС необхідно побудувати криву перехідного процесу, тобто визначити закон зміни вихідної величини
Для визначення кривої перехідного процесу потрібно отримати вираз дискретного перетворення Лапласа від вихідної величини II. ПРАКТИЧНА ЧАСТИНА. Синтез дискретної системи Завдання ЦОМ [12] (цифрової обчислювальної машини) полягає в забезпеченні бажаних динамічних характеристик системи управління за допомогою використання в ЦОМ програм, що коректують. У цьому випадку ЦОМ є по суті цифровий фільтр із заданими характеристиками. Цифрові системи управління мають квантування за часом, що відносить їх до класу дискретних (імпульсних) систем, і квантування за рівнем (у аналого-цифрових і цифро-аналогових перетворювачах). Якщо розрядність вхідних і вихідних перетворювачів достатньо велика, то їх нелінійністю можна нехтувати, при цьому розглядається лінеаризована дискретна система з урахуванням впливу, що надається квантуванням за рівнем, у вигляді додаткового шуму квантування, що розглядається як випадковий процес з рівноімовірним законом розпо
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.156.226 (0.015 с.) |

 ,
,
 не матиме полюсів в правій напівплощині. Уявна вісь
не матиме полюсів в правій напівплощині. Уявна вісь  є межею стійкості на комплексній площині. При цьому заштрихована ліва напівплощина полюсів відповідає стійкій САС (рис. 4).
є межею стійкості на комплексній площині. При цьому заштрихована ліва напівплощина полюсів відповідає стійкій САС (рис. 4). яка оцінюється за допомогою сукупності характеристик, званих показниками якості перехідного процесу системи. Ними є:
яка оцінюється за допомогою сукупності характеристик, званих показниками якості перехідного процесу системи. Ними є: ;
; ;
; .
. , знаходиться по її зображенню за допомогою зворотного перетворення Лапласа:
, знаходиться по її зображенню за допомогою зворотного перетворення Лапласа: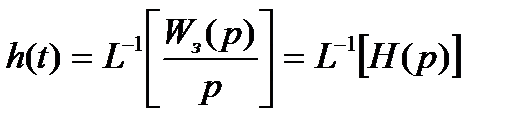 .
.
 на типових перехідних процесах наведено на рис. 5.
на типових перехідних процесах наведено на рис. 5.
 . Зазвичай
. Зазвичай  стає і надалі залишається меншим допустимого значення
стає і надалі залишається меншим допустимого значення  для лінійних систем визначається у відсотках по формулі:
для лінійних систем визначається у відсотках по формулі: .
.
 (число викидів) вихідної величини
(число викидів) вихідної величини  протягом часу перехідного процесу
протягом часу перехідного процесу  або статизмом
або статизмом 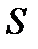 (для статичних систем);
(для статичних систем); (для астатичних систем першого порядку);
(для астатичних систем першого порядку); (для астатичних систем другого порядку).
(для астатичних систем другого порядку). , при якій відбувається точний відробіток управляючої дії та обмеження збурюючої дії.
, при якій відбувається точний відробіток управляючої дії та обмеження збурюючої дії. зміни перехідної характеристики від 10 до 90 %сталого значення. Залежність швидкодії
зміни перехідної характеристики від 10 до 90 %сталого значення. Залежність швидкодії 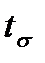 і частоти зрізу
і частоти зрізу  (або смуги пропускання
(або смуги пропускання  .
.
 .
.
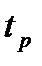 , яке залежить від абсолютних значень дійсних частин коренів характеристичного рівняння системи.
, яке залежить від абсолютних значень дійсних частин коренів характеристичного рівняння системи. називають відстань від уявної осі до найближчого дійсного кореня або дійсної частини пари комплексно-зв’язаних коренів характеристичного рівняння (рис. 6). Якщо найближчим до уявної осі є дійсний корінь, то складова в перехідному процесі, визначувана цим коренем, представлятиме затухаючу експоненту
називають відстань від уявної осі до найближчого дійсного кореня або дійсної частини пари комплексно-зв’язаних коренів характеристичного рівняння (рис. 6). Якщо найближчим до уявної осі є дійсний корінь, то складова в перехідному процесі, визначувана цим коренем, представлятиме затухаючу експоненту 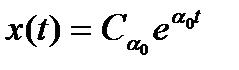 . При цьому
. При цьому  . Тоді величина
. Тоді величина  .
.
 , то складова, визначувана цими коріннями, матиме вид затухаючого коливального процесу:
, то складова, визначувана цими коріннями, матиме вид затухаючого коливального процесу: .
.
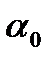 називається коливальним ступенем стійкості. Для спрощення, припустивши, що
називається коливальним ступенем стійкості. Для спрощення, припустивши, що  , верхня межа часу перехідного процесу у вигляді нерівності може бути знайдена як:
, верхня межа часу перехідного процесу у вигляді нерівності може бути знайдена як: .
.
 за технічними вимогами
за технічними вимогами  , то дійсний час регулювання досліджуваної системи задовольнятиме вимогам якості.
, то дійсний час регулювання досліджуваної системи задовольнятиме вимогам якості. .
.
 і частоту коливань
і частоту коливань  перехідного процесу.
перехідного процесу. дозволяє знайти наближене значення перерегулювання перехідної характеристики з виразу:
дозволяє знайти наближене значення перерегулювання перехідної характеристики з виразу: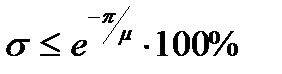 .
.
 і
і  .
. , ємностей С, індуктивностей
, ємностей С, індуктивностей  (кіл
(кіл  або
або  ). Пасивними корегуючими колами є чотириполюсники, вихідна напруга яких з певною точністю пропорційна похідній (похідним) або інтегралу від вхідної напруги. Пасивні корегуючі кола можуть працювати на постійному і змінному струмі. Це важливо, оскільки рід струму істотним чином впливає на точність роботи, технічну реалізацію пристроїв, на вигляд характеристик. Найбільшого поширення в схемах САС набули корегуючі кола постійного струму завдяки їх великій точності і стійкості.
). Пасивними корегуючими колами є чотириполюсники, вихідна напруга яких з певною точністю пропорційна похідній (похідним) або інтегралу від вхідної напруги. Пасивні корегуючі кола можуть працювати на постійному і змінному струмі. Це важливо, оскільки рід струму істотним чином впливає на точність роботи, технічну реалізацію пристроїв, на вигляд характеристик. Найбільшого поширення в схемах САС набули корегуючі кола постійного струму завдяки їх великій точності і стійкості. ;
;
 ;
;
 ;
;
 ;
;
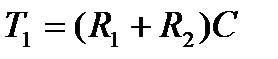 ;
;  .
.
 ;
;
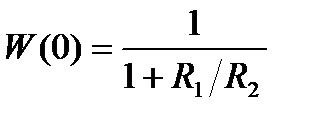 ;
;
 ;
;
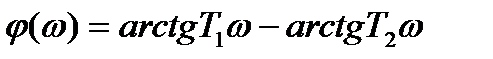 ;
;
 ;
;  .
.

 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
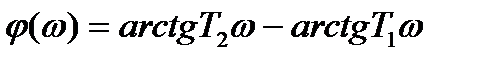 ;
;
 ;
;  .
.

 ;
;
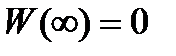 ;
;
 ;
;  .
.

 ;
;
 ,
,
 − передаточна функція ланки зворотного зв’язку. Залежно від виду передаточної функції
− передаточна функція ланки зворотного зв’язку. Залежно від виду передаточної функції  зворотні зв’язки діляться на жорсткі (ЖЗЗ) і гнучкі (ГЗЗ). Прикладом використання жорсткого і гнучкого зворотних зв’язків може служити слідкуюча система управління кермом з електромеханічним приводом.
зворотні зв’язки діляться на жорсткі (ЖЗЗ) і гнучкі (ГЗЗ). Прикладом використання жорсткого і гнучкого зворотних зв’язків може служити слідкуюча система управління кермом з електромеханічним приводом. , де
, де  − додатна величина, що визначає відстань між сусідніми дискретними значеннями незалежної змінної t, а п – будь-яке ціле число (n = 0, 1, 2...).
− додатна величина, що визначає відстань між сусідніми дискретними значеннями незалежної змінної t, а п – будь-яке ціле число (n = 0, 1, 2...).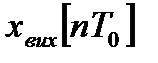 і її різницями різних порядків
і її різницями різних порядків  визначає рівняння, зване різницевим рівнянням. Різницеві рівняння з’являються при дослідженні фізичних систем, в яких частина змінних змінюється дискретно або стрибкоподібно. Наприклад, в ланцюгових схемах електроустаткування суден (фільтри, еквіваленти довгих ліній, гірлянди ізоляторів, дільники напруги тощо). У колах з параметрами, що стрибкоподібно змінюються, такою змінною є час.
визначає рівняння, зване різницевим рівнянням. Різницеві рівняння з’являються при дослідженні фізичних систем, в яких частина змінних змінюється дискретно або стрибкоподібно. Наприклад, в ланцюгових схемах електроустаткування суден (фільтри, еквіваленти довгих ліній, гірлянди ізоляторів, дільники напруги тощо). У колах з параметрами, що стрибкоподібно змінюються, такою змінною є час. .
.
 .
. при відомих структурі і параметрах системи.
при відомих структурі і параметрах системи. . Якщо відома
. Якщо відома  , то, розклавши її на прості дроби і застосувавши зворотне перетворення Лапласа (для чого можна використовувати таблицю відповідностей), неважко визначити криву перехідного процесу.
, то, розклавши її на прості дроби і застосувавши зворотне перетворення Лапласа (для чого можна використовувати таблицю відповідностей), неважко визначити криву перехідного процесу.


