Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем уравнений. Решение нелинейных уравненийСодержание книги
Поиск на нашем сайте Решение систем линейных уравнений. Рассмотрим методы решения системы линейных уравнений:
Прямые методы Правило Крамера. Одним из способов решения системы линейных уравнений является правило Крамера, согласно которому каждое неизвестное представляется в виде отношения определителей:
где D - определитель системы (1), Di – определители, полученные путем замены i-го столбца столбцом свободных членов системы (1). Правило обратной матрицы. Известен также метод решения линейной системы с использованием обратной матрицы. Система записывается в матричном виде А * Х = В. Тогда, умножая обе части этого уравнения слева на обратную матрицу А -1, получаем Х = А-1 * В. Метод Гаусса. Наиболее распространенными среди прямых методов являются метод исключения Гаусса и его модификации. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x2 из всех последующих уравнений системы. Затем с помощью второго уравнения исключается x 3 из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным xn, т.е. матрица системы будет приведена к треугольному виду. Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное xn. Далее, используя это значение, из предыдущего уравнения вычисляем xn -1 и т.д. Последним найдем x1 из первого уравнения. Примеры решения систем линейных алгебраических уравнений прямыми методами даны в приложении А.
Итерационные методы Метод простой итерации. При решении итерационными методами каждая переменная системы находится как предел последовательности приближений. Систему линейных уравнений записывают в виде:
Далее выбирают начальные приближения значений переменных x1(0 ), x2(0),…, xn(0 ) (любые n чисел) и подставляя их в правую часть системы, находят следующие приближенные значения корней x1(1), x2(1),…, xn(1) и т.д. Итерационный процесс продолжается до тех пор, пока не выполнится условие:
Условие сходимости итерационного процесса:
Для решения систем линейных уравнений в системе MathCad существуют встроенные функции: augment(A,B) – формирует расширенную матрицу системы, в первых столбцах которой содержится матрица А, а в последних – матрица В; rref(A) – выполняет прямой и обратный ход метода Гаусса; submatrix(A,i,j,l,m) – формирует столбец решения системы (то есть формирует матрицу, которая является блоком матрицы А, расположенны в строках с i по j в столбцах с l по m). В системе MathСad также реализовано решение систем линейных и нелинейных уравнений итерационными методами. Для этого используются функции Given и Find (Приложение Б).
Задание 2.1. Исследуйте систему линейных уравнений и, если решение существует, найдите его по формулам Крамера. Вариант 1 1)
Вариант 2 1)
Вариант 3 1) Вариант 4 1)
Вариант 5 1)
Вариант 6 1)
Вариант 7 1)
Вариант 8 1)
Вариант 9 1) Вариант 10 1)
Вариант 11 1)
Вариант 12 1) Порядок выполнения задания: 1. Установите режим автоматического выполнения вычислений. 2. Введите матрицу системы. 3. Вычислите определитель матрицы системы. Система имеет единственное решение, если определитель отличен от нуля. 4. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей. 5. Найдите решение системы по формулам Крамера (2).
Задание 2.2. Решить систему уравнений задания 2.1 с помощью обратной матрицы. Порядок выполнения задания: 1. Введите матрицу системы и вектор-столбец правых частей. 2. Вычислите решение системы по формуле Х=А-1·В. 3. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.3. Решитьсистемулинейных уравнений задания 2.1 методом Гаусса.. Порядок выполнения задания: 1. Присвойте переменной ORIGIN значение, равное единице. 2. Введите матрицу системы и столбец правых частей. 3. Сформируйте расширенную матрицу системы. 4. Приведите расширенную матрицу системы к ступенчатому виду. 5. Сформируйте столбец решения системы. 6. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.4. Решить систему уравнений задания 2.1 с помощью встроенных функций Given и Find. Порядок выполнения задания: 1. Записать служебное слово Given. 2. Ввести систему уравнений. 3. Вывести решение с помощью функции Find.
Задание 2.5. Решитьсистемулинейных уравнений методом простых итераций.
Вариант 1 A =
Вариант 2 A = Вариант 3 A = Вариант 4 A = Вариант 5 A = Вариант 6 A = Вариант 7 A = Вариант 8 A = Вариант 9 A =
Вариант 10 A = Вариант 11 A = Вариант 12 A =
Порядок выполнения задания: 1. Преобразуйте исходную систему Сх=d к виду х=B+Ах. 2. Проверьте достаточное условие сходимости. 3. Введите матрицы А и B. 4. Определите нулевое (начальное) приближение решения. 5. Задайте количество итераций. 6. Введите формулу вычисления последовательных приближений решения и вычислите их. 7. Выведите на экран матрицу приближенных решений.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.005 с.) |

 (1)
(1)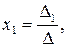
 …,
…,  , (2)
, (2)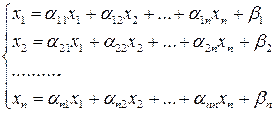 (3)
(3) k = 1,…,n
k = 1,…,n (4)
(4) 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 
 2)
2) 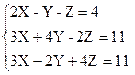
 2)
2) 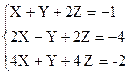
 2)
2) 
 2)
2) 
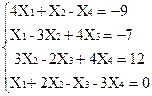 2)
2) 
 2)
2) 
 2)
2) 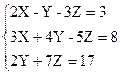
 , B =
, B = 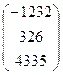
 , B =
, B = 
 , B =
, B = 
 , B =
, B = 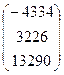
 , B =
, B = 
 , B =
, B = 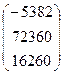
 , B =
, B = 
 , B =
, B = 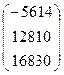
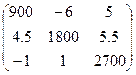 , B =
, B = 
 , B =
, B = 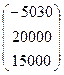
 , B =
, B = 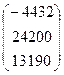
 , B =
, B =