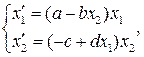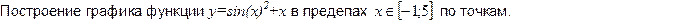Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное интегрирование. Численное решение обыкновенных дифференциальных уравненийСодержание книги
Поиск на нашем сайте
Численное интегрирование Если функция f(x) непрерывна на [ a,b ] и известна ее первообразная Ф(х), то определенный интеграл от этой функции вычисляется по формуле Ньютона-Лейбница:
Однако часто первообразная функция не может быть найдена с помощью элементарных средств или является слишком сложной, или подынтегральная функция задана таблично. В этих случаях применяются приближенные методы вычисления определенных интегралов. Обычный прием численного интегрирования состоит в том, что данную функцию f(x) на рассматриваемом промежутке заменяют интерполирующей функцией простого вида F(x), а затем приближенно полагают:
Метод прямоугольников Разобьем отрезок [ a,b ] на n равных промежутков точками x0, x1,…, xn. Величина h = (b-a)/n – длина каждого промежутка разбиения – называется шагом интегрирования. Заменим функцию f(x) на каждом промежутке постоянной функцией, принимающей значение, равное значению в левом (правом) конце промежутка. Получим при этом формулу левых (правых) прямоугольников (как площадь ступенчатой фигуры, образованной прямоугольниками). Формула левых прямоугольников:
Формула правых прямоугольников:
Справедлива следующая оценка погрешности формул прямоугольников:
Формула трапеции Величина интеграла может быть определена с большей точностью с тем же шагом интегрирования, если считать, что на каждом промежутке функция не постоянна, а изменяется линейно от значения в левом конце до значения в правом конце. Формула трапеции имеет вид:
Оценка точности формулы:
Формула Симпсона Формула Симпсона для многочленов 2 степени имеет вид:
Формула остаточного члена:
Задание 4.1. Вычислить значение определенного интеграла, заданного в таблице 2.
Таблица 2 – Задания для расчетов
Численное решение обыкновенных дифференциальных уравнений Дифференциальные уравнения и их системы можно решать численными методами (в частности, методом конечных разностей).
Решение заключается в нахождении ряда значений xi и y i искомой зависимости y(x) при i, изменяющемся от 0 до N при шаге изменения х, равном h. Будем рассматривать способы решения дифференциального уравнения, при которых h = const. Рассмотрим методы решения обыкновенных дифференциальных уравнений первого порядка вида Y' = f(X,Y). Mетод Эйлера Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений: xi+1=x1+h; yi+1=y1+h*f(x,y). (27) При этом для i = 0 значения x0 и y0 должны быть известны как начальные условия. Погрешность метода пропорциональна h2. Для уменьшения погрешности решения следует применять более точные методы. Например, метод Эйлера с пересчетом реализуется следующими итерационными выражениями на каждом шаге вычислений: xi+1=x1+h; yi+1=y1+h*(f(x1,y1)+f(x1+h,y1+h*f(x1,y1)))/2 (28) Погрешность метода пропорциональна h3. Метод Рунге-Кутта При высоких требованиях к точности решения можно воспользоваться методом Рунге-Кутта, реализующийся следующими формулами: k1 = h* f(xi,yi); k2 = h* f(xi+h/2,yi+k1/2); k3 = h* f(xi+h/2,yi+k2/2); (29) k4=h*f(xi+h,yi+k3); xi+1 = xi + h; yi+1 = yi + (k1+2*k2+2*k3+k4)/6. Погрешность метода пропорциональна h5. Для решения обыкновенных дифференциальных уравнений 2-го порядка Y''+p(x)Y'+g(x)Y=f(x) с граничными условиями: k11*Y(a)+k12*Y' (a)=A, k21*Y(b)+k22*Y´(b)=B также применяется метод конечных разностей, при этом производные, входящие в уравнение и дополнительные условия заменяются следующими конечно-разностными отношениями:
В результате получим систему алгебраических уравнений, решение которой даст таблицу приближенных значений искомой функции.
ПРИМЕР. Решить обыкновенное дифференциальное уравнение 2-го порядка: y''+xy'-0.5y/x=1
Решение: Разбив отрезок [2, 2.3] на части с шагом h = 0.1, получим четыре узловые точки с абсциссами x0 =2, x1 =2.1, x2 =2.2, x3 =2.3. Две точки x0 =2 и x3 =2.3 являются конечными, две другие – внутренними. Данное уравнение во внутренних точках заменим конечно-разностным:
Из краевых условий составим конечно-разностные уравнения в конечных точках:
Задача сводится к решению системы уравнений:
Примеры решения дифференциальных уравнений с помощью встроенных функций системы MathСad приведены в приложениях Д, Е. Задание 4.2. Решите на отрезке [ x0,xend ] задачу Коши
Таблица 3 – Данные для расчета
Порядок выполнения задания: 1. Присвойте начальное значение решения переменной у0. 2. Определите правую часть уравнения f(x,y). 3. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 4. Сохраните решение в матрице У1. 5. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 2 6. Сохраните решение в матрице У2. 7. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 8. Сохраните решение в матрице У3. 9. Постройте на одном графике все три найденных решения. 10. Оцените погрешности найденных решений по формуле Рунге.
Задание 4.3. Решите задачу Коши
Таблица 4 – Данные для расчета
Продолжение таблицы 4
Порядок выполнения задания: 1. Присвойте переменной ORIGIN значение, равное единице. 2. Присвойте начальное значение решения переменной у0. 3. Определите правую часть уравнения f(x,y). 4. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 5. Сохраните решение в матрице У1. 6. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 2 7. Сохраните решение в матрице У2. 8. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 9. Сохраните решение в матрице У3. 10. Постройте на одном графике все три найденные решения. 11. Оцените погрешности найденных решений по формуле Рунге. Задание 4.4. Найдите общее решение линейного однородного уравнения второго порядка Таблица 5 – Данные для расчета
Порядок выполнения задания: 1. Присвойте переменной ORIGIN значение, равное единице. 2. Присвойте начальное значение решения переменной у0. 3. Определите правую часть уравнения f(x,y). 4. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 5. Сохраните решение в матрице У1.
Задание 4.5. Постройте графики решения и фазовые портреты динамической системы
моделирующей взаимодействие популяций при заданных значениях параметров a,b,c,d. Значения параметров заданы в таблице 6. Исследуйте поведение решения, изменяя параметры. Таблица 6 – Данные для расчета
Порядок выполнения задания: 1. Присвойте переменной ORIGIN значение, равное единице. 2. Определите вектор-столбец начальных условий для первой задачи Коши. 3. Определите вектор-столбец правых частей системы. 4. Выберите значение шага интегрирования h и вычислите количество шагов N интегрирования системы на отрезке [ x0,xend ] по формуле N= 5. Решите задачу Коши для первого начального условия. 6. Изобразите соответствующую фазовую кривую и график решения. 7. Определите векторы-столбцы начальных условий для каждого начального условия. 8. Решите соответствующие задачи, сохранив каждое решение в отдельной матрице. 9. Изобразите соответствующие фазовые кривые и графики решений.
Задание 5.5. Исследуйте поведение системы
моделирующей взаимодействие популяций. Выполните вычисления для значений a,b,c,d из задания 7.4 для приведённых ниже значений a (таблица 7). Таблица 7 – Данные для расчета
Список Литературы
1. Кудрявцев, Е.М. MathCad 8 / Е.М. Кудрявцев - М: ДМК, 2000. - 320с. 2. Плис, А.И. MathCad 2000: математический практикум для экономистов и инженеров: Учебное пособие / А.И. Плис, Н.А. Сли-вина - М.: Финансы и статистика, 2000. - 656с. 3. Турчак, Л.И. Основы численных методов: Учеб. пособие / Л.И. Тучак - М.: Физматлит., 2003. -304с. 4. Информатика: Учеб. пособие / А.В. Могилев, Н.И. Пак, Е.К. Хеннер; Под ред. Е.К. Хеннера. - М.: Издат. центр «Академия», 2004. - 848с. 5. Шуп, Т. Решение инженерных задач на ЭВМ / Т. Шуп - М.: Мир, 1982. -240с.
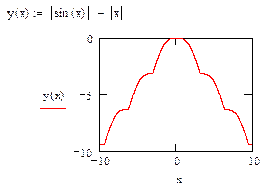
Приложение А Построение графиков
Приложение Б
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.92.87 (0.012 с.) |

 . (10)
. (10)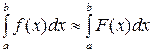 . (11)
. (11) . (12)
. (12)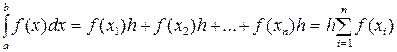 . (13)
. (13) ;
; (14)
(14) . (15)
. (15)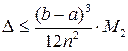 ;
;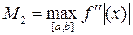 . (16)
. (16) (17)
(17)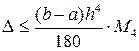 ;
;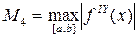 (18)
(18)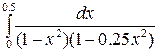

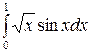

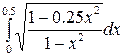
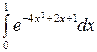
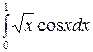
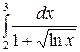
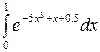
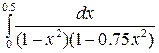
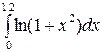
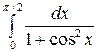
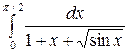
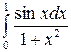
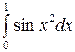

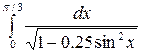
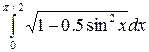
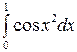




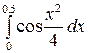
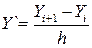 ;
; 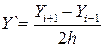 ;
; 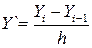 ; (30)
; (30) . (31)
. (31)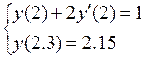
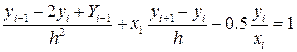 (i= 1, 2).
(i= 1, 2). , y3=2.15.
, y3=2.15.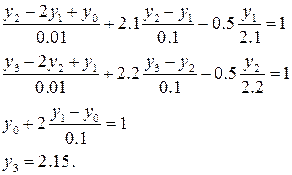
 методом Рунге-Кутта с постоянным шагом. Вид уравнения и начальные значения заданы в таблице 3. Изобразите графики решений, вычисленных с шагами h, 2 h и h /2.
методом Рунге-Кутта с постоянным шагом. Вид уравнения и начальные значения заданы в таблице 3. Изобразите графики решений, вычисленных с шагами h, 2 h и h /2.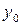
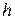
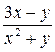



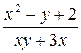
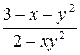
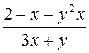
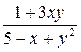

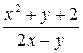

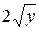
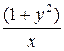
 .
.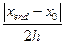 .
.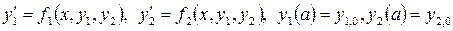 на отрезке [ a,b ] методом Рунге-Кутты с постоянным шагом h =0.1. Изобразите графики решений, вычисленных с шагом h, 2 h и h /2. Вид уравнений и начальные значения заданы в таблице 4.
на отрезке [ a,b ] методом Рунге-Кутты с постоянным шагом h =0.1. Изобразите графики решений, вычисленных с шагом h, 2 h и h /2. Вид уравнений и начальные значения заданы в таблице 4.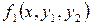
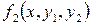
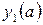
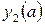

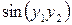

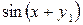

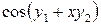
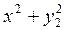




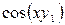
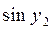
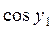
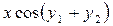
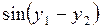
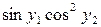
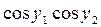
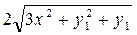

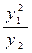

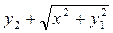

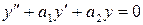 . Решите задачу Коши
. Решите задачу Коши 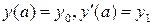 . Изобразите его график. Значения параметров а1, а2 и а заданы в таблице 5.
. Изобразите его график. Значения параметров а1, а2 и а заданы в таблице 5.