
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы обработки экспериментальных данных
Предположим, что в результате измерений в процессе экспериментов были получены n пар значений: (x1, y1), (x2, y2), …, (xn, yn). Задача состоит в том, чтобы найти приближенную зависимость y = f(x), значения которой при x = xi(i=1,…,n) мало отличаются от опытных данных yi. Определение 1. Приближенная функциональная зависимость, полученная на основании экспериментальных данных, называется ЭМПИРИЧЕСКОЙ ФОРМУЛОЙ. Построение эмпирической формулы состоит из двух этапов: подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров. Общий вид формулы обычно выбирается из геометрических соображений: экспериментальные точки наносятся на график, и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, показательной или логарифмической функции и т.п.). Когда тип эмпирической формулы выбран, ее можно представить в виде: y=f(x,a1,a2,…,am). (20)
где f – известная функция, a1,a2,…,am – неизвестные постоянные параметры, необходимо определить такие значения этих параметров, которые дают наилучшее приближение. Определение 2. ОТКЛОНЕНИЕМ ei называется разность между значениями эмпирической функции (20) в точках x1 (i =1,…,n) и опытными данными yi: ei=f(xi,a1,a2,…,am)-yi . (21)
Задача нахождения наилучших значений параметров сводится к некоторой минимизации отклонений ei. Существует несколько методов решения этой задачи. Метод выбранных точек Он состоит в следующем: на примерном графике эмпирической функции выбираются точки, число которых равно количеству искомых параметров. Координаты этих точек тщательно измеряются для записи условия прохождения графика через выбранные точки. Из полученной таким образом системы уравнений находят значения параметров a1, a2,…, am Метод средних Рассмотрим еще один способ определения параметров эмпирической формулы – метод средних. Он состоит в том, что параметры a1, a2,…, am зависимости (20) определяются с использованием условия равенства нулю суммы отклонений (21) во всех точках xi:
Полученное уравнение служит для определения параметров a1, a2,…, am. Метод наименьших квадратов Запишем сумму квадратов отклонений для всех точек x1, x2,…, xn:
Параметры a1, a2,…, am эмпирической формулы (20) будем находить из условия минимума функции S. В этом состоит метод наименьших квадратов. Минимум функции находим из условия равенства нулю частных производных по всем параметрам:
Полученные соотношения - система линейных уравнений для опреде-ления неизвестных параметров. Например, для линейной функции y = ax + b эта система имеет вид:
В системе MathCad существуют встроенные функции для вычисления коэффициентов а и b линейной зависимости y=ax+b: - slope(x,y) - возвращает значение коэффициента а; - intercept(x,y) - возвращает значение коэффициента b. Формулы для вычисления коэффициентов а и b линейной зависимости можно применять для нахождения параметров эмпирических функций, график которых не является прямой линией. Так, если эмпирическая формула имеет вид степенной функции y=kxm, то, введя обозначения У=lny и X=lnx можно воспользоваться формулами для вычисления коэффициентов а и b линейной зависимости и выразить через них значения коэффициентов k и m: k=eb и m=a . Если эмпирическая формула имеет вид показательной функции y=peqx, то, введя обозначения У=lny и X=x и вычислив коэффициенты а и b линейной зависимости, можно выразить через них значения коэффициентов p и q: p=eb и q=a . Примеры построения эмпирических формул даны в приложении Г.
Задание 3.4. По заданным экспериментальным данным найти параметры эмпирических формул (y=ax+b, y=kxm, y=peqx, y=alnx+b)методомнаименьших квадратовс помощью встроенных функций MathCad. Построить графики полученных функций. Выбрать наилучшее приближение и найти значение у в точке х=n +0.55, где n - номер варианта.
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
Порядок выполнения задания: 1. Ввести значения векторов х и y. 2. Вычислить коэффициенты a1 и b1 аппроксимирующей прямой у1(х), используя формулы slope(x,y) и intercept(x,y). 3. Вычислить коэффициенты k и m степенной функции y2(х)=kxm, предварительно введя новые переменные У и X и вычислив коэффициенты а2 и b2 линейной зависимости, используя формулы slope(Х,У) и intercept(Х,У). 4. Вычислить коэффициенты p и q показательной функции у3(х)= peqx, предварительно введя новые переменные У и X и вычислив коэффициенты а3 и b3 линейной зависимости. 5. Вычислить коэффициенты a4 и b4 показательной функции у4(х)=a4lnx+b4, предварительно введя новые переменные У и X. 6. Изобразите на графике заданные экспериментальные точки Уi и функции у1(хi), у2(хi), у3(хi), у4(хi) и выберите наилучшее приближение. 7. Найдите значение функции в указанной точке.
Лабораторная работа №4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.67.225 (0.01 с.) |
 (22)
(22)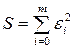 (23)
(23)
 …
… 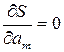 (24)
(24) (25)
(25)


