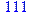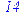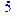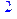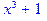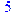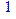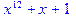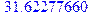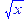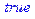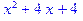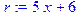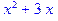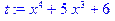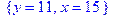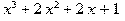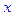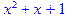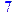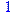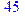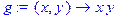Численное решение системы уравнений

Результатом решения системы будет численное значение искомого корня. Для численного решения системы уравнений выполните следующее:

1). Задайте начальные приближения для всех неизвестных, входящих в систему уравне­ний. Mathcad решает уравнения при помощи итерационных методов, в которых начальное приближение определяет корень, который найдёт Mathcad.

2). Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений..

3). Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Для ввода знака булева равенства "=" в уравнения используйте панель инструментов Boolean или сочетание клавиш <Ctrl+=>.

4). Введите выражение, которое включает функцию Find.

Find (x, y...) - возвращает численные значения x, y..., которые удовлетворяют уравнениям и неравенствам, находящимся в блоке решений. Если вы решаете систему N переменных, то блок решений должен содержать N уравнений.

x,y... - скалярные переменные, находящиеся в системе уравнений.

Функция Find возвращает скаляр, если блок решения содержит одну неизвестную. В про­тивном случае функция возвращает вектор, первый элемент которого x, второй элемент - y, и так далее

В блоке решения недопустимы следующие выражения:

1). Выражения со знаком ≠.

2). Выражения, содержащие оператор присваивания (":=").

3). Неравенства вида a<b<c.

Если в процессе решения уравнений на каком-либо шаге итераций не может быть найдено более приемлемое приближение к искомому решению по сравнению с предыдущим шагом, то поиск решения прекращается, а функция Find помечается со­общением об ошибке 'did not find solution ' ('решение не найдено').

Причиной появления этого сообщения об ошибке может быть следующее:

1). Поставленная задача может не иметь решения.

2). Для уравнения, которое не имеет вещественных корней, в качестве начального при­ближения взято вещественное число. Если решение задачи комплексное, то оно будет найдено, только если в качестве начального приближения взято комплексное число.

3). В процессе поиска решения достигнута точка из которой невозможно выбрать подхо­дящее направление спуска - направление вдоль которого ищется следующее приближение. Для поиска искомого решения пробуйте использовать различные начальные приближения или до­бавьте ограничения на переменные в виде неравенств, чтобы миновать нежелательную точку остановки.

4). Возможно, поставленная задача не может быть решена с заданной точностью. Попро­буйте уменьшить значение встроенной переменной TOL в меню Math\Options\Built-in Variables.

Символьное решение систем уравнений

Для символьного решения уравнения необходимо использовать блоки символьного реше­ния (Уравнения и неравенства, находящиеся между Given и Find, называют блоком решения).

При символьном решении системы уравнений искомый корень выражается через другие переменные и константы.

Чтобы решить систему уравнений символьно, необходимо выполнить следующее:

1). Введите ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.

2). Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Для ввода знака булева равенства "=" в уравнения используйте панель инструментов Boolean или сочетание клавиш <Ctrl+=>.

3).Введите функцию Find, в скобках укажите все искомые аргументы.

4). Нажмите <Ctrl+.> (клавиша Ctrl, сопровождаемая точкой). Mathcad отображает символьный знак равенства.

Щёлкните мышью вне выражения. Mathcad вернёт ответ в виде вектора решений

 

Завдання на лабораторну роботу

1. Вирішити систему лінійних рівнянь чисельно та символьно (табл. 1).

2. Знайти екстремальні значення функції на відрізку (табл. 2).

3. Вирішити систему нелінійних рівнянь чисельно та символьно (табл. 3).

4. Виконати завдання N та (35-N) (Додаток).

При виконанні завдання номер варіанту N обирається згідно з номером комп’ютера

ЛАБОРАТОРНА РОБОТА № 7

Математичний пакет Maple.

Мета роботи: ознайомитися з пакетом математичних обчислень Maple.

Використовуване програмне забезпечення: пакет математичних обчислень Maple.

2.1 Теоретичні відомості

Робота c Help

Для того щоб одержати інформацію про використання деякої функції, необхідно набрати ім'я функції в командному рядку Maple і натиснути <Ctrl+F1>.

Для отримання довідки по підрозділу необхідно вибрати пункти меню

Help=> Introduction

і вибрати розділ, мандруючи по деревоподібній структурі меню.

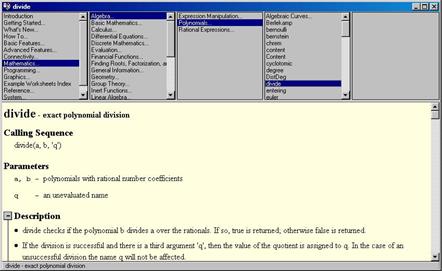
Рисунок 2.1 – Основне вікно довідки в Maple

Елементи синтаксису мови:

1.2.6.1 %	1.2.6.2 –	1.2.6.3 системна змінна, що зберігає результат попередньої операції;
1.2.6.4:	1.2.6.5 –	1.2.6.6 фіксатор виразу, що запобігає виводу результатів обчислення поточного виразу на екран;
1.2.6.7;	1.2.6.8 –	1.2.6.9 фіксатор виразу, що дозволяе відображення результатів обчислення поточного виразу на екран;
1.2.6.10 #	1.2.6.11 –	1.2.6.12 покажчик програмного коментарю;
1.2.6.13 "	1.2.6.14 –	1.2.6.15 обмежувач рядка (наприклад, 'string');
1.2.6.16:=	1.2.6.17 –	1.2.6.18 оператор присвоювання (наприклад, х:=5);
1.2.6.19:;	1.2.6.20 –	1.2.6.21 порожній оператор;
1.2.6.22::	1.2.6.23 –	1.2.6.24 покажчик типу змінної (наприклад, n::integer або z::complex);
1.2.6.25 \	1.2.6.26 –	1.2.6.27 знак оберненого ділення, що приймає значення в залежності від контексту (див. довідку по цьому знаку backslash).

Масиви, вектори і матриці

Одним із типів даних є списки (lists). Вони створюються за допомогою квадратних скобок, наприклад:

· [1,2,3,4] - список із чотирьох цілих чисел;

· [1.,2.34,5] - список із двох дійсних і одного цілого числа;

· [а,b,'Привіт'] - список із двох символів (змінних) і строкової константи;

· [sin(x), 2*cos(x), a^{^}2–b] — список із трьох математичних виразів.

Вектори і матриці є окремим типом даних. Для створення векторів (одномірних масивів) і матриць (двумірних масивів) служить функція array. Звичайно вона використовується в таких формах:

· аrrау[а..b,s1] — повертає вектор з індексами від а до b і значеннями в одномірному списку s1;

· аrrау[а..b,c..d,s2] — повертає матрицю з номерами рядків від а до b, номерами стовпчиків від c до d і значеннями в двумірному списку s2.

Елементами векторів і масивів можуть бути константа, змінні, вирази, списки й інші об'єкти. Ці елементи є індексованими змінними, і їх положення вказується індексами.

Деякі функції Maple

Функція сonvert - перетворення уявлення числа.

За допомогою функції convert Maple може перетворювати числа в уявлення з різноманітною основою (від 2 до 36, у тому числі бінарною і шістнадцятирічною), наприклад:

 

> convert(7,binary);

> convert(20,hex);

> convert(101, decimal, binary);

При символьних обчисленнях Maple реалізує точну арифметику. Це значить, що результат може бути отриманий із будь-яким числом цифр. Проте треба пам'ятати, що ідеально точні чисельні обчислення виконуються тільки у випадку цілочисельних операцій.

 

Оператор mod - обчислення в кільці цілих чисел за модулем m.

 

E mod m

Modp(e, m)

Параметри:

e – алгебраїчний вираз

m – невід’ємне число, модуль перетворень

 

Оператор mod обчислює вираз e над кільцем цілих чисел за модулем m.

Оператор mod можуть використовувати наступні функції для поліноміальної і матричної арифметики над скінченними кільцями і полями

Content, Det, DistDeg, Divide, Eval, Expand, Factor, Factors, Frobenius, Gausselim, Gaussjord, Gcd, Gcdex, Hermite, Interp, Inverse, Issimilar, Lcm, Normal, Nullspace, Power, Powmod, Prem, Primfield, Primitive, Primpart, Quo, Randpoly, Randprime, Rem, Resultant, Roots, Smith, Sprem, Sqrfree, taylor.

Приклади:

> 17 mod 5;

> x^3+10*x+1 mod 5;

> 1/3 mod 7;

> 5*3 mod 7;

> modp(55,7);

> modp(x^12+x+19,3);

> g:= Gcd(a,b) mod 11;

> Divide(a,g,'q') mod 11;

Функція sqrt - обчислення квадратного кореня.

Sqrt(x)

Параметри:

x - алгебраїчний вираз

Приклади:

> sqrt(1000);

> sqrt(1000.0);

> sqrt(x);

> sqrt(-9*x^2*y);

Функція Divide - перевірка подільності многочленів

 

Divide(a, b, 'q')

Параметри:

a, b - поліном;

q - (необов'язковий параметр) ім'я змінної

Функція Divide перевіряє, чи ділиться a на b без залишку. В змінну q поміщається результат ділення у випадку успіху.

Приклади:

> Divide(x^3+x^2+2*x+3, x+2, 'q') mod 5;

> q;

Функція Rem - виділення залишку від ділення многочленів.

Функція Quo - виділення неповної частки від ділення многочленів.

Rem(a,b,x)

Rem(a,b,x,'q')

Quo(a,b,x)

Quo(a,b,x,'r')

Параметри:

x - ім'я змінної в многочленах

a, b - многочлени від змінної x

q, r - імена змінних

Два поліноми a і b (степінь a > степеня b) пов'язані таким співвідношенням.

a = b*q + r.

Тут r - залишок, а q - неповна частка від ділення a на b.

Якщо використовувати дані функції разом з оператором mod p, ділення буде виконуватися над кільцем цілих чисел за модулем p.

Приклади:

> a:= x^4+5*x^3+6:

> b:= x^2+2*x+7:

> r:= Rem(a,b,x,'q') mod 13;

> q;

> s:= Quo(a,b,x,'p') mod 13;

> p;

> t:=Expand((x^2+2*x+7)*(x^2+3*x)+(5*x+6)) mod 13;

Процедура msolve – розв’язання рівнянь у Z_m.

Msolve(eqns,vars,m)

Msolve(eqns,m)

Параметри:

eqns – одне або система рівнянь;

vars - (необов'язковий параметр) одне або набір імен;

m - ціле число, модуль перетворень.

Процедура msolve розв’язує рівняння в eqns у цілих числах за mod m. Повертається NULL якщо не існує розв’язків у цілих числах за mod m.

Приклади:

> msolve({3*x-4*y=1,7*x+y=2},19);

> msolve(x^2=3,5); # Немає рішень

 

Функція Expand - розкриває скобки і подає добуток у вигляді суми.

Expand(a)

Параметри:

а - будь-який алгебраїчний вираз.

 

Приклади:

> Expand((x+2)^2*(x-2)) mod 3;

 

 

Функція Powmod - зведення многочлена в степінь за модулем іншого многочлена.

Powmod(a, n, b, x)

Powmod(a, n, b)

 

Параметри:

a - многочлен від x

n - ціле число

b - многочлен від x

x - ім'я змінної

Функція Powmod обчисляєa^n mod b, де a і b - многочлени від x, n-ціле (показник степені, можливо від’ємне).

Приклади:

> Powmod(x,16,x^4+x+1,x) mod 2;

> Powmod(x,-5,x^4+x+1,x) mod 2;

Програмування в Maple

Умовні вирази if.

Для підготування програм, що розгалужуються, у Maple-мову програмування включений оператор if, що дозволяє створювати таку конструкцію:

 

if <Умова порівняння> then <Елементи>

|elif < Умова порівняння> then <Елементи>|

|e1se <Елементи>|

fi:

 

У вертикальних рисках | | зазначені необов'язкові елементи даної конструкції.

 

> a:= 7; b:= 3;

> if (a > b) then a else b end if;

Цикли for і while.

Найчастіше необхідно циклічне повторення виконання виразу задане число раз або доти, поки виконується визначена умова. Maple має узагальнену конструкцію циклу, що задається в такий спосіб:

 

 

| for <name>| |from <exprl>| |to <expr2>| |by <expr3>|

| while <expr4>|

do <statement sequence> od;

 

Тут name - ім'я керуючої змінної циклу, exprl, ехрr2 і ехрr3 - вирази, що задають початкове значення, кінцеве значення і крок змінної name, ехрr4 - вираз, що задає умову, доки цикл (набір об'єктів між словами do і od) буде виконуватися.

У ході виконання циклу керуюча змінна змінюється від значення exprl до значення ехрr2 із кроком, заданим ехрr3. Якщо блок by <ехрr3> відсутній, то керуюча змінна буде змінюватися з кроком +1. Наприклад:

> for i from 1 to 3 do print(i): od;

Прості процедури.

 

Процедурою називають модуль програми, що має самостійне значення і виконує одну або декілька операцій, звичайно достатньо складних і відмінних від операцій, виконуваних вбудованими операторами і функціями.

Процедури визиваються так само, як вбудовані функції, - по імені зі списком фактичних параметрів. При цьому процедури звичайно не повертають ніяких значень після свого виконання, хоча можуть привласнювати значення вхідним змінним.

Найпростіша форма завдання процедури така:

name:=рrос(Параметры)

Тіло процедури

end;

При виклику процедури вираженням виду:

name(Фактичні_параметри)

фактичні параметри підставляються на місце формальних. Невідповідність фактичних параметрів типу заданих змінних веде до повідомлення про помилку і до відмови від виконання процедури.

Приклад процедури:

> Fun:=proc(x,y)

x*y;

end:

> Fun(5,9);

Процедури-функції у відповідь на виклик до них повертають деяке значення. Вони як би є новими функціями, що задаються користувачем. Процедуру-функцію можна задати за допомогою функціонального оператора ”->”.

Наприклад:

> g:= (x,y) -> x*y;

> g(1,2);