
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоматизація математичних розрахунків засобами пакету mathcadСодержание книги
Поиск на нашем сайте
О.М.Дудка
АВТОМАТИЗАЦІЯ МАТЕМАТИЧНИХ РОЗРАХУНКІВ ЗАСОБАМИ ПАКЕТУ MathCAD Навчальний посібник Є доп. видання
Івано-Франківськ -2004- ВСТУП Широке впровадження електронно-обчислювальної техніки в найрізноманітніших галузях людської діяльності поставило на порядок денний вимогу, щоб фахівець будь-якої професії вмів використовувати нові інформаційні технології в своїй практичній діяльності. Впровадження в навчальний процес сучасних засобів збирання, зберігання, опрацювання, подання, передавання інформації відкриває широкі перспективи щодо гуманітаризації освіти і гуманізації навчального процесу, поглиблення та розширення теоретичної бази знань і надання результатам навчання практичного значення, активізації пізнавальної діяльності, створення умов для повного розкриття творчого потенціалу людини з урахуванням її вікових особливостей і життєвого досвіду, індивідуальних нахилів, запитів і здібностей. На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв'язувати за допомогою комп'ютера досить широке коло математичних задач різних рівнів складності. Причому одні з цих програм розраховані на фахівців досить високої кваліфікації в галузі математики, інші - на учнів середніх навчальних закладів чи студентів вузів, які лише почали вивчати шкільний курс математики чи основи вищої математики. Серед цих програм такі як DERIVE, EUREKA, GRAN1, Maple, Mathematika, MathLab, Maxima, Numeri, Reduce, Statgraph, MathCA. Використання програм дає можливість розв'язувати окремі задачі, не знаючи відповідного аналітичного апарату, методів і формул, правил перетворення виразів тощо. Використання подібних програм дає можливість у багатьох випадках зробити розв'язування задач настільки ж доступними, як і просте розглядання малюнків чи графічних зображень. Відповідні програми перетворюють окремі розділи і методи математики в «математику для всіх», що робить їх доступними, зрозумілими, легкими і зручними для використання, а той, хто розв'язує задачу, стає користувачем математичних методів, можливо не володіючи їхньою будовою і обгрунтуванням, аналогічно до того, як він використовує інші комп'ютерні програми (текстові, графічні, музичні редактори, електронні таблиці, бази даних, операційні оболонки, експертні системи), не знаючи, як і за якими принципами вони побудовані, якими мовами програмування описані, які теоретичні положення покладено в їхню основу.
З іншого боку, такий підхід до вивчення математики дає наочні уявлення про поняття, що вивчаються, розвиває образне мислення, просторову уяву, дозволяє досить глибоко проникнути в сутність досліджуваного явища, неформально розв'язувати задачу. При цьому на передній план виступає з'ясування проблеми, постановка задачі, розробка відповідної математичної моделі, матеріальна інтерпретація отриманих за допомогою комп'ютера результатів. Усі технічні операції щодо опрацювання побудованої математичної моделі, реалізації методу відшукання розв'язку, оформлення та подання результатів опрацювання вхідної інформації покладаються на комп'ютер. Важко переоцінити ефективність використання програм зазначеного типу і в разі поглибленого вивчення математики. Можливість провести необхідний чисельний експеримент, швидко виконати потрібні обчислення чи графічні побудови, перевірити ту чи іншу гіпотезу, випробувати той чи інший метод розв'язування задачі, вміти проаналізувати та пояснити результати, отримані за допомогою комп'ютера, з'ясувати межі можливостей застосування комп'ютера чи обраного методу розв'язування задачі має надзвичайне значення у вивченні математики. Розглянемо зокрема пакет MathCAD for Windows(Mathematical Computer Aided Design – математичне автоматизоване проектування) фірми Mathsoft Inc. Пакет MathCAD є унікальною системою для роботиз числами, формулами, текстами і графіками. Пакет є гнучкий та надійний, цікавий для вивчення та достатньо простий у користуванні. Він надає користувачу одночасно можливості електронної таблиці і текстового процесора. Як у електронних таблицях будь-яка зміна вмісту робочого документу MathCAD for Windows викликає поновлення, перерахунок всіх залежних результатів, в тому числі і перерисовку графіків. Дозволяє читати дані із файлів і виконувати над ними довільні математичні перетворення. Подібно до текстового процесора MathCAD for Windows має інтерфейс wysiwyg (What You See Is What You Get – що ви бачите, те і одержите), множину різних шрифтів і можливість друкувати те, що зображено на екрані дисплея, на будь-якому принтері, робота якого підтримується системою Windows.
MathCAD – не тільки засіб для вирішення різного роду математичних задач. Це, по суті, потужна математична САПР (система автоматизованого проектування), яка дозволяє готувати на найвищому поліграфічному рівні любі матеріали, які відносяться до науки і техніки: документацію, наукові звіти, книги і статті, дисертації, дипломні і курсові проекти. При цьому в них одночасно можуть бути складні тексти, різні математичні формули, складні обчислення, графіки функцій і ілюстративні матеріали. Пакет дозволяє готувати високоякісні електронні книги з гіпертекстовими посиланнями. Даний навчальний посібник побудовано як конспект лекцій з лабораторними роботами для методичного забезпечення курсу “Автоматизація математичних розрахунків”, який би сприяв закріпленню теоретичного матеріалу і розвитку практичних навиків при розв’язанні різноманітних математичних задач не тільки шкільного курсу, а й при розв’язуванні задач, які вимагають досить високої кваліфікації в галузі математики, зокрема таких як “Математичний аналіз” – знаходження інтегралів і диференціалів, обчислення сум рядів, “Алгебра” – перетворення, транспонування, обчислення визначників і матриць, “Елементарна математика” – розклад виразів на множники і зведення до найпростішого виду, розв’язування рівнянь і нерівностей, побудова графіків та ін. Даний матеріал може бути використаний викладачами і студентами технічних, математичних, економічних, фізичних спеціальностей інститутів та університетів. Розділ 1. Пакет MathCAD як засіб автоматизації математичних розрахунків Робота з текстом Текстові коментарі в системі MathCAD мають важливе значення, оскільки розв’язуючи ту чи іншу задачу без жодних коментаріїв, через деякий час важко згадати, що саме ми робили в документі. Для введення тексту використовується символ ” (одні подвійні лапки) або команда Текстова область пункту Вставка головного меню. Після цього з’явиться прямокутник (текстова область), де вводиться текст. Текст редагується загальноприйнятими засобами, аналогічно до всіх сучасних текстових редакторів. Для завершення вводу тексту достатньо вийти за межі текстової області або клацнути мишкою за її межами. Нерідко користувач починає набір тексту, забувши встановити признак текстової області (одні подвійні лапки). MathCAD 2001 сприймає такий набір як введення математичного виразу. Однак, натиснувши клавішу Пропуск, набраний фрагмент перетворюється в текстовий. Текстова область в процесі набору тексту розширюється. Область має маркери зміни розміру у вигляді маленьких чорних прямокутників, за допомогою яких можна змінити розміри текстової область. Кодування представлення <x> {:} <1>,<3>;<100> x:= 1,3.. 100 Пакет володіє багатьма стандартними функціями. Для того щоб задати функцію, необхідно в пункті меню Вставка вибрати підпункт Функція і, вибравши потрібну функцію, натиснути “OK”, або натиснути піктограму f(x) на панелі інструментів Стандартна і, вибравши потрібну функцію, натиснути “OK”, або кодувати вручну, через клавіатуру. В пакеті MathCAD аргумент тригонометричних функцій береться в радіанах. Для того, щоб MathCAD аргумент тригонометричних функцій брав в градусах, треба обчислювати тригонометричні функції від (аргумент*deg). Також MathCAD підтримує функції матричного та векторного аргументу. Для введення і визначення вектора чи матриці використовується команда Матриця пункту меню Вставка, чи кнопка Матриці з панелі інструментів Математика. В результаті з’явиться вікно з двома полями, в яких треба вказати кількість рядків і стовпців. Після цього з’являється макет матриці з покажчиками, куди треба записати елементи матриці. Звернення до елементів масиву (матриці) здійснюється заданням імені масиву і індексу елемента, який вводиться через кому. Індекс вводиться клавішою “[”, або кнопкою Індекс з панелі інструментів Математика. Перший рядок і стовпчик матриці позначаються по замовчуванню як нульові.
Також MathCAD підтримує можливість створення функції користувача. Функція користувача – це функція якій ми присвоюємо якийсь вираз. Дальше, при роботі з цим виразом ми вже не записуємо його, а тільки ім’я функції, яку ми задали і список аргументів. Функція користувача дійсна тільки в межах поточного документа. Перед використанням вона повинна бути оголошена (визначена). Формат оголошення функції користувача: <Ім’я функції>(список аргументів):= <вираз> Приклад: Нехай, в документі кілька разів потрібно обчислити значення виразу а потім, вже не записуючи цілий вираз, а тільки ім’я даної функції і список змінних від яких вона залежить, в даному випадку В пакеті прийнято звичайний порядок обчислень зліва направо і зверху вниз. Тому операція присвоєння (:=) носить лише локальний характер. Її дія розповсюджується лише на конструкції, що розташовані правіше і нижче. Побудова двомірних графіків Для створення області графіка потрібно курсор встановити у вільну частину документа і натиснути клавішу “@”, або вибрати в панелі інструментів Математика кнопку Графіки та кнопку Двомірний графік. Після цього у вказаному місці з’являється порожня графічна область з 6 покажчиками (Рис.1). Курсор встановлюється в покажчик 2 осі ОХ. В цій позиції, як правило, задається ім’я ранжованої змінної, а в позиціях 1 і 3 відповідно початок і кінець діапазону зміни її значень. В позиції 5 задається ім’я ранжованого виразу, якщо він був означений раніше, або просто права частина даного виразу, а в позиціях 4 і 6 відповідно початок і кінець діапазону зміни його значень.
6■ 5■ 4■ ■ 1 ■ 2 ■ 3 Рис. 1
Покажчики 1, 3, 4, 6 можна не заповнювати. Тоді пакет сам вибирає оптимальні значення початку і кінця діапазону. Після виводу курсору з графічної області або натиснення клавіші “ Enter ” пакет виводить графік на екран. Для побудови декількох графіків на одному рисунку достатньо через кому ввести імена ранжованих виразів, чи самі вирази. Побудова графіків поверхонь Для побудови графіка поверхні потрібно: а) задати функцію від двох змінних; в) встановити курсор в те місце документа, де будемо будувати графік і натиснути [Ctrl]+[2], або вибрати в панелі інструментів Математика кнопку Графіки та кнопку Графік поверхні. Після цього з’являється порожня графічна область з одним покажчиком (■); г) ввести ім’я функції в покажчик (■) графічної області без списку змінних; д) після виводу курсора з графічної області або натиснення клавіші “ Enter ” пакет виводить графік на екран. Символьна математика Іноді, розв’язуючи задачі, нам потрібно не просто чисельно обчислити ту чи іншу функцію при якихось конкретних значеннях змінних, а проводити з ними символьні обчислення. Символьними називаються такі обчислення, результати яких представляються в аналітичному вигляді, тобто у вигляді формул. Системи, які проводять символьні обчислення, володіють так званим символьним процесором. Його основою є ядро, яке містить сукупність формул і формульних перетворень, з допомогою яких і проводяться аналітичні (символьні) обчислення. Команди, що відносяться до роботи символьного процесора, знаходяться в пункті Символи головного меню. Щоб виконати символьну операцію, процесору потрібно вказати, над яким виразом вона повинна проводитись, тобто треба виділити вираз. Для ряду операцій треба не тільки вказати вираз до якого відноситься операція, але й вказати змінну, відносно якої виконується символьна операція. Сам вираз в такому випадку не виділяється. Символьні обчислення мають два важливі аспекти: Вони виконуються тільки над явними виразами, тому присутність в виразах функцій користувача не можлива; Результат може виводитись нижче початкового виразу, справа від нього чи замість нього (спосіб виводу задається командою Стиль обчислень, меню Символи). Аналогічно знаку “=” при чисельному обчисленні, при символьному обчисленні виразу використовується знак “→”. Його можна ввести, вибравши в панелі інструментів Математика, кнопку Символьні оператори та кнопку Символьне обчислення. Різні символьні операції можна проводити з цілими виразами, чи з окремими змінними.
Обчислення похідних В середовищі пакету відбувається як символьне так і чисельне обчислення значень m-кратних похідних (m>1) і частинних похідних функцій у заданих точках. Для здійснення операції диференціювання потрібно натиснути клавішу знака запитання “?”, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку похідної. В результаті на екрані генерується знак операції з двома покажчиками:
Покажчик, що стоїть в знаменнику, вимагає означення змінної диференціювання, тоді як активний покажчик – функцію (її вираз чи ім’я), що диференціюється. Змінна диференціювання і всі константи та змінні, що входять у функцію повинні бути попередньо означені. Знак операції похідної вищого порядку може бути генерований кількаразовим натиском клавіші “?” по необхідності, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку Похідна N-го порядку. В результаті на екрані генерується знак операції з чотирма покажчиками:
В якості змінних диференціювання, констант і змінних диференційованої функції можуть виступати і ранжовані змінні. Дана можливість пакету дозволяє, наприклад, виводити графік похідної будь-якої плоскої функції або частинної похідної в заданій січній площині.
Обчислення інтегралів Пакет дозволяє символьно та чисельно обчислювати як звичайні, так і криволінійні інтеграли, крім того, серед них – багато інтегралів, підінтегральні функції яких мають особливості на кінцях відрізка інтегрування. Для вводу знаку операції інтегрування потрібно натиснути клавішу “&”, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку Визначений інтеграл. В результаті на екрані з’явиться знак операції з чотирма покажчиками:
Для означення і обчислення інтеграла необхідно замість активного покажчика задати підінтегральну функцію, після знака диференціала (d) потрібно означити змінну інтегрування, а замість покажчиків, що є знизу і зверху знаку інтеграла, вказати дійсні вирази, які визначають відповідно значення нижньої і верхньої меж інтегрування. В якості меж інтегрування повинні бути тільки дійсні вирази, тоді як підінтегральна функція може бути як дійсною, так і комплексною. Крім змінної інтегрування (ім’я якої повинне задовольняти умови пакету), інші змінні і константи, які використовуються в конструкції, повинні бути попередньо означені. Подібно до випадку обчислення похідних пакет в якості меж інтегрування, а також констант і змінних підінтегрального виразу, допускає використання ранжованих змінних, що дає можливість виводити результати обчислення інтеграла у вигляді вихідних таблиць. Дана можливість дозволяє отримувати досить точні графіки первісних функцій. Поряд з однократними пакет дозволяє обчислювати також m-кратні інтеграли, для чого в конструкцію вводяться підряд знаки інтеграла за числом (m) кратності інтеграла, що обчислюється. Але до m-кратних інтегралів потрібно звертатися тільки у випадку крайньої необхідності, тому що з ростом кратності різко зростає час їх обчислення. Комплексні числа Комплексне число задається в алгебраїчній формі як Комплексне спряження виводиться символом подвійних лапок після набрання імені змінної ( Для роботи з комплексними числами пакет має такі функції: 1. Re(z) – дійсна частина числа; 2. Im(z) – уявна частина числа; 3. arg(z) – аргумент (кут в комплексній площині між додатнім напрямом осі ох і z); 4. 5. csgn(z) – повертає або 0, якщо 6. signum(z) –повертає 0, якщо Розв’язок задачі Коші При розв’язуванні диференціального рівняння шуканою величиною є функція. MathCAD має ряд вбудованих функцій, призначених для чисельного розв’язання диференціального рівняння. В результаті розв’язання одержується матриця, яка містить значення функції–розв’язку, обчислені на деякій множині точок. При використанні вбудованих функцій, які передбачають різні методи пошуку розв’язку в загальному випадку повинні бути задані такими величинами: 1. Початкові умови; 2. Набір точок, в яких потрібно знайти розв’язок; 3. Саме диференціальне рівняння. Для розв’язання диференціальних рівнянь першого порядку в MathCAD використовується функція rkfixed(y,x1,x2,n,D), яка використовує метод Рунге-Кутта 4-го порядку. y – вектор початкових умов розмірності n, де n – порядок диференціального рівняння чи кількість рівнянь у системі. У випадку диференціального рівняння першого порядку вектор початкових умових вироджується в одну точку x1, x2 – граничні точки інтервалу, на якому шукається розв’язок диференціального рівняння. n – кількість точок (не рахуючи початкової), в яких шукається наближений розв’язок. Цей аргумент визначає кількість рядків (n+1) в матриці, яку повертає функція rkfixed. D(x,y) – вектор-функція перших похідних. О.М.Дудка
АВТОМАТИЗАЦІЯ МАТЕМАТИЧНИХ РОЗРАХУНКІВ ЗАСОБАМИ ПАКЕТУ MathCAD Навчальний посібник Є доп. видання
Івано-Франківськ -2004- ВСТУП Широке впровадження електронно-обчислювальної техніки в найрізноманітніших галузях людської діяльності поставило на порядок денний вимогу, щоб фахівець будь-якої професії вмів використовувати нові інформаційні технології в своїй практичній діяльності. Впровадження в навчальний процес сучасних засобів збирання, зберігання, опрацювання, подання, передавання інформації відкриває широкі перспективи щодо гуманітаризації освіти і гуманізації навчального процесу, поглиблення та розширення теоретичної бази знань і надання результатам навчання практичного значення, активізації пізнавальної діяльності, створення умов для повного розкриття творчого потенціалу людини з урахуванням її вікових особливостей і життєвого досвіду, індивідуальних нахилів, запитів і здібностей. На сьогодні розроблено значну кількість програмних засобів, що дозволяють розв'язувати за допомогою комп'ютера досить широке коло математичних задач різних рівнів складності. Причому одні з цих програм розраховані на фахівців досить високої кваліфікації в галузі математики, інші - на учнів середніх навчальних закладів чи студентів вузів, які лише почали вивчати шкільний курс математики чи основи вищої математики. Серед цих програм такі як DERIVE, EUREKA, GRAN1, Maple, Mathematika, MathLab, Maxima, Numeri, Reduce, Statgraph, MathCA. Використання програм дає можливість розв'язувати окремі задачі, не знаючи відповідного аналітичного апарату, методів і формул, правил перетворення виразів тощо. Використання подібних програм дає можливість у багатьох випадках зробити розв'язування задач настільки ж доступними, як і просте розглядання малюнків чи графічних зображень. Відповідні програми перетворюють окремі розділи і методи математики в «математику для всіх», що робить їх доступними, зрозумілими, легкими і зручними для використання, а той, хто розв'язує задачу, стає користувачем математичних методів, можливо не володіючи їхньою будовою і обгрунтуванням, аналогічно до того, як він використовує інші комп'ютерні програми (текстові, графічні, музичні редактори, електронні таблиці, бази даних, операційні оболонки, експертні системи), не знаючи, як і за якими принципами вони побудовані, якими мовами програмування описані, які теоретичні положення покладено в їхню основу. З іншого боку, такий підхід до вивчення математики дає наочні уявлення про поняття, що вивчаються, розвиває образне мислення, просторову уяву, дозволяє досить глибоко проникнути в сутність досліджуваного явища, неформально розв'язувати задачу. При цьому на передній план виступає з'ясування проблеми, постановка задачі, розробка відповідної математичної моделі, матеріальна інтерпретація отриманих за допомогою комп'ютера результатів. Усі технічні операції щодо опрацювання побудованої математичної моделі, реалізації методу відшукання розв'язку, оформлення та подання результатів опрацювання вхідної інформації покладаються на комп'ютер. Важко переоцінити ефективність використання програм зазначеного типу і в разі поглибленого вивчення математики. Можливість провести необхідний чисельний експеримент, швидко виконати потрібні обчислення чи графічні побудови, перевірити ту чи іншу гіпотезу, випробувати той чи інший метод розв'язування задачі, вміти проаналізувати та пояснити результати, отримані за допомогою комп'ютера, з'ясувати межі можливостей застосування комп'ютера чи обраного методу розв'язування задачі має надзвичайне значення у вивченні математики. Розглянемо зокрема пакет MathCAD for Windows(Mathematical Computer Aided Design – математичне автоматизоване проектування) фірми Mathsoft Inc. Пакет MathCAD є унікальною системою для роботиз числами, формулами, текстами і графіками. Пакет є гнучкий та надійний, цікавий для вивчення та достатньо простий у користуванні. Він надає користувачу одночасно можливості електронної таблиці і текстового процесора. Як у електронних таблицях будь-яка зміна вмісту робочого документу MathCAD for Windows викликає поновлення, перерахунок всіх залежних результатів, в тому числі і перерисовку графіків. Дозволяє читати дані із файлів і виконувати над ними довільні математичні перетворення. Подібно до текстового процесора MathCAD for Windows має інтерфейс wysiwyg (What You See Is What You Get – що ви бачите, те і одержите), множину різних шрифтів і можливість друкувати те, що зображено на екрані дисплея, на будь-якому принтері, робота якого підтримується системою Windows. MathCAD – не тільки засіб для вирішення різного роду математичних задач. Це, по суті, потужна математична САПР (система автоматизованого проектування), яка дозволяє готувати на найвищому поліграфічному рівні любі матеріали, які відносяться до науки і техніки: документацію, наукові звіти, книги і статті, дисертації, дипломні і курсові проекти. При цьому в них одночасно можуть бути складні тексти, різні математичні формули, складні обчислення, графіки функцій і ілюстративні матеріали. Пакет дозволяє готувати високоякісні електронні книги з гіпертекстовими посиланнями. Даний навчальний посібник побудовано як конспект лекцій з лабораторними роботами для методичного забезпечення курсу “Автоматизація математичних розрахунків”, який би сприяв закріпленню теоретичного матеріалу і розвитку практичних навиків при розв’язанні різноманітних математичних задач не тільки шкільного курсу, а й при розв’язуванні задач, які вимагають досить високої кваліфікації в галузі математики, зокрема таких як “Математичний аналіз” – знаходження інтегралів і диференціалів, обчислення сум рядів, “Алгебра” – перетворення, транспонування, обчислення визначників і матриць, “Елементарна математика” – розклад виразів на множники і зведення до найпростішого виду, розв’язування рівнянь і нерівностей, побудова графіків та ін. Даний матеріал може бути використаний викладачами і студентами технічних, математичних, економічних, фізичних спеціальностей інститутів та університетів. Розділ 1. Пакет MathCAD як засіб автоматизації математичних розрахунків
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.21.68 (0.016 с.) |

 при різних значеннях аргументів. Для цього означимо цей вираз як функцію користувача, наприклад,
при різних значеннях аргументів. Для цього означимо цей вираз як функцію користувача, наприклад,  :
: 
 обчислюємо її при необхідних значеннях аргументів, чи проводимо будь-які інші математичні операції.
обчислюємо її при необхідних значеннях аргументів, чи проводимо будь-які інші математичні операції.


 , де
, де  – дійсна частина комплексного числа
– дійсна частина комплексного числа  , і
, і  – уявна частина
– уявна частина  , комплексне число
, комплексне число  , – як уявне. Значення
, – як уявне. Значення  задається в полосі зі щотчиком Поріг для комплексних чисел (Сomplex Threshold) на закладці Допуск (Tolerance).
задається в полосі зі щотчиком Поріг для комплексних чисел (Сomplex Threshold) на закладці Допуск (Tolerance).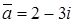 ).
). – модуль
– модуль  ;
; , або 1, якщо
, або 1, якщо  , або якщо
, або якщо 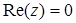 і
і  , або – 1 в інших випадках;
, або – 1 в інших випадках; в іншому випадку.
в іншому випадку. .
.


