
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Символьні операції перетвореньСодержание книги Поиск на нашем сайте
Фурьє – виконати пряме перетворення Фурьє відносно виділеної змінної; Фурьє Зворотнє – виконати обернене перетворення Фурьє відносно виділеної змінної; Лапласа - виконати пряме перетворення Лапласа відносно виділеної змінної; Лапласа Зворотне - виконати обернене перетворення Лапласа відносно виділеної змінної. Обчислення похідних та інтегралів в середовищі Пакету MathCAD. Комплексні числа Обчислення похідних В середовищі пакету відбувається як символьне так і чисельне обчислення значень m-кратних похідних (m>1) і частинних похідних функцій у заданих точках. Для здійснення операції диференціювання потрібно натиснути клавішу знака запитання “?”, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку похідної. В результаті на екрані генерується знак операції з двома покажчиками:
Покажчик, що стоїть в знаменнику, вимагає означення змінної диференціювання, тоді як активний покажчик – функцію (її вираз чи ім’я), що диференціюється. Змінна диференціювання і всі константи та змінні, що входять у функцію повинні бути попередньо означені. Знак операції похідної вищого порядку може бути генерований кількаразовим натиском клавіші “?” по необхідності, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку Похідна N-го порядку. В результаті на екрані генерується знак операції з чотирма покажчиками:
В якості змінних диференціювання, констант і змінних диференційованої функції можуть виступати і ранжовані змінні. Дана можливість пакету дозволяє, наприклад, виводити графік похідної будь-якої плоскої функції або частинної похідної в заданій січній площині.
Обчислення інтегралів Пакет дозволяє символьно та чисельно обчислювати як звичайні, так і криволінійні інтеграли, крім того, серед них – багато інтегралів, підінтегральні функції яких мають особливості на кінцях відрізка інтегрування. Для вводу знаку операції інтегрування потрібно натиснути клавішу “&”, або вибрати в панелі інструментів Математика кнопку Матаналіз та кнопку Визначений інтеграл. В результаті на екрані з’явиться знак операції з чотирма покажчиками:
Для означення і обчислення інтеграла необхідно замість активного покажчика задати підінтегральну функцію, після знака диференціала (d) потрібно означити змінну інтегрування, а замість покажчиків, що є знизу і зверху знаку інтеграла, вказати дійсні вирази, які визначають відповідно значення нижньої і верхньої меж інтегрування.
В якості меж інтегрування повинні бути тільки дійсні вирази, тоді як підінтегральна функція може бути як дійсною, так і комплексною. Крім змінної інтегрування (ім’я якої повинне задовольняти умови пакету), інші змінні і константи, які використовуються в конструкції, повинні бути попередньо означені. Подібно до випадку обчислення похідних пакет в якості меж інтегрування, а також констант і змінних підінтегрального виразу, допускає використання ранжованих змінних, що дає можливість виводити результати обчислення інтеграла у вигляді вихідних таблиць. Дана можливість дозволяє отримувати досить точні графіки первісних функцій. Поряд з однократними пакет дозволяє обчислювати також m-кратні інтеграли, для чого в конструкцію вводяться підряд знаки інтеграла за числом (m) кратності інтеграла, що обчислюється. Але до m-кратних інтегралів потрібно звертатися тільки у випадку крайньої необхідності, тому що з ростом кратності різко зростає час їх обчислення. Комплексні числа Комплексне число задається в алгебраїчній формі як Комплексне спряження виводиться символом подвійних лапок після набрання імені змінної ( Для роботи з комплексними числами пакет має такі функції: 1. Re(z) – дійсна частина числа; 2. Im(z) – уявна частина числа; 3. arg(z) – аргумент (кут в комплексній площині між додатнім напрямом осі ох і z); 4. 5. csgn(z) – повертає або 0, якщо 6. signum(z) –повертає 0, якщо
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.218.107 (0.009 с.) |




 , де
, де  – дійсна частина комплексного числа
– дійсна частина комплексного числа  , і
, і  – уявна частина
– уявна частина  , комплексне число
, комплексне число  , – як уявне. Значення
, – як уявне. Значення  задається в полосі зі щотчиком Поріг для комплексних чисел (Сomplex Threshold) на закладці Допуск (Tolerance).
задається в полосі зі щотчиком Поріг для комплексних чисел (Сomplex Threshold) на закладці Допуск (Tolerance).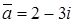 ).
). – модуль
– модуль  ;
; , або 1, якщо
, або 1, якщо  , або якщо
, або якщо 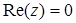 і
і  , або – 1 в інших випадках;
, або – 1 в інших випадках; в іншому випадку.
в іншому випадку.


