
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1. Основы работы с MathcadСодержание книги
Поиск на нашем сайте
Лабораторная работа 1. Основы работы с Mathcad
MathCAD работает с документами. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области. Расположение нетекстовых блоков в документе имеет принципиальное значение - слева направо и сверху вниз.
Математические выражения
К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры. Операторы Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д. Оператор определяет: 1. действие, которое должно выполняться при наличии тех или иных значений операндов; 2. сколько, где и какие операнды должны быть введены в оператор. Операнд - число или выражение, на которое действует оператор. Например, в выражении 5! + 3 число 3 и выражение 5! - операнды оператора + (плюс), а число 5 операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками. В Приложении 2 данного пособия приведен список наиболее часто используемых операторов. Типы данных К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа. Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.
В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения (см. Приложение 1). Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика Þ Опции.
Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной. Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши: (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака
Рисунок 1.
MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания ( Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства ® (комбинация клавиш Ctrl +.). Дискретные аргументы - особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного (2 способ). 1. Name:= Nbegin.. Nend, где Name - имя переменной, Nbegin - ее начальное значение, Nend - конечное значение, .. - символ, указывающий на изменение переменной в заданных пределах (вводится клавишей;). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе -1. 2. Name:= Nbegin, (Nbegin + Step).. Nend Здесь Step - заданный шаг изменения переменной (он должен быть положительным, если Nbegin < Nend, или отрицательным в обратном случае). Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы (Пример 3 Рисунка 1).
Массив - имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов: · одномерные (векторы); · двумерные (матрицы). Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN (см. Приложение 1). Векторы и матрицы можно задавать различными способами: · с помощью команды Вставка Þ Матрица, или комбинации клавиш Ctrl + M, или щелчком на кнопке · с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов через их индексы (Пример 3 Рисунка 1). Функции Функция - выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется его числовое значение. Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции (см. Пример 2 Рисунка 1). Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение. Функции в пакете MathCAD могут быть встроенные (см. Приложение 3), т. е. заблаговременно введенные разработчиками, и определенные пользователем. Способы вставки встроенной функции: 1. Выбрать пункт меню Вставка Þ Функция. 2. Нажать комбинацию клавиш Ctrl + E. 3. Щелкнуть на кнопке
Текстовые фрагменты
Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов: · текстовая область предназначена для небольших кусков текста - подписей, комментариев и т. п. Вставляется с помощью команды Вставка Þ Текстовая регион или комбинации клавиш Shift + " (двойная кавычка); · · текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift + Enter.
Графические области
Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим MathCAD на основании обработанных данных. Для создания декартового графика: 1. Установить визир в пустом месте рабочего документа. 2. Выбрать команду Вставка Þ График Þ Х-У график, или нажать комбинацию клавиш Shift + @, или щелкнуть кнопку 3. Введите в средней метке под осью Х первую независимую переменную, через запятую - вторую и так до 10, например х 1, х 2, … 4. Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую - вторую и т. д., например у 1(х 1), у 2(х 2), …, или соответствующие выражения.
5. Щелкните за пределами области графика, что бы начать его построение. Трехмерные, или 3D-графики, отображают функции двух переменных вида Z (X, Y). При построении трехмерных графиков в ранних версиях MathCAD поверхность нужно было определить математически (Рисунок 2, способ 2). Теперь применяют функцию MathCAD CreateMesh.
Рисунок 2.
CreateMesh(F (или G, или f 1, f 2, f 3), x 0, x 1, y 0, y 1, xgrid, ygrid, fmap) Создает сетку на поверхности, определенной функцией F. x 0, x 1, y 0, y 1- диапазон изменения переменных, xgrid, ygrid - размеры сетки переменных, fmap - функция отображения. Все параметры, за исключением F, - факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от -5 до 5 и с сеткой 20*20 точек. Пример использования функции CreateMesh для построения 3D-графиков приведен на Рисунке 2, способ 1. На Рисунке 2 построена одна и та же поверхность разными способами, с разным форматированием, причем изображены поверхности и под ними те же поверхности в виде контурного графика. Такое построение способно придать рисунку большую наглядность.
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка Þ График Þ 3D Точечный, причем поверхность задается параметрически - с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2.
Рисунок 3.
Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1). CreateSpace (F, t 0, t 1, tgrid, fmap) Возвращает вложенный массив трех векторов, представляющих х -, у -, и z -координаты пространственной кривой, определенной функцией F. t 0 и t 1 - диапазон изменения переменной, tgrid - размер сетки переменной, fmap - функция отображения. Все параметры, за исключением F, - факультативные. Рисунок 4.
Рисунок 5.
root(f (х 1, x 2, …), х 1, a, b) Возвращает значение х 1, принадлежащее отрезку [ a, b ], при котором выражение или функция f (х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. Аргументы: f (х 1, x 2, …) -функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения. х 1 -- имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
a, b -необязательны, если используются, то должны быть вещественными числами, причем a < b. Приближенные значения корней (начальные приближения) могут быть: 1. Известны из физического смысла задачи. 2. Известны из решения аналогичной задачи при других исходных данных. 3. Найдены графическим способом. Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравнения f (x) = 0 - это точки пересечения графика функции f (x) с осью абсцисс, достаточно построить график функции f (x) и отметить точки пересечения f (x)с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение f (x) = 0 равносильным ему уравнением:
где функции f 1(x) и f 2(x) - более простые, чем функция f (x). Тогда, построив графики функций у = f 1(x) и у = f 2(x), искомые корни получим как абсциссы точек пересечения этих графиков. Пример. Графически отделить корни уравнения:
Уравнение (1) удобно переписать в виде равенства: lg x= Отсюда ясно, что корни уравнения (1) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = Рекомендации по использованию функции root · Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида · Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их. · Если функция f (x) имеет малый наклон около искомого корня, функция root (f (x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f (x) = 0на g (x) = 0
· Для выражения f (x) с известным корнем а нахождение дополнительных корней f (x) эквивалентно поиску корней уравнения h (x) = f (x)/(x - a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h (x), чем пробовать искать другой корень уравнения f (x) = 0, выбирая различные начальные приближения.
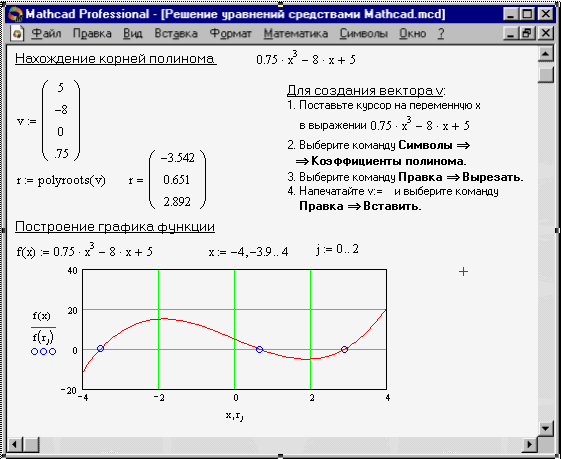
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид vnxn +... + v 2 x 2 + v 1 x + v 0, лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Polyroots(v) Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома.
Аргументы: v -вектор, содержащий коэффициенты полинома. Вектор v удобно создавать использую команду Символы Þ Коэффициенты полинома. Рисунок 6 иллюстрирует определение корней полинома средствами Mathcad.
Рисунок 6.
Решение систем уравнений MathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня. Для решения системы уравнений необходимо выполнить следующее: · Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов. · Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. · Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, · Введите любое выражение, которое включает функцию Find, например: а:= Find (х, у). Find (z 1, z 2 ,...) Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блокомрешенияуравнений. Следующие выражения недопустимы внутри блока решения: · Ограничения со знаком · Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме. · Неравенства вида a < b < c. Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find. Функция, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции. Можно произвести с ней следующие три действия: · Можно вывести найденное решение, напечатав выражение вида: Find (var 1, var 2,…) =. · Определить переменную с помощью функции Find: a:= Find (x) - скаляр, var:= Find (var 1, var 2,…) - вектор. Это удобно сделать, если требуется использовать решение системы уравнений в другом месте рабочего документа. · Определить другую функцию с помощью Find f (a, b, c, …):= Find (x, y, z, …). Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений. Сообщение об ошибке · Поставленная задача может не иметь решения. · Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот. · В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения. · Возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL. Пример 1 Рисунка 7 иллюстрирует решение системы уравнений в MathCAD.
Рисунок 7.
Решение матричных уравнений Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х 1, х 2, …, хn:
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде
где:
Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы. Если матрица А - неособенная, то есть det A В самом деле, при условии det A
Формула (5) дает решение уравнения (3) и оно единственно. Системы линейных уравнений удобно решать с помощью функции lsolve. lsolve(А, b) Возвращается вектор решения x такой, что Ах = b. Аргументы: А - квадратная, не сингулярная матрица. b - вектор, имеющий столько же рядов, сколько рядов в матрице А. На Рисунке 8 показано решение системы трех линейных уравнений относительно трех неизвестных.
Рисунок 8.
Приближенные решения Функция Minerr очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find. Minerr(z 1, z 2 ,...) Возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Если Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.
Символьное решение уравнений
В Mathcad можно быстро и точно найти численное значение корня с помощью функции root. Но имеются некоторые задачи, для которых возможности Mathcad позволяют находить решения в символьном (аналитическом) виде. Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения: · Если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении. · Если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде. Команда Символы Þ Переменные Þ Вычислить позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения. Чтобы решить уравнение символьно необходимо: · Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш [Ctrl]=). · Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью. · Выбрать пункт меню Символы Þ Переменные Þ Вычислить. Нет необходимости приравнивать выражение нулю. Если MathCAD не находит знака равенства, он предполагает, что требуется приравнять выражение нулю. Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее: · Напечатать ключевое слово Given. · Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака = используется [Ctrl]=. · Напечатать функцию Find, соответствующую системе уравнений. · Нажать [Ctrl]. (клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства ®. · Щелкнуть мышью на функции Find. Пример 2 Рисунка 7 иллюстрирует символьное решение системы уравнений в MathCAD. Рисунок 9.
Примеры символьных операций в командном режиме
Большинство символьных операций легко выполняются, так что ниже мы остановимся лишь на некоторых примерах. Символьная операция Расчеты обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. (Рисунок 10).
Рисунок 10.
Операция стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме. Особо следует отметить возможность выполнения численных вычислений с повышенной точностью - 20 знаков после запятой. Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа. На Рисунке 10 показаны типовые примеры действия операции Расчеты. Здесь слева показаны исходные выражения, подвергаемые символьным преобразованиям, а справа - результат этих преобразований. Операция Расчеты одна из самых мощных. Как видно из Рисунка 6, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами. Эта операция содержит подменю. Команда Символические тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа p получить 3.141..., используйте команду С плавающей запятой…. В режиме символьных вычислений результат может превосходить машинную бесконечность системы - см. пример на вычисление ехр(1000.0) на Рисунке 10. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ). Операция Разложить на составляющие... возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п = 6. В разложении указывается остаточная погрешность разложения. На Рисунке 11 представлено применение этой операции для разложения функции
Рисунок 11.
Операторы вычисления пределов функций
Для вычисления пределов функций в систему введен символьный оператор limit. Помимо ввода с наборной панели Матанализ, его в трех формах можно ввести нажатием следующих комбинаций клавиш: [ Ctrl ] L - ввод шаблона оператора вычисления предела функции при х, стремящемся к заданному значению, [ Ctrl ] A - ввод шаблона вычисления предела функции слева от заданной точки, [ Ctrl ] B - ввод шаблона вычисления предела функции справа от заданной точки. На Рисунке 12 показаны примеры вычисления пределов. При вычислении пределов нужно заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной - аргумента функции.
Рисунок 12.
Для получения результата установите после блока вычисления предела стрелку с острием, направленным вправо. Предел (если он существует) будет вычислен и появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо результата появится надпись Undefine.
Задание операторов пользователя
Еще одна экзотическая возможность, присущая новым версиям системы MathCAD, - задание новых операторов пользователя. Такой оператор задается практически так же, как функция пользователя, но вместо имени выбирается какой-либо подходящий знак. Например, можно задать оператор деления в виде:
При кажущейся простоте такого задания здесь есть проблемы. Встроенные в систему операторы нельзя переопределить. Поэтому набор доступных знаков для обозначения новых операторов ограничен. Нельзя задать новый оператор деления знаком / (он уже использован), но можно взять знак Вторая проблема связана с вводом символа нового оператора. Скорее всего, его напрямую ввести нельзя. Придется воспользоваться типовыми приемами ввода новых символов в документы Windows. Один из этих приемов - использование приложения, выдающего таблицу символов, с возможностью его экспорта из этой таблицы в документ другого приложения (в нашем случае - в документ MathCAD). Можно также воспользоваться подходящим знаком из набора MATH SYMBOL, имеющегося в составе Шпаргалок, доступ к которым дает Ресурс Центр (Ресурс Центр Þ Справочный стол и краткое руководство Þ Дополнительные математические символы). На Рисунке 8 показан такой вариант задания нового оператора пользователя. Для перетаскивания знака можно скопировать его в буфер обмена с помощью операции Копировать, а затем ввести в документ, используя операцию Вставка. После того как оператор задан, его можно использовать, как функцию и как оператор. Примеры показаны на Рисунке 13.
Рисунок 13.
Для применения нового оператора надо вывести его шаблон с помощью панели математических знаков (она также показана Рисунке 13). В нашем случае следует нажать кнопку Можно задать и другие операторы, например, для работы с одним операндом. Так, вы можете задать оператор для пересчета значения температуры по шкале Цельсия, с тем чтобы определить соответствующее ему значение по шкале Фаренгейта, следующим образом
Затем, используя кнопку
Есть области математики и физики, где задание новых операторов необходимо, поскольку является частью специфического языка их описания.
Лабораторная работа 1. Основы работы с Mathcad
MathCAD работает с документами. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать блоки трех основных типов: математические выражения, текстовые фрагменты и графические области. Расположение нетекстовых блоков в документе имеет принципиальное значение - слева направо и сверху вниз.
Математические выражения
К основным элементам математических выражений MathCAD относятся типы данных, операторы, функции и управляющие структуры. Операторы Операторы - элементы MathCAD, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д. Оператор определяет: 1. действие, которое должно выполняться при наличии тех или иных значений операндов; 2. сколько, где и какие операнды должны быть введены в оператор. Операнд - число или выражение, на которое действует оператор. Например, в выражении 5! + 3 число 3 и выражение 5! - операнды оператора + (плюс), а число 5 операнд оператора факториал (!). После указания операндов операторы становятся исполняемыми по документу блоками. В Приложении 2 данного пособия приведен список наиболее часто используемых операторов. Типы данных К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа. Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т. д. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в MathCAD представляют собой набор латинских или греческих букв и цифр.
В MathCAD содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения (см. Приложение 1). Изменение значений системных переменных производят во вкладке Встроенные переменные диалогового окна Math Options команды Математика Þ Опции. Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак :=, тогда как знак = отведен для вывода значения константы или переменной. Если переменной присваивается начальное значение с помощью оператора :=, вызывается нажатием клавиши: (двоеточие) на клавиатуре, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака
Рисунок 1.
MathCAD прочитывает весь документ дважды слева направо и сверху вниз. При первом проходе выполняются все действия, предписанные локальным оператором присваивания ( Существуют также жирный знак равенства = (комбинация клавиш Ctrl + =), который используется, например, как оператор приближенного равенства при решении систем уравнений, и символьный знак равенства ® (комбинация клавиш Ctrl +.). Дискретные аргументы - особый класс переменных, который в пакете MathCAD зачастую заменяет управляющие структуры, назыв
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.141.142 (0.015 с.) |

 (клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1).
(клавиша ~ на клавиатуре) можно обеспечить глобальное присваивание (см. Пример 1 Рисунка 1).
 панели Матрица, заполнив массив пустых полей для не слишком больших массивов;
панели Матрица, заполнив массив пустых полей для не слишком больших массивов;
 панели Графики. Появится шаблон декартового графика.
панели Графики. Появится шаблон декартового графика.

 ,
,

 .
. уравнения (1) или определим его содержащий отрезок [2, 3].
уравнения (1) или определим его содержащий отрезок [2, 3]. . Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Þ Параметры… Þ Переменные Þ Допуск сходимости (TOL).
. Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика Þ Параметры… Þ Переменные Þ Допуск сходимости (TOL). .
.
 и
и 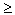 .
. .
. (Решение не найдено) при решении уравнений появляется, когда:
(Решение не найдено) при решении уравнений появляется, когда: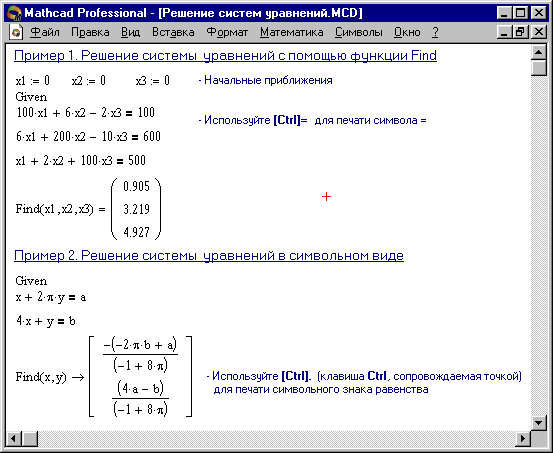


 .
.



 . Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).
. Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).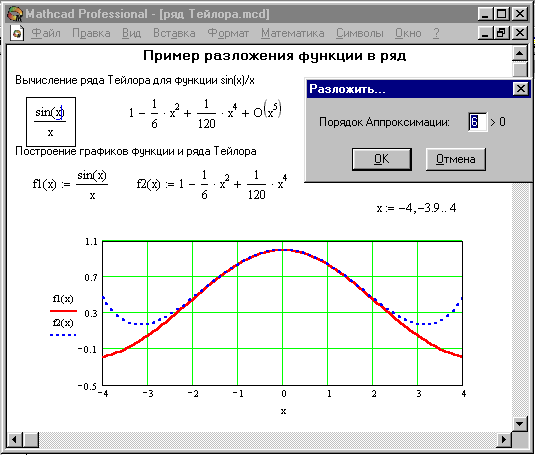

 - задание нового оператора деления;
- задание нового оператора деления;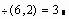 - применение функции деления;
- применение функции деления; - применение нового оператора деления.
- применение нового оператора деления. , поскольку этот символ системой не используется.
, поскольку этот символ системой не используется.
 этой панели - она выводит особый шаблон вида § § §. Введите операнды, например 6 и 3 в крайние прямоугольники, а символ оператора - в средний. Поставив после этой конструкции знак равенства, увидите результат - число 2.
этой панели - она выводит особый шаблон вида § § §. Введите операнды, например 6 и 3 в крайние прямоугольники, а символ оператора - в средний. Поставив после этой конструкции знак равенства, увидите результат - число 2.
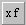 наборной панели символов отношения, можно выполнять операцию пересчета в виде.
наборной панели символов отношения, можно выполнять операцию пересчета в виде.



