
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции с выделенными переменнымиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для ряда операций надо знать, относительно какой переменной они выполняются. В этом случае необходимо выделить переменную, установив на ней маркер ввода. После этого становятся доступными следующие операции подменю Переменные: Вычислить - найти значения выделенной переменной, при которых содержащее ее выражение становится равным нулю; Замена - заменить указанную переменную содержимым буфера обмена; Дифференциалы - дифференцировать выражение, содержащее выделенную переменную, по этой переменной (остальные переменные рассматриваются как константы); Интеграция - интегрировать все выражение, содержащее переменную, по этой переменной; Разложить на составляющие... - найти несколько членов разложения выражения в ряд Тейлора относительно выделенной переменной; Преобразование в Частичные Доли - разложить на элементарные дроби выражение, которое рассматривается как рациональная дробь относительно выделенной переменной. Операции с выделенными матрицами Операции с выделенными матрицами представлены позицией подменю Матрицы, которая имеет свое подменю со следующими операциями: Транспонирование - получить транспонированную матрицу; Инвертирование - создать обратную матрицу; Определитель - вычислить детерминант (определитель) матрицы. Результаты символьных операций с матрицами часто оказываются чрезмерно громоздкими и поэтому плохо обозримы. Операции преобразования В позиции Преобразование содержится раздел операций преобразования, создающий подменю со следующими возможностями: Фурье - выполнить прямое преобразование Фурье относительно выделенной переменной; Фурье Обратное - выполнить обратное преобразование Фурье относительно выделенной переменной; Лапласа - выполнить прямое преобразование Лапласа относительно выделенной переменной (результат - функция переменной s); Лапласа Обратное - выполнить обратное преобразование Лапласа относительно выделенной переменной (результат - функция переменной t); Z - выполнить прямое Z-преобразование выражения относительно выделенной переменной (результат - функция переменной z); Обратное Z - выполнить обратное Z-преобразование относительно выделенной переменной (результат - функция переменной n).
Стиль представления результатов вычислений
На наглядность вычислений влияет стиль представления их результатов. Следующая команда позволяет задать тот или иной стиль: Стиль Вычислений... - задать вывод результата символьной операции под основным выражением, рядом с ним или вместо него (Рисунок 9).
Рисунок 9.
Примеры символьных операций в командном режиме
Большинство символьных операций легко выполняются, так что ниже мы остановимся лишь на некоторых примерах. Символьная операция Расчеты обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. (Рисунок 10).
Рисунок 10.
Операция стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме. Особо следует отметить возможность выполнения численных вычислений с повышенной точностью - 20 знаков после запятой. Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа. На Рисунке 10 показаны типовые примеры действия операции Расчеты. Здесь слева показаны исходные выражения, подвергаемые символьным преобразованиям, а справа - результат этих преобразований. Операция Расчеты одна из самых мощных. Как видно из Рисунка 6, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами. Эта операция содержит подменю. Команда Символические тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа p получить 3.141..., используйте команду С плавающей запятой…. В режиме символьных вычислений результат может превосходить машинную бесконечность системы - см. пример на вычисление ехр(1000.0) на Рисунке 10. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ).
Операция Разложить на составляющие... возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п = 6. В разложении указывается остаточная погрешность разложения. На Рисунке 11 представлено применение этой операции для разложения функции
Рисунок 11.
Операторы вычисления пределов функций
Для вычисления пределов функций в систему введен символьный оператор limit. Помимо ввода с наборной панели Матанализ, его в трех формах можно ввести нажатием следующих комбинаций клавиш: [ Ctrl ] L - ввод шаблона оператора вычисления предела функции при х, стремящемся к заданному значению, [ Ctrl ] A - ввод шаблона вычисления предела функции слева от заданной точки, [ Ctrl ] B - ввод шаблона вычисления предела функции справа от заданной точки. На Рисунке 12 показаны примеры вычисления пределов. При вычислении пределов нужно заполнить шаблоны, входящие в главный шаблон для вычисления пределов, а затем ввести функцию, имя переменной, по которой ищется предел, и значение переменной - аргумента функции.
Рисунок 12.
Для получения результата установите после блока вычисления предела стрелку с острием, направленным вправо. Предел (если он существует) будет вычислен и появится в шаблоне у острия стрелки. Если функция не имеет предела, вместо результата появится надпись Undefine.
Задание операторов пользователя
Еще одна экзотическая возможность, присущая новым версиям системы MathCAD, - задание новых операторов пользователя. Такой оператор задается практически так же, как функция пользователя, но вместо имени выбирается какой-либо подходящий знак. Например, можно задать оператор деления в виде:
При кажущейся простоте такого задания здесь есть проблемы. Встроенные в систему операторы нельзя переопределить. Поэтому набор доступных знаков для обозначения новых операторов ограничен. Нельзя задать новый оператор деления знаком / (он уже использован), но можно взять знак Вторая проблема связана с вводом символа нового оператора. Скорее всего, его напрямую ввести нельзя. Придется воспользоваться типовыми приемами ввода новых символов в документы Windows. Один из этих приемов - использование приложения, выдающего таблицу символов, с возможностью его экспорта из этой таблицы в документ другого приложения (в нашем случае - в документ MathCAD). Можно также воспользоваться подходящим знаком из набора MATH SYMBOL, имеющегося в составе Шпаргалок, доступ к которым дает Ресурс Центр (Ресурс Центр Þ Справочный стол и краткое руководство Þ Дополнительные математические символы). На Рисунке 8 показан такой вариант задания нового оператора пользователя. Для перетаскивания знака можно скопировать его в буфер обмена с помощью операции Копировать, а затем ввести в документ, используя операцию Вставка.
После того как оператор задан, его можно использовать, как функцию и как оператор. Примеры показаны на Рисунке 13.
Рисунок 13.
Для применения нового оператора надо вывести его шаблон с помощью панели математических знаков (она также показана Рисунке 13). В нашем случае следует нажать кнопку Можно задать и другие операторы, например, для работы с одним операндом. Так, вы можете задать оператор для пересчета значения температуры по шкале Цельсия, с тем чтобы определить соответствующее ему значение по шкале Фаренгейта, следующим образом
Затем, используя кнопку
Есть области математики и физики, где задание новых операторов необходимо, поскольку является частью специфического языка их описания.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.103.114 (0.011 с.) |



 . Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).
. Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).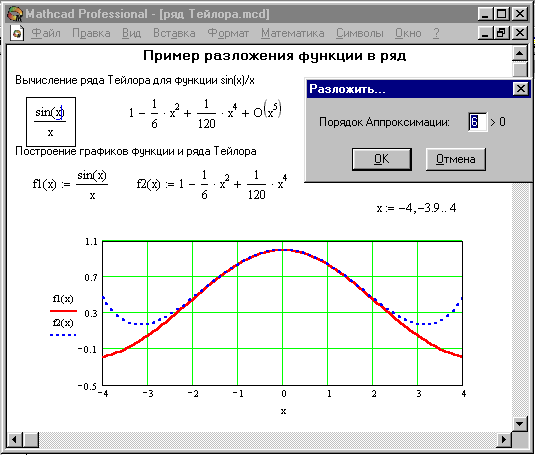

 - задание нового оператора деления;
- задание нового оператора деления;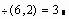 - применение функции деления;
- применение функции деления; - применение нового оператора деления.
- применение нового оператора деления. , поскольку этот символ системой не используется.
, поскольку этот символ системой не используется.
 этой панели - она выводит особый шаблон вида § § §. Введите операнды, например 6 и 3 в крайние прямоугольники, а символ оператора - в средний. Поставив после этой конструкции знак равенства, увидите результат - число 2.
этой панели - она выводит особый шаблон вида § § §. Введите операнды, например 6 и 3 в крайние прямоугольники, а символ оператора - в средний. Поставив после этой конструкции знак равенства, увидите результат - число 2.
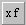 наборной панели символов отношения, можно выполнять операцию пересчета в виде.
наборной панели символов отношения, можно выполнять операцию пересчета в виде.



