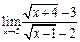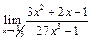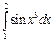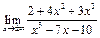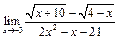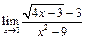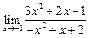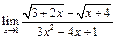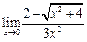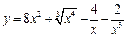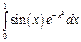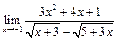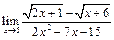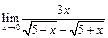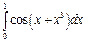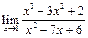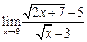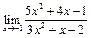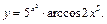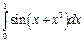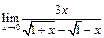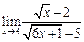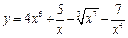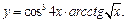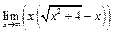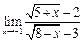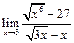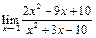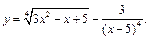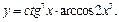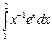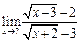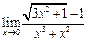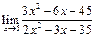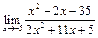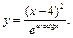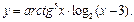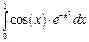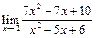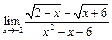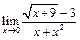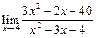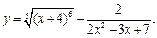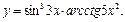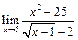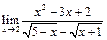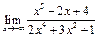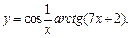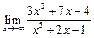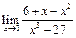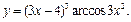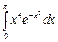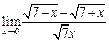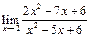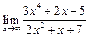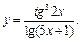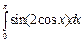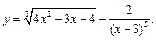Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление пределов, производных и интегралов в пакете MathcadСодержание книги
Поиск на нашем сайте
ЦЕЛЬ. Научиться выполнять вычисления пределов, численных значений производных и определенных интегралов, а также эти вычисление в символьном виде. Основные положения Вычисление пределов Для вычисления пределов, производных и интегралов используется панель Матанализ, которая вызывается кнопкой Для вычисления пределов используется кнопка Пример:
Численное вычисление производных Для определения операции дифференцирования следует нажать клавишу вопроса (“? ”) или кнопку
Можно вычислить производную n-го порядка с помощью кнопки. Все переменные и константы должны быть предварительно определены локально или глобально (или совместно). Дифференцируемая функция может быть как действительной, так и комплексной. Численное вычисление определенных интегралов Для ввода знака операции интеграла следует нажать клавишу (@) или кнопку
Пределы интегрирования — только действительные выражения, тогда как подынтегральная функция может быть и действительной, и комплексной.
Вычисление определенного интеграла при помощи численных методов вычисления Метод прямоугольников Для вычисления приближённого значения определённого интеграла отрезок [ a, b ] делят на n равных частей точками a = x 0< x 1< x 2<…< x n= b, так, что x i+1- x i=(b - a)/ n (i =0.. n -1). Длина каждого отрезка (шаг интегрирования) определяется как h =(b - a)/ n, а точки разбиения (узлы) x 0= a, x 1= x 0+ h, … x n= x n-1+ h. В узлах вычисляются ординаты y 0, y 1, …, y n, т.е. y i= f (x i). На частичных отрезках [ x i; x i+1] строят прямоугольники, высота которых равна значению f (x) в какой-либо точке каждого частичного отрезка (рис.11.1 и 11.2). Произведение f (x i)× h определяет площадь частичного прямоугольника, а сумма таких произведений - площадь ступенчатой фигуры, предстающей собой приближённое значение интеграла.
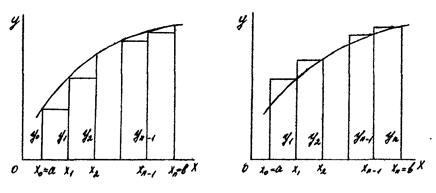
Рис.11.1 Рис.11.2 Если f(xi) вычисляется в левых концах отрезков [xi; xi+1], то получится формула левых прямоугольников:
Если f(xi) вычисляется в правых концах отрезков [xi; xi+1], то получится формула правых прямоугольников:
Для вычисления интеграла I по методу средних прямоугольников функцию f (x i) вычисляют в точках xi +h/2 Î[xi; xi+1]. В результате получают формулу средних прямоугольников
Точность вычисления интеграла зависит от количества прямоугольников, на которые разбивают область интегрирования. Метод трапеций Для вычисления интеграла I по методу трапеций промежуток интегрирования [xn; xk] делят на n равных частей, через точки разбиения проводят прямые параллельно оси y до пересечения с графиком функции f(x) (рис.11.3). Потом соединяют точки пересечения, площади полученных n-криволинейных трапеций заменяют площадями прямоугольных трапеций с высотой h=(xn-x0)/n. Приближенное значение интеграла равно сумме всех площадей частичных трапеций:
где yi=f(xi).
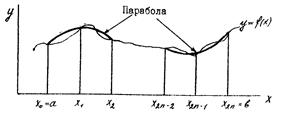
Рис.11.3 Вычисление I по методу трапеций более точное, чем по методу средних прямоугольников. Формула Симпсона Если на частичном отрезке длиной 2h функция f заменяется дугой параболы (рис.11.4), то можно получить формулу парабол или обобщенную формулу Симпсона:
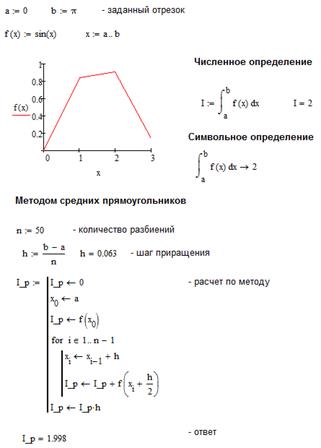
Рис.11.4 Пример расчета определенного интеграла функции в Mathcad методом средних прямоугольников
Задание 1. Выполнить вычисления пределов в среде пакета Mathcad. 2. Выполнить вычисления значения производной и интеграла (вычислить в символьном виде). 3. Реализовать в Mathcad вычисления определенного интеграла с помощью любого численного метода. Примечание. Задания выбрать из таблицы согласно номеру в журнале. Содержание отчета 1) Тема, цель работы. 2) Индивидуальное задание, текст документа Mathcad с результатами вычислений. 3) Составленное задание, текст документа Mathcad с результатами вычислений по заданию 2. 4) Индивидуальное задание, текст документа Mathcad с результатами вычислений по заданию 3. 5) Индивидуальное задание, текст документа Mathcad с результатами вычислений по заданию 4. 6) Выводы по проделанной работе. индивидуальные задания к заданию 1
Контрольные вопросы
1) Какая панель используется для получения символьного расчета пределов, производных и интегралов? 2) Чем отличается символьное решение от численного? 3) Какие заполнители используются при решении численным методом? 4) В чем заключается метод средних прямоугольников? 5) В чем заключается метод трапеций? 6) В чем заключается метод Симпсона? Лабораторная работа № 12 Программирование численных в среде пакета Mathcad ЦЕЛЬ. Изучить численные методы решения уравнений, научиться использовать возможности Mathcad для программирования численных методов. Основные положения В лабораторной работе № 9 мы с вами уже рассматривали решение уравнений в среде пакетаMathcad – графическим методом, с помощью функции root, с помощью решающего блока Given и функции Find. Сегодня мы рассмотрим решение уравнения с помощью численных методов и найдем решение уравнения, создав программы по описанным ниже методам.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.157.5 (0.008 с.) |
.
. Для получения результата используется символический знак равенства, который вызывается кнопкой 
из панели Символы кнопка 
.
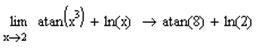
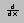, по которой на экране генерируется знак операции с двумя указателями: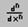
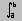, по которой на экране появляется знак операции с 4-мя указателями:
Подынтегральная функция должна быть указана явно, в случае равенства ее константе кодируется данная константа, а не выносится за знак интеграла;
.
.
.
,
.
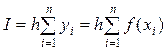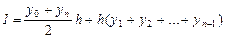