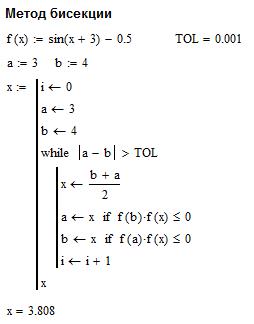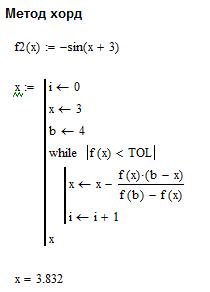Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод половинного деления (бисекции)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Механизм метода бисекции, который больше известен под названием метода половинного деления, очень прост и заключается в том, что полученный при локализации отрезок на каждой итерации делится пополам. Из двух половинок выбирается та, на концах которой функция принимает значения противоположных знаков. То есть проверяется то же условие, что и при методе сканирования. Процесс заканчивается, когда длина полученного интервала становится меньше произведения 2Ɛ. Фактически этот метод исключает возможность появления ошибки. «Аварийная» ситуация может быть вызвана лишь тем, что граница полученного на итерации отрезка попадет в точку разрыва функции. Метод половинного деления наиболее универсальный среди всех итерационных методов. Но, как всегда, бочка меда не обходится без ложки дегтя – для бисекции характерна очень низкая скорость сходимости. Итерационная формула метода бисекции:
Скорость сходимости: низкая Надежность сходимости: высокая Метод Ньютона Задан отрезок [а,b], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(x0)*F"(x0) > 0). В точке F(x0) строится касательная к кривой у = F(x) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Метод Ньютона самый быстрый способ нахождения корней уравнений Итерационная формула имеет вид:
Итерационный процесс проходит до того времени, пока не будет выполнено условие |F(X)|< e, где e - заданная точность.
Рис. 1. Иллюстрация метода Ньютона Рис. 1. иллюстрирует работу метода Ньютона. В данном случае вторая производная функции положительна, поэтому в качестве начального приближения выбрана точка хо = b. Как видно из рисунка, метод имеет очень быструю сходимость среди всех методов решения нелинейных уравнений: обычно заданная точность достигается за 2-3 итерации. Достоинство метода Ньютона: очень быстрая сходимость по сравнению с методом половинного деления и методом простой итерации к заданной точности. Недостаток: громоздкий алгоритм: на каждой итерации необходимо вычислять значение функции и ее первой производной. Метод хорд Для реализации данного метода, нужно построить исходную функцию y=F(x) и найти значения функции на концах отрезка F(a) и F(b). Затем провести хорду М1M2 c концами в точках М1(a, F(a)) и M2(b, F(b)). Абсцисса точки пересечения хорды М1M2 с осью OX это и есть приближенный корень x1. Далее найти точку M3(X1,F(x1)), построить следующую хорду и найти второй приближенный корень x2. И так далее. В зависимости от поведения функции возможны два случая:
Для первого случая (Рис. 1) справедлива следующая формула (8):
и справедливо неравенство: F(a)*F''(a)>0, где x0=b. Для второго случая (Рис. 2) справедлива следующая формула (9):
и справедливо неравенство: F(b)*F''(b)>0, где x0=a. Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона, т. е.:
Метод простых итераций Для нахождения действительных корней уравнения F(x) = 0, где F(x) - непрерывная функция на [a; b], его заменяют равносильным уравнением х = j(х) (14) Это можно сделать всегда, притом не одним способом. Например, уравнение х3 - 9х + 3 = 0 можно представить так:
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня уравнения (14) берут: xn+1 = j(xn), (n = 0, 1, 2,...) (15) Полученная последовательность х0, х1,..., xn, xn+1,... называется итерационной последовательностью, способ построения ее называется методом последовательных приближений или методом итераций численного решения уравнения. При пользовании методом итераций необходимо выяснить основной вопрос: сходится ли полученная последовательность (хn) к решению х* уравнения (14) при возрастании n? Если последовательность (хn) сходится, то есть существует предел
Следовательно, в этом случае х = х* является корнем уравнения х = j(х), а значит, и уравнения F(x) = 0. Если же последовательность (хn) окажется расходящейся, то есть не существует конечного предела построенной последовательности приближений (хn), то это означает, что процесс итераций построен неудачно, и его надо заменить другим. Следовательно, метод последовательных приближений применим при выполнении условия: ½j‘(x)½ £ M1 < 1 (18) для всех х, принадлежащих отрезку изоляции корня уравнения (14), В этом случае процесс итераций сходится, и тем быстрее, чем меньше М1; если же ½j‘(x)½ > 1, то итерационный процесс расходится. Для конкретной оценки величины m1, определяющей скорость сходимости, проще всего пользоваться формулой: М1 = max½j‘(x)½, где max берется по отрезкуизоляции корня [а: b].
Пример решения Mathcad Найти решение уравнения:
Примечание: TOL – системная переменная для задания точности вычислений. Задание 1) Решить уравнение методом бисекции. 2) Решить уравнение методом Ньютона 3) Решить уравнение методом хорд. 4) Решить уравнение методом простой итераций. Содержание отчета 1) Тема, цель работы. 2) Индивидуальное задание, текст документа Mathcad с результатами вычислений по методу бисекции. 3) Индивидуальное задание, текст документа Mathcad с результатами вычислений по методу Ньютона. 4) Индивидуальное задание, текст документа Mathcad с результатами вычислений по методу хорд. 5) Индивидуальное задание, текст документа Mathcad с результатами вычислений по методу простой итерации. 6) Выводы по проделанной работе. индивидуальные задания Таблица 1
Контрольные вопросы 1) В чем суть метода бисекции? 2) В чем суть метода хорд? 3) В чем суть метода Ньютона? 4) В чем суть метода простой итерации? 5) Какие панели и функции Mathcad используются для создания программного расчета?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.199 (0.007 с.) |

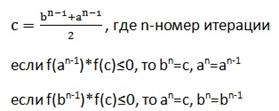

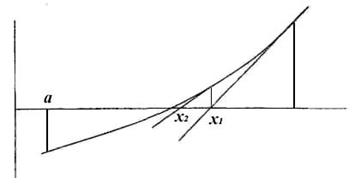
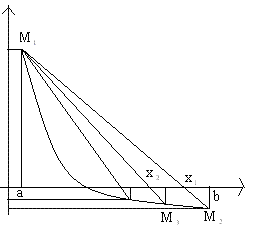 Рис. 1
Рис. 1
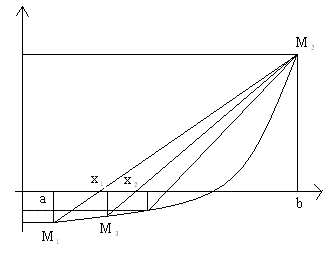 Рис. 2
Рис. 2
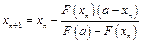
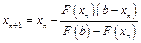
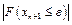

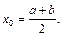 Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы:
Подставляя значение х0 в правую часть уравнения (14), получают первое приближение х1 = j(х0). В качестве второго приближения берут х2 = j(х1). Продолжая этот процесс дальше, получают числовую последовательность (хn), определенную с помощью рекуррентной формулы: то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем:
то, переходя к пределу в равенстве (15) и, предполагая, что функция j(х) непрерывна, получаем: или x* = j(x*). (16)
или x* = j(x*). (16)