
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричная форма записи линейных систем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
Эта система в "свернутом" виде может быть записана в виде
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ах = b, где
Матрица А, столбцами которой являются коэффициенты при соот-ветствующих неизвестных, а строками коэффициенты при неизвест-ных в соответствующем уравнении, называется матрицей системы; Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой искомые неизвестные, называется решением системы. Таким образом, система линейных алгебраических уравнений мо-жет быть записана в матричном виде в виде простейшего матрич-ного уравнения* Ах = b. Если матрица системы невырождена**, то у нее существует обрат-ная матрица и тогда решение системы легко получить, умножив обе части уравнения Ах = b слева на матрицу
Порядок выполнения работы Задание. Решите систему линейных алгебраических уравнений в матричном виде
Указания: 1. Установите режим автоматических вычислений. 2. Введите матрицу системы и матрицу-столбец правых частей. 3. Вычислите решение системы по формуле 4. Проверьте правильность решения умножением матрицы си-стемы на вектор-столбец решения. 5. Найдите решение системы с помощью функции Isolve и срав-ните результаты вычислений. Фрагмент рабочего документа Mathcad, содержащий решение си-стемы, при-веден ниже.
Указание. В приведенном документе для сравнения найдено решение системы с использованием функции решения систем линейных алгебраических уравнений lsolve(A, b) Решите матричное уравнение Ах = b (систему линейных алгебраических уравнений) из индивидуального задания к работе 3. * Матричным уравнением называется уравнение, коэффициенты и неизвестные которого прямоугольные матрицы соответствующей размерности ** Невырожденной называется матрица, определитель которой отличен от нуля.
1. Титульный лист. 2. Решение всех задач с комментариями. Контрольные вопросы
1. К какому типу - прямому или итерационному - относится метод Гаусса? 2. В чем заключается прямой и обратный ход в схеме единственного деления? 3. Как организуется, контроль над вычислениями в прямом и обратном ходе? 4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений? 5. Как формулируется достаточные условия сходимости итерационного процесса? 6. Как эти условия связаны с выбором метрики пространства? 7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации? 8. В чем основное отличие точных и приближенных методов решения систем линейных уравнений? 9. В каких случаях предпочтительны итерационные методы решения систем линейных уравнений? 10. От чего зависит скорость сходимости метода итераций? 11. Каким образом в методе Гаусса можно контролировать накопление вычислительных ошибок? 12. К точным или приближенным методам относится метод Крамера? 13. При каком условии будет сходиться метод итераций? 14. Можно ли заранее оценить число итераций для получения решения с заданной погрешностью? 15. Как влияет вычислительная ошибка на точность решения системы уравнений методом итераций? Литература: 1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича. 2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб.: БХВ-Петербург, 2006. -336 с.: ил. 3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000. 4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с. 5. Ушаков А. Н., Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.35 (0.009 с.) |






 , а поскольку
, а поскольку 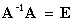 и Ex = x, то
и Ex = x, то  .
.

 Содержание отчета
Содержание отчета
 Лабораторная работа 6
Лабораторная работа 6


