
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные системы с постоянными коэффициентамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система уравнений вида
называется неоднородной системой линейных дифференциальных уравнений с постоянными коэффициентами. Будем считать, что Система дифференциальных уравнений
называется однородной. Вводя в рассмотрение векторы
Матрица
где
...........................
векторного уравнения (2'), называется фундаментальной матрицей этого уравнения. Иногда ее называют матрицей Вронского. Определитель
составленный из частных решений системы (2), называется определителем Вронского. Для того, чтобы матрица (3), где
где C - произвольный постоянный вектор. Общее же решение уравнения (1') будет
где Путем исключения неизвестных систему всегда можно свести к уравнению более высокого порядка с одной неизвестной функцией. Этот метод удобен для решений несложных систем. Пример 1. Решить систему дифференциальных уравнений
Решение. Разрешив первое уравнение относительно y и подставив во второе уравнение системы, получаем
Корни характеристического уравнения
Подставив значение x в первое уравнение системы, найдем
Для решения системы
надо найти корни характеристического уравнения
Каждому простому корню Если для кратного корня Если для корня
Чтобы найти коэффициенты a,b,...,s, надо подставить решение (4) в исходную систему. Приравняв коэффициенты подобных членов в левой и правой части уравнений, получим систему линейных алгебраических уравнений относительно a,b,...,s. Надо найти общее решение этой системы, коэффициенты a,b,...,s должны зависеть от k произвольных постоянных, где k - кратность корня Найдя для каждого Пример 2. Решить систему дифференциальных уравнений
Решение. Составим и решим характеристическое уравнение
Для простого корня
находим Для кратного корня
Ее порядок n=3, а ранг r=2. число линейно независимых собственных векторов равно
Чтобы найти коэффициенты a,b,...., подставляем (6) в исходную систему и приравниваем коэффициенты при подобных членах. Получаем систему
Общее решение этой системы есть Подставив найденные значения a,b,... в (6), и прибавив частное решение, умноженное на
В случае, когда имеются комплексные корни Пример 3. Решить систему дифференциальных уравнений Решение. Составим и решим характеристическое уравнение
Для корня
Можно взять Так как данная система с вещественными коэффициентами, то решение, соответствующее корню
Общее решение выражается через два найденных линейно независимых решений:
Общее решение системы (2) также можно найти, пользуясь методом Эйлера, который заключается в следующем. Ищем решение уравнения (2') в виде
где
Это характеристическое уравнение. Пусть
Векторы
Произвольная линейная комбинация векторов (*)
где Если же, среди корней характеристического уравнения имеется корень
где В этом случае произвольная линейная комбинация векторов (*) и (**) составляет общее решение уравнения (2'). Пример 4. Решить систему дифференциальных уравнений Решение. Согласно методу Эйлера частные решения системы ищем в виде Подставив предыдущие соотношения в систему, имеем алгебраическую систему
из которой в силу не тривиальности искомых решений следует, что определитель
или
Постоянные
Тогда общее решение исходной системы есть Чтобы решить систему
не приведенную к нормальному виду, надо составить характеристическое уравнение
и найти его корни. После этого решение отыскивается уже изложенным способом. Пример 5. Решить систему дифференциальных уравнений
Решение. Составим и решим характеристическое уравнение
Для корня
Можно взять
Частное решение линейной неоднородной системы с постоянными коэффициентами
можно искать методом неопределенных коэффициентов в том случае, когда функции
где Пример 6. Решить систему дифференциальных уравнений
Решение. Для однородной системы находим корни характеристического уравнения
Тогда общее решение запишется в виде
В исходной системе для функций
Для системы (8)
Для системы (9)
Отыскав значения коэффициентов a,b,..., общее решение исходной системы запишется в виде
Решение неоднородной системы (7) можно найти методом вариации постоянных, если известно общее решение однородной системы с теми же коэффициентами. Для этого в формуле общего решения надо заменить произвольные постоянные Пример 7. Решить систему дифференциальных уравнений
Решение. Легко найти (хотя бы методом исключения) общее решение соответствующей однородной системы
Для определения общего решения неоднородной системы, согласно методу вариации произвольных постоянных, считаем
Отсюда находим
где Другой метод решения системы уравнений (2') основан на непосредственном отыскании фундаментальной матрицы этой системы. Экспонентой
где E - единичная матрица. Свойства матричной экспоненты: a) если AB=BA, то b) если c) матрица Из свойства c) следует, что решение x(t) системы (2'), удовлетворяющее условию Для вычисления матрицы
то, представив J в виде
находим, что Пример 8. Вычислить 1) Решение. 1) По определению матричной экспоненты имеем
Вычислим матрицы
Отсюда видно, что Поэтому
2) Собственные числа данной матрицы
чтобы
Для определения матрицы T получаем уравнение
или
Отсюда
Нетрудно убедится, что обратная матрица к матрице T имеет вид
Таким образом, справедливо равенство
Учитывая равенство
Пример 9. Решить систему дифференциальных уравнений
вычислив матрицу Решение. Собственными числами матрицы A являются
чтобы
Отсюда
Учитывая равенство
Таким образом, любое решение x(t) данной системы уравнений, проходящее при t=0 через точку
Нелинейные системы Система дифференциальных уравнений вида
где Существует два основных метода интегрирования систем (1). 1. Метод исключения. Состоит в сведении системы (1) к одному уравнению n -го порядка или к одному уравнению m - го ( Пример 1. Решить систему нелинейных дифференциальных уравнений
Решение. Представим данную систему в виде
получаем
Третье уравнение системы интегрируется независимо от остальных, и его общее решение имеет вид:
Интегрируя последнее уравнение, находим Исключая из полученных соотношений параметр t, получаем два независимых первых интеграла исходной системы
2. Подбор интегрируемых комбинаций. Интегрируемой комбинацией называется дифференциальное уравнение, которое является следствием системы уравнений (1) и интегрируется в квадратурах; например, имеет вид
где Если имеется k первых независимых интегралов
(интегралы называются независимыми, если между функциями
где Иногда нахождение интегрируемых комбинаций облегчается с помощью так называемой симметричной формы записи системы уравнений (1):
где Пример 2. Решить систему дифференциальных уравнений
Решение. Пользуясь свойством пропорции, имеем
Из соотношений (4) получаем
Из второго соотношения (5)
Соотношение (6) дает еще одну интегрируемую комбинацию:
В итоге после интегрирования полученных комбинаций получаем три первых интегралов исходной системы
Очевидно, что эти интегралы линейно независимы.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.35 (0.009 с.) |

 , (1)
, (1) являются непрерывными функциями на (a,b).
являются непрерывными функциями на (a,b).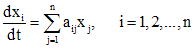 , (2)
, (2)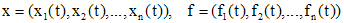 и матрицу
и матрицу 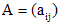 , уравнения (1),(2) можно представить в векторной форме
, уравнения (1),(2) можно представить в векторной форме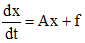 , (1')
, (1') . (2')
. (2') , (3)
, (3)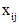 - координаты линейно независимых решений (векторов)
- координаты линейно независимых решений (векторов)
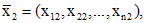

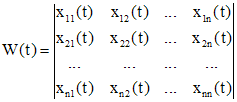 ,
,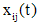 - частные решения системы уравнений (2), была фундаментальной, необходимо и достаточно, чтобы
- частные решения системы уравнений (2), была фундаментальной, необходимо и достаточно, чтобы  при
при 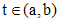 . При этом общее решение векторного уравнения (2') представляется в виде
. При этом общее решение векторного уравнения (2') представляется в виде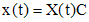 ,
,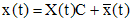 ,
, - какой-нибудь вектор, являющийся частным решением уравнения (1').
- какой-нибудь вектор, являющийся частным решением уравнения (1').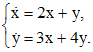
 .
.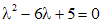 есть
есть 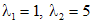 . Следовательно, общее решение последнего уравнения будет
. Следовательно, общее решение последнего уравнения будет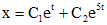 .
.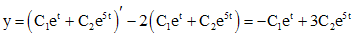 .
. , где x - вектор, A - матрица:
, где x - вектор, A - матрица: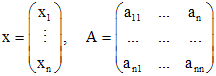 ,
, .
. характеристического уравнения соответствует решение
характеристического уравнения соответствует решение 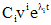 , где
, где  - произвольная постоянная,
- произвольная постоянная, 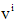 - собственный вектор матрицы A, соответствующий этому
- собственный вектор матрицы A, соответствующий этому  имеется столько линейно независимых собственных векторов
имеется столько линейно независимых собственных векторов 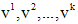 , какова его кратность, то ему соответствует решение
, какова его кратность, то ему соответствует решение 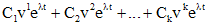 .
.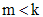 , то решение, соответствующее этому
, то решение, соответствующее этому  , т.е. в виде
, т.е. в виде (4)
(4)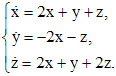
 , (5)
, (5)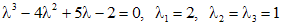 .
.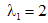 находим собственный вектор
находим собственный вектор 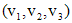 , решая систему
, решая систему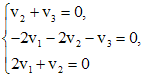
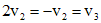 . Значит собственный вектор есть
. Значит собственный вектор есть  , и
, и 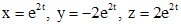 - частное решение исходной системы.
- частное решение исходной системы.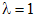 сначала определим число линейно независимых собственных векторов. При
сначала определим число линейно независимых собственных векторов. При  .
. . Корень
. Корень 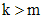 , то решение надо искать в виде произведения многочлена степени
, то решение надо искать в виде произведения многочлена степени  на
на 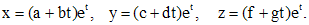 (6)
(6)
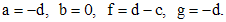 Таким образом, все неизвестные выражены через c и d. Положив
Таким образом, все неизвестные выражены через c и d. Положив  , имеем
, имеем 
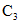 , получим общее решение исходной системы:
, получим общее решение исходной системы: .
. , являются линейно независимыми решениями.
, являются линейно независимыми решениями. .
.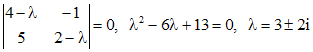 .
.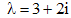 находим собственный вектор
находим собственный вектор  :
: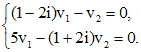
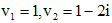 , следовательно, имеет частное решение
, следовательно, имеет частное решение  .
.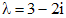 , можно не искать, оно будет комплексно сопряженным с найденным решением. Чтобы получить два вещественных решения, надо взять вещественную и мнимую части найденного комплексного решения. Так как
, можно не искать, оно будет комплексно сопряженным с найденным решением. Чтобы получить два вещественных решения, надо взять вещественную и мнимую части найденного комплексного решения. Так как 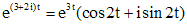 , то
, то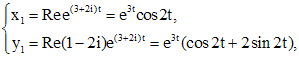

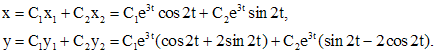
 ,
, - постоянный вектор,
- постоянный вектор,  , где
, где 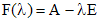 . Поскольку мы ищем нетривиальное решение, то
. Поскольку мы ищем нетривиальное решение, то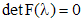 .
. - его простые корни. Тогда соответствующие им решения будут
- его простые корни. Тогда соответствующие им решения будут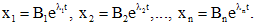 (*)
(*)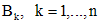 , являются решениями уравнений
, являются решениями уравнений .
. ,
, кратности
кратности 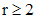 , то соответствующее ему вектор - решение имеет вид
, то соответствующее ему вектор - решение имеет вид , (**)
, (**) - вектор, удовлетворяющий уравнению
- вектор, удовлетворяющий уравнению  .
.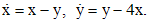
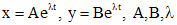 - постоянные.
- постоянные.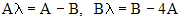 ,
,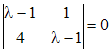 ,
,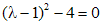 . Корни характеристического уравнения
. Корни характеристического уравнения  - простые. Следовательно, частные решения, им соответствующие, имеют вид:
- простые. Следовательно, частные решения, им соответствующие, имеют вид: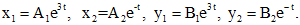
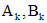 найдем из системы
найдем из системы 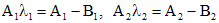 ,
, 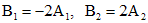 . В силу произвольности
. В силу произвольности  можем, например, положить, что
можем, например, положить, что 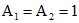 . Тогда
. Тогда  . Таким образом, фундаментальная матрица запишется в виде:
. Таким образом, фундаментальная матрица запишется в виде: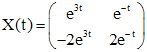 .
.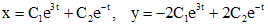 .
.

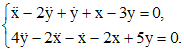
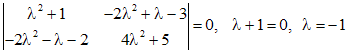 .
. находим собственный вектор
находим собственный вектор 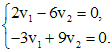
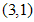 , следовательно, общее решение исходной системы выпишется в виде
, следовательно, общее решение исходной системы выпишется в виде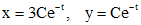 .
.
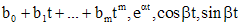 . Это делается по тем же правилам, что и для одного неоднородного уравнения с постоянными коэффициентами, со следующим изменением. Если
. Это делается по тем же правилам, что и для одного неоднородного уравнения с постоянными коэффициентами, со следующим изменением. Если  , где
, где 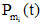 - многочлен степени
- многочлен степени 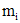 , то частное решение неоднородной системы ищется в не виде
, то частное решение неоднородной системы ищется в не виде  , а в виде
, а в виде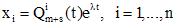 , (7)
, (7) - многочлены степени m+s с неизвестными коэффициентами,
- многочлены степени m+s с неизвестными коэффициентами,  , если
, если 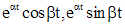 , а число
, а число  является корнем характеристического уравнения.
является корнем характеристического уравнения.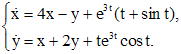
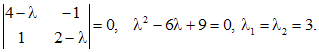
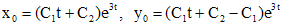 .
.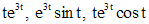 числа
числа 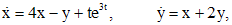 (8)
(8)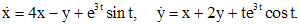 (9)
(9)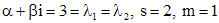 . Согласно (7), частное решение можно искать в виде
. Согласно (7), частное решение можно искать в виде
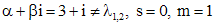 . Частное решение имеет вид
. Частное решение имеет вид

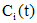 . Полученные выражения для
. Полученные выражения для  надо подставить в данную неоднородную систему, и из этой системы найти
надо подставить в данную неоднородную систему, и из этой системы найти 
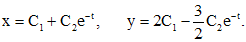
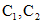 некоторыми дифференцируемыми функциями. Эти функции найдем из системы уравнений, которая получается в результате подстановки значений x и y в неоднородную систему. Таким образом, мы имеем:
некоторыми дифференцируемыми функциями. Эти функции найдем из системы уравнений, которая получается в результате подстановки значений x и y в неоднородную систему. Таким образом, мы имеем: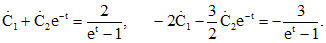
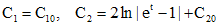 , где
, где  - произвольные постоянные. Подставляя найденные
- произвольные постоянные. Подставляя найденные 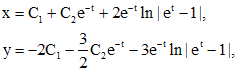
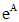 матрицы A называется сумма ряда
матрицы A называется сумма ряда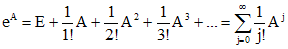 , (10)
, (10)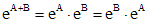 ;
;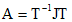 , то
, то 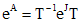 ;
; является решением матричной задачи Коши:
является решением матричной задачи Коши:  , т.е. является фундаментальной матрицей системы (2').
, т.е. является фундаментальной матрицей системы (2').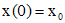 , определяется выражением
, определяется выражением  . Следовательно, задача нахождения решений системы уравнений (2') эквивалентна задаче отыскания матрицы
. Следовательно, задача нахождения решений системы уравнений (2') эквивалентна задаче отыскания матрицы  по матрице A.
по матрице A.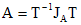 , где
, где  - жорданова форма матрицы A, так как
- жорданова форма матрицы A, так как  . Так как J - клетка Жордана:
. Так как J - клетка Жордана: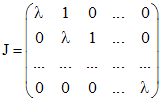 ,
,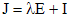 , где
, где ,
,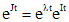 . Матрицу
. Матрицу  легко найти с помощью ряда (10), поскольку
легко найти с помощью ряда (10), поскольку  , где r - размер клетки J, а значит, в нем отличны от нуля только первые r членов.
, где r - размер клетки J, а значит, в нем отличны от нуля только первые r членов. 2)
2) 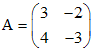 .
.
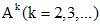 :
: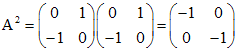 ;
; ;
; .
.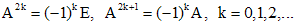
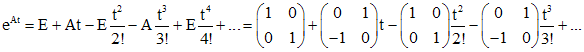
 .
. . Найдем такую невырожденную матрицу
. Найдем такую невырожденную матрицу ,
,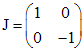 .
.
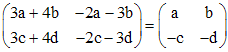 .
. . Одно из решений полученных уравнений есть
. Одно из решений полученных уравнений есть  , поэтому в качестве Tможно взять матрицу
, поэтому в качестве Tможно взять матрицу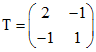 .
.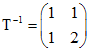 .
.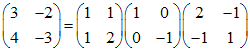 .
. .
.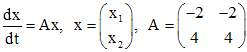 ,
,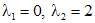 . Найдем такую матрицу
. Найдем такую матрицу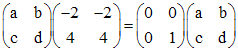 .
. . Одно из решений полученных уравнений есть
. Одно из решений полученных уравнений есть 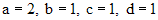 . Поэтому
. Поэтому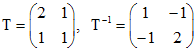 .
.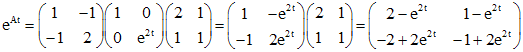 .
. , запишем в виде
, запишем в виде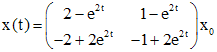 .
. (1)
(1) - неизвестные функции, называется нормальной системой дифференциальных уравнений.
- неизвестные функции, называется нормальной системой дифференциальных уравнений. ) порядка и к системе m независимых уравнений. Такое сведение достигается путем дифференцирования одного из уравнений системы (1) и последующего использования всех уравнений этой же системы.
) порядка и к системе m независимых уравнений. Такое сведение достигается путем дифференцирования одного из уравнений системы (1) и последующего использования всех уравнений этой же системы. .
. ,
, .
. . К первым двум применяется метод исключения, в результате чего имеем:
. К первым двум применяется метод исключения, в результате чего имеем: . (2)
. (2)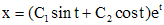 . Подставив x в первое соотношение (2), получим
. Подставив x в первое соотношение (2), получим  .
. .
. ,
, есть решения системы (10). Функция
есть решения системы (10). Функция  , которая тождественно равна постоянной при подстановке в нее решений
, которая тождественно равна постоянной при подстановке в нее решений  (3)
(3) не существует связи вида
не существует связи вида  ), то из системы (13) можно выразить k неизвестных функций через остальные. Подставив их в систему (11), придем к задаче об интегрировании системы уравнений с меньшим числом неизвестных. В частности, если k=n, то все неизвестные функции определяются из системы интегралов (3). Аналитическая форма проверки независимости интегралов имеет вид
), то из системы (13) можно выразить k неизвестных функций через остальные. Подставив их в систему (11), придем к задаче об интегрировании системы уравнений с меньшим числом неизвестных. В частности, если k=n, то все неизвестные функции определяются из системы интегралов (3). Аналитическая форма проверки независимости интегралов имеет вид ,
,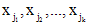 - какие-нибудь k - функций из числа неизвестных.
- какие-нибудь k - функций из числа неизвестных. ,
, .
. .
. , (4)
, (4) , (5)
, (5) . (6)
. (6) .
.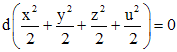 .
. .
. .
.


