
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подпространства линейных пространствСодержание книги
Поиск на нашем сайте
Определение 22. Подпространством линейного пространства называется такое множество его элементов, которое само является линейным пространством над тем же полем. Теорема 14. Непустое множество элементов В Ì L является линейным подпространством в L тогда и только тогда, когда для любых двух элементов в1 и в2 из В и любого lÎ Р выполняются условия: в1 + в2 Î В и l× в1 Î В. Доказательство. Þ Если В – линейное подпространство, то условия теоремы, очевидно, выполнены. Ü Если условия теоремы выполняются, то возьмём любой элемент в Î В. Тогда (–1)× в = – в принадлежит В. Итак, в В для каждого элемента есть противоположный. Но тогда и в + (– в) тоже принадлежит В, т.е. 0 Î В. Остальные требования определения 14 выполняются очевидно. Следовательно, В – линейное пространство над тем же полем, что и L. Примеры линейных подпространств. 1. Пусть а1, а2, …, ак – любая система векторов из L. Множество всех линейных комбинаций этих векторов (т.е. элементов вида a1 а1 + a2 а2 + … + aк ак) называется линейной оболочкой данной системы векторов и обозначается á а1, а2, …, ак ñ, или L (а1, а2, …, ак). Линейная оболочка любой конечной системы векторов из L является линейным подпространством в L.. Одним из базисов линейной оболочки является максимальная линейно независимая подсистема системы а1, а2, …, ак. Следовательно, размерность линейной оболочки равна рангу этой системы. 2. Множество многочленов степени не выше к (к £ n) с коэффициентами из поля Р является линейным подпространством в пространстве многочленов степени не выше n. 3. Множество компланарных геометрических векторов является линейным подпространством в пространстве всех геометрических векторов трёхмерного евклидова пространства. 4. Нулевой вектор является линейным подпространством в том линейном пространстве, которому он принадлежит. 5. Множество диагональных матриц порядка n является линейным подпространством во множестве квадратных матриц порядка n. Пусть А и В – два линейных подпространства пространства L. Определение 23. Суммой подпространств А и В называется множество всех возможных элементов вида а + в, где а Î А, в Î В. (Обозначение А + В) Теорема 15. Сумма линейных подпространств из L есть линейное подпространство из L.
Доказательство. Пусть а1 + в1 и а2 + в2 – любыедва элемента из А + В. Тогда (а1 + в1) + (а2 + в2) = (а1 + а2) + (в1 + в2) Î А + В, так как а1 + а2 Î А, в1 + в2 Î В. Кроме того l×(а + в) = l× а + l× в Î А + В, так как l× а Î А, l× в Î В. Следовательно, по теореме 14 сумма А + В является линейным подпространством в L. Теорема 16. Пересечение линейных подпространств из L есть линейное подпространство из L. Доказательство проведите самостоятельно. Теорема 17. Размерность суммы двух линейных подпространств равна сумме размерностей слагаемых минус размерность их пересечения. Доказательство. Пусть С = А + В, где А и В линейные подпространства пространства L. Пусть D = А Ç В. Выберем базис d = (d1, d2, …, d к) в подпространстве D и дополним его векторами е = (е1, е2, …, еm)и f = (f1, f2 …, fs) так, чтобы система (е1, е2, …, еm, d1, d2, …, d к) была базисом в подпространстве А, а система (d1, d2, …, d к, f1, f2 …, fs) была базисом в В. Покажем, что система (е1, е2, …, еm, d1, d2, …, d к, f1, f2 …, fs) является базисом в подпространстве С. Если с Î С, то с = а + в. Так как а Î А, то а есть линейная комбинация векторов систем е и d. Так как в Î В, то в есть линейная комбинация векторов систем d и f. Но тогда с линейно выражается через векторы е, d и f. Остаётся показать, что система векторов (е1, е2, …, еm , d1, d2, …, d к, f1, f2 …, fs) линейно независима. Для этого рассмотрим a1 е1 + a2 е2 + … + am еm + b1 d1 + b2 d2 +... + bк dк + g1 f1 + g2 f2 + … + gs fs = 0. Вектор а = a1 е1 + a2 е2 + … + am еm + b1 d1 + b2 d2 +... + bк dк лежит в подпространстве А. Но в то же время а = – g1 f1 – g2 f2 – … – gs fs. Следовательно, а Î В. Итак, а Î D. Если бы а не был нулевым вектором, то он не мог бы выражаться через векторы системы f. Следовательно, – g1 f1 – g2 f2 – … – gs fs = 0. Так как векторы системы f линейно независимы, то g1= g2= …= gs = 0. Но тогда a1 е1 + a2 е2 + … + am еm + b1 d1 + b2 d2 +... + bк dк = 0. Так как система векторов (е, d) линейно независима, то отсюда следует, что a1 = a2 = … = am = b1 = b2 = … = bк = 0. Итак, система (е1, е2, …, еm, d1, d2, …, d к, f1, f2 …, fs) является базисом в подпространстве С. Отсюда dim C = m + k + s = (m + k) + (k + s) – k = dim A + dim B – dim D. Изоморфизм линейных пространств Определение 24. Два линейных пространства L и L1 над одним и тем же полем Р называются изоморфными, если существует такое взаимнооднозначное отображение j: L ® L1, что для любых векторов а и в из L и любого элемента l Î Р выполняются условия: j(а + в) = j(а) + j(в), j(l а) = lj(а).
Отображение j называется изоморфизмом. Определение 24 можно заменить следующим эквивалентным определением. Определение 25. Два линейных пространства L и L1 над одним и тем же полем Р называются изоморфными, если существует такое взаимнооднозначное отображение j: L ® L1, что для любых векторов а и в из L и любых элементов l, m Î Р выполняется условие: j(l а + m в) = lj(а) + mj(в). Свойства изоморфизма. 1. j(0) = 01, где 0 и 01 – нулевые вектора в пространствах L и L1 соответственно. 2. Если а1, а2, …, ак – любая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то j(a1 а1 + a2 а2 + … + aк ак) = a1 а11 + a2 а21 + … + aк ак1. 3. Если а1, а2, …, ак –линейно независимая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то система векторов а11, а21, …, ак1 – линейно независима в L1. 4. Если а1, а2, …, ак –линейно зависимая система векторов из L и j(а1) = а11, j(а2) = а21, …, j(ак) = ак1, то система векторов а11, а21, …, ак1 – линейно зависима в L1. 5. Если L – n- мерное линейное пространство, то L1 – тоже n -мерное линейное пространство. 6. При изоморфизме образом любого базиса из L является базис из L1. Примеры изоморфных пространств. 1. Арифметическое линейное пространство Аn над полем Р изоморфно пространству многочленов степени не выше (n – 1) с коэффициентами из поля Р. 2. Пространство квадратных матриц порядка n с элементами из поля Р изоморфно арифметическому линейному пространству размерности n2 над полем Р.
V. РАНГ МАТРИЦЫ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Ранг матрицы Пусть Р некоторое фиксированное поле и пусть А = Определение 26. Столбцевым рангом матрицы А называется ранг системы её векторов – столбцов. По аналогии со столбцами каждую строку матрицы А можно рассматривать как n -мерный вектор из n- мерного арифметического пространства Аn. Определение 27. Строчным рангом матрицы А называется ранг системы её векторов – строк. Теорема 18. Столбцовый ранг матрицы равен наибольшему порядку среди отличных от нуля её миноров. Доказательство. Если все элементы матрицы – нули поля Р, то все её столбцы – нулевые вектора. Ранг этой системы векторов равен нулю. В матрице А все миноры первого порядка, все миноры второго порядка и т.д. равны нулю. Можно считать, что максимальный порядок отличных от нуля миноров равен нулю. Пусть в матрице А не все элементы равны нулю, тогда в матрице есть отличные от нуля миноры. Выберем минор наибольшего порядка среди всех отличных от нуля. При перестановке столбцов ранг системы векторов-столбцов не изменится. При перестановке строк матрицы изменится только порядок координат векторов (при этом у всех векторов одинаково). Следовательно, эта перестановка тоже не изменит ранга системы векторов-столбцов. Переставим, если нужно, строки и столбцы матрицы так, чтобы выбранный нами минор М располагался в левом верхнем углу матрицы. Пусть его порядок равен к. Рассмотрим систему векторов-столбцов матрицы А. Обозначим их а1, …, ак, ак+1, …, аn. Векторы а1, …, ак линейно независимы, иначе выбранный нами минор был бы равен нулю. Покажем, что любой другой вектор-столбец через них линейно выражается. Для этого окаймим выбранный минор любым
Если номер столбца s зафиксирован, то алгебраические дополнения Ар1, …, Арк не меняются при изменении номера строки р. Следовательно, аs = Следствие. Строчный ранг матрицы равен её столбцовому рангу. Доказательство. Транспонируем матрицу А. При этом векторы-строки матрицы А станут векторами-столбцами транспонированной матрицы АТ. П ри транспонировании матрицы транспонируются и все её миноры. Так как при транспонировании определитель не меняется, то максимальный порядок отличных от нуля миноров в матрицах А и АТ один и тот же. По доказанной теореме столбцовые ранги этих матриц равны. Отсюда и следует утверждение следствия. Так как столбцовый и строчный ранги матриц равны, то можно дать определение: Определение 28. Рангом матрицы называется ранг системы её векторов-столбцов (или векторов-строк). Из теоремы о ранге матрицы следует, что если мы найдём в матрице А минор М к- го порядка, отличный от нуля, то среди миноров (к + 1)-го порядка достаточно рассмотреть только те, которые получаются окаймлением минора М. Если они все равны нулю, то ранг матрицы равен к. В дальнейшем минор наибольшего порядка среди отличных от нуля будем называть базисным минором. Пример. Найти ранг матрицы А = Решение. Так как не все элементы матрицы равны нулю, то её ранг не меньше 1. Так как второй т третий столбцы одинаковы, то один из ни можно отбросить и находить ранг матрицы А1 =
Итак, при b = 0 rang A, при b ¹ 0 rang A = 3. Теорема 19. Элементарные преобразования матрицы не меняют её ранга. Доказательство следует из того, что при элементарных преобразованиях матрицы мы получаем эквивалентные системы её векторов-строк.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.253.168 (0.008 с.) |

 произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m- мерныйвектор из m -мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m- мерныхвекторов а1 = (а11, а21, …, аm1), а2 = (а12, а22, …, аm2), …, аn = (а1n, а2n, …, аmn).
произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m- мерныйвектор из m -мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m- мерныхвекторов а1 = (а11, а21, …, аm1), а2 = (а12, а22, …, аm2), …, аn = (а1n, а2n, …, аmn).
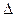 равнее нулю при любом s, равном к + 1, …, n и любом р, равном 1, 2, …, m.
равнее нулю при любом s, равном к + 1, …, n и любом р, равном 1, 2, …, m.
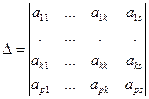 = 0.
= 0.
 Так как М ¹ 0, то
Так как М ¹ 0, то  .
.
 а1 – … –
а1 – … – 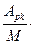 ак. Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров.
ак. Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров. в зависимости от b.
в зависимости от b. . Из миноров второго порядка только один
. Из миноров второго порядка только один 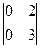 не содержит b, но этот минор равен 0. Рассмотрим минор М1 =
не содержит b, но этот минор равен 0. Рассмотрим минор М1 =  При b = 0 матрица А1 имеет вид
При b = 0 матрица А1 имеет вид  . В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если
. В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если  , то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 =
, то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 =  . Так как
. Так как 


