
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Системы линейных уравнений. Метод ГауссаСодержание книги
Поиск на нашем сайте
ЛИНЕЙНАЯ АЛГЕБРА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ГОУ «Пермский государственный национальный исследовательский университет»
З.И.Андреева
ЛИНЕЙНАЯ АЛГЕБРА Учебное пособие
Пермь 2011
ББК УДК А 655 Библиогр. назв. ISBN
Учебное пособие «Линейная алгебра» написано на основе курса лекций по линейной алгебре, читаемого автором в течение многих лет для студентов физического факультета Пермского государственного университета. Пособие может быть использовано студентами всех направлений физического факультета университета, а также студентами соответствующих специальностей педагогических вузов.
ББК УДК ©Андреева З.И., 2011-02-06 ISBN
.
ВВЕДЕНИЕ Настоящее пособие представляет собой изложение курса лекций по линейной алгебре, которые читаются студентам всех направлений физического факультете Пермского государственного университета. При написании пособия учтены многие достоинства наиболее распространенных учебников, содержащих материалы по линейной алгебре: А.Г.Куроша «Курс высшей алгебры», А.И.Кострикина «Основы алгебры», В.А.Ильина и Э.Г.Позняка «Линейная алгебра», Г.С.Шевцова «Линейная алгебра: теория и прикладные задачи». Приводятся в основном наиболее краткие доказательства. Ссылки на эти учебники в тексте данного пособия мы не делаем. Изложен только программный материал курса. Приведены все необходимые определения, понятия, утверждения и теоремы. Некоторые утверждения (например, теоремы Крамера, Лапласа, о равенстве числа векторов во всех базисах данного конечномерного линейного пространства и др.) приводятся в пособии без доказательства. Для самостоятельного доказательства предлагаются достаточно простые утверждения или утверждения, аналогичные уже доказанным. В пособии приведены образцы решения задач, использующие изложенную теорию.
Перестановки и подстановки Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т.е.
= Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки. Пусть дан упорядоченный набор из n элементов. Элементы этого набора занумеруем числами 1, 2, 3, …, n. Очевидно, вместо того, чтобы говорить об элементах, можно говорить об их номерах. Определение 4. Перестановкой из n чисел (или n символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений). Теорема 1. Число перестановок из n символов равно n! Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами. Говорят, что числа к и р образуют в перестановке (… к…р…) инверсию, если к > р, но в перестановке к стоит раньше р. Перестановка называется чётной, если она содержит чётное число инверсий. Перестановка называется нечётной, если она содержит нечётное число инверсий. Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий. 2) Перестановка (2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий.
Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется транспозицией. Теорема 2. Всякая транспозиция меняет чётность перестановки. Доказательство. Пусть в перестановке символы к и р меняются местами. При этом возможны два случая. 1) Символы к и р в данной перестановке стоят рядом, т.е. (… к, р …). После транспозиции получится перестановка (…. р, к …). Если к и р составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые к и р составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т.е. чётность перестановки изменится. 2) Символы к и р в данной перестановке стоят не рядом, т.е. (…. к,…,р…). После транспозиции получится перестановка (… р,…,к…). Число инверсий, которые к и р составляли в данной перестановке с символами, стоящими перед к и после р, не изменится. Если между к и р стоят m символов, то переставить к и р можно следующим образом: переставить к последовательно с каждым из этих m символов, затем переставить к и р, затем в обратном порядке переставить р с каждым из этих m символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась. Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!. Определение 5. Подстановкой из n символов (или подстановкой n-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя. Элементы данного множества будем обозначать 1, 2, …, n. Подстановка А может быть записана так: если число к переходит в число a к, то А = А = Запись подстановки А = Подстановка Е = Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А = Аналогично получаем, что В×А =
Определители n-го порядка Пусть А = Определение 6. Определителем матрицы А (определителем n-го порядка) называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «-» в противном случае. Обозначение определителя: | А | = Например, при n = 6 произведение а21а13а62а34а46а55 является членом определителя, так как в него входит точно по одному элементу из каждой строки и из каждого столбца. Подстановка, составленная из его индексов будет Произведение а21а13а62а34а46а15 не является членом определителя, так как в него входят два элемента из первой строки. Свойства определителей. 10. При транспонировании определитель не меняется (напомним, что транспонирование матрицы и определителя означает перемену строк и столбцов местами). Действительно, если (-1)к 20. Если все элементы строки (или столбца) определителя равны нулю, то определитель равен нулю. Это следует из того, что по одному элементу указанной строки (или столбца) будет входить в каждый член определителя.
30. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя. Действительно, если все элементы к-ой строки имеют общий множитель l, то их можно записать в виде 40. Если две строки определителя поменять местами, то определитель сменит знак. Действительно, если (-1)к 50. Если две строки определителя пропорциональны, то определитель равен нулю. Действительно, пусть все элементы к-ой строки равны соответствующим элементам р-ой строки, умноженным на l, т.е. | А | = 60. Если в определителе все элементы к-ой строки есть суммы двух слагаемых, то определитель равен сумме двух определителей, в которых все строки, кроме к-ой, такие же как и в данном определителе. На месте элементов к-ой строки одного из них стоят первые слагаемые элементов к-ой строки данного определителя, а на месте элементов к-ой строки второго – вторые их слагаемые. Пусть элементы к-ой строки будут (-1)s Собрав все первые слагаемые, мы получим определитель, отличающийся от данного только к-ой строкой. На месте к-ой строки будут стоять 70. Если к одной строке определителя прибавить другую его строку, все элементы которой умножены на одно и то же число, то определитель не изменится. Это свойство является следствием двух предыдущих. Если в определителе | А | вычеркнуть к-ую строку и р-ый столбец, то останется определитель (n–1)-го порядка. Он называется минором, дополнительным для элемента 80. Дополнительный минор и алгебраическое дополнение не зависит от того, какой элемент стоит в к-ой строке и р-ом столбце определителя. Лемма 1 D = Доказательство. Если а11 = 0, то равенство (8) очевидно. Пусть а11 ¹ 0. Так как в каждый член определителя входит точно один элемент из первой строки, то ненулевыми членами определителя могут быть только те, в которые входит а11. Все они имеют вид
Лемма 2. D = Доказательство. В определителе D переставим р-ую строку последовательно с каждой предыдущей. При этом р-ая строка займёт место первой строки, но минор, дополнительный к элементу арк не изменится. Всего будет сделано (р – 1) перестановка строк. Если новый определитель обозначить D1, то D = (-1)р-1×D. В определителе D1 переставим к -ый столбец последовательно с каждым предыдущим столбцом, при этом будет сделано (к – 1) перестановка столбцов и минор, дополнительный к арк, не изменится. Получится определитель D2 = Теорема 3. Определитель равен сумме произведений элементов некоторой строки на их алгебраические дополнения, т.е. D = ак1Ак1 + ак2×Ак2 +…+аkn×Аkn (10). Доказательство. Пусть D = Теорема 4. Сумма произведений элементов одной строкиопределителя на алгебраические дополнения соответствующих элементов другой строки равна нулю. Доказательство. Пусть D = D = Замечание. Теоремы 3 и 4 будут верны, если в их формулировках слово «строка» заменить на слово «столбец». Способ вычисления определителя n-го порядка. Для вычисления определителя n -го порядка достаточно в какой-нибудь строке (или столбце) получить как можно больше нулей, используя свойство 70, а потом использовать теорему 3. При этом вычисление определителя n-го порядка сведётся к вычислению определителя (n – 1)-го порядка. Пример. Вычислите определитель D = Решение. Получим нули во второй строке. Для этого второй столбец 1) умножим на (-2) и прибавим к первому столбцу; 2) прибавим к третьему столбцу; 3) умножим на (-4) и прибавим к четвёртому столбцу. Получим, что D = D = Некоторые определители (например, такие, в которых стоят «большие» миноры, целиком состоящие из нулей) удобно разлагать по нескольким строкам. Это позволяет делать теорема Лапласа. Пусть в определителе D выделен минор М s-го порядка, элементы которого стоят на строках с номерами к1,к2,…,кs и на столбцах с номерами р1,р2,…,рs. Вычеркнем строки и столбцы с указанными номерами. После этого останется определитель (n – s)-го порядка. Его называют минором М1, дополнительным к минору М. Если s = к1+…+ кs + р1+…+рs, то алгебраическим дополнением к минору М называется А = ( -1)s× М1. Теорема 5 (теорема Лапласа). Пусть в определителе n -го порядка выделены к строк (или столбцов). Определитель равен сумме произведений всех миноров, стоящих на выделенных строках, на их алгебраические дополнения. Доказательство этой теоремы опустим. Пример. Теорема 6 (теорема Крамера). Если в системе линейных уравнений число неизвестных равно числу уравнений и определитель D системы отличен от нуля, то система имеет решение и только одно. Это решение получается по формулам Доказательство. Пусть дана система Используя теоремы 3 и 4, получим х1 ×0 + … + хк ×D + … + хn ×0 = D к, где D к =
III. МАТРИЦЫ
Простые и двойные суммы Введём некоторые общематематические понятия и обозначения. Определение 9. Сумма вида а1 + а2 + … +аn называется простой суммой и обозначается Свойства простых сумм: 10. Определение 10. Сумма вида Свойства двойных сумм: 10.
Умножение матриц Пусть А – матрица размерности m´n и В – матрица размерности n´ к. Произведением матрицы А на матрицу В называется матрица С, элементы которой получаются следующим образом: каждый элемент р -ой строки матрицы А умножается на соответствующий элемент q- го столбца матрицы В, полученные произведения складываются и результат ставится в пересечение р- ой строки и q- го столбца матрицы С, т.е. срq = Размерность матрицы С равна m´ к. Пример 1. = Пример 2. Произведение матриц Но даже если А×В и В×А определены, то они не обязаны быть равны. Пример 3. А×В = А×В = В этом примере А×В и В×А определены, но А×В ¹ В×А. Следовательно, для умножения матриц коммутативный закон не имеет места. Можно проверить: 10. Если (А×В) ×С и А× (В×С) определены, то (А×В) ×С = А× (В×С). 20. Если (А + В)× С определено, то (А + В)× С = А×С + В×С. 30. Если А×В определено, то (l А) ×В = l×(А×В).
3.4. Умножение квадратных матриц одного порядка. Произведение любых двух квадратных матриц одного порядка всегда определено. При умножении двух квадратных матриц n-го порядка получится матрица того же порядка. Теорема 7. Определитель произведения квадратных матриц одного порядка равен произведению определителей сомножителей. Доказательство. Пусть А =
умноженный на
Если | А | ¹ 0, то матрица А называется невырожденной, если же | А | = 0, то матрица А вырожденная. Из теоремы 7 следует, что произведение двух невырожденных квадратных матриц одного порядка есть невырожденная матрица того же порядка, если же одна из матриц вырожденная, то их произведение – тоже вырожденная матрица. Квадратная матрица Е = Определение 11. Матрица В называется правойобратной для матрицы А, если В×А= Е и левой обратной для А, если А×В = Е. Возникает вопрос, всякая ли квадратная матрица имеет левую или правую обратную матрицу. Если В – левая или правая обратная матрица, то (по теореме 7) | В |×| А | = | А |×| В | = 1, т.е. матрица А не может быть вырожденной. Пусть А квадратная невырожденная матрица, найдём алгебраические дополнения для всех её элементов. Составим новую матрицу А* следующим образом: алгебраические дополнения элементов к -ой строки матрицы А поставим в к -ый столбец матрицы А*, т.е. А* = А×А*= А*×А = Так как | А | ¹ 0, то матрица В = Теорема 8. Для всякой квадратной невырожденной матрицы существует обратная матрица. Обратная матрица перестановочна с данной матрицей и вычисляется по формуле А-1= Пример 4. Найдите обратную матрицу, если А = Решение. Найдём | А | = 10 + 12 + 0 – 0 + 4 + 12 = 36. Составим присоединённую матрицу, для этого вычислим алгебраические дополнения. А11 =
Решение матричных уравнений Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15). Возможны два случая: 1) матрица А квадратная невырожденная; 2) матрица А - либо вырожденная, либо прямоугольная. 1) Если А – квадратная и| А | ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А-1×В и Х = В×А-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены. 2) А – квадратная матрица, но | А | = 0, либо А - прямоугольная матрица. Если матрица А имеет размерность m´n, а матрица В – размерность р´к, то, при m ¹ р уравнение (14) не имеет решения, а при n ¹ к не имеет решения уравнение (15). Если же m = р, то в уравнении (14) матрица Х должна иметь к столбцов, а в уравнении (15) она должна иметь р строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений. Пример 5. Найдите матрицу Х, если А×Х = В, где А = Из примера 5 следует, что матрица А имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, получим Х = Пример 6. Найдите матрицу Х, если Х×А = В, где А =
IV. ЛИНЕЙНЫЕ ПРОСТРАНСТВА Алгебраические операции Пусть дано некоторое множество М. Будем говорить, что на множестве М задана внутренняя алгебраическая операция, если задан закон (правило), по которому каждой упорядоченной паре элементов а и в из М ставится в соответствие вполне определённый элемент с. Если при этом для любой пары элементов а, в из М соответствующий элемент с всегда тоже принадлежит М, то М замкнуто относительноданной операции. Пусть даны два множества М и К. Будем говорить, что на множестве М задана внешняя алгебраическая операция, если задан закон, по которому для каждой пары элементов а Î М, в Î К ставится в соответствие вполне определённый элемент с Î М. Сложение и умножение действительных чисел – примеры внутренних алгебраических операций на множестве действительных чисел. Умножение вектора на действительное число – пример внешней алгебраической операции на множестве векторов трёхмерного евклидова пространства. Пусть на множестве элементов Р определены две внутренние алгебраические операции: сложение и умножение: при сложении каждой упорядоченной паре элементов а и в из Р взаимнооднозначно соответствует элемент с Î Р (с = а + в); при умножении тоже каждой упорядоченн
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.149.71 (0.015 с.) |


 =
= (7)
(7) . Если в записи подстановки А некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т.е. та же подстановка. Например,
. Если в записи подстановки А некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т.е. та же подстановка. Например, .
. называется тождественной или единичной.
называется тождественной или единичной. , В =
, В =  , то А×В =
, то А×В =  . Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично,
. Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично,  ,
,  , следовательно,
, следовательно,  ;
; 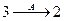 ,
,  , следовательно,
, следовательно,  ;
; 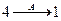 ,
,  , следовательно,
, следовательно,  ;
;  ,
, 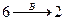 , следовательно,
, следовательно, 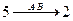 ;
; 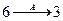 ,
,  , следовательно,
, следовательно,  .
. . Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В) ×С = А× (В×С) для любых подстановок А, В, С одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, если А и Е одного порядка. Для подстановок А =
. Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В) ×С = А× (В×С) для любых подстановок А, В, С одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, если А и Е одного порядка. Для подстановок А =  очевидно А×В = В×А = Е. Следовательно, А-1 = В, т.е. каждая подстановка имеет обратную.
очевидно А×В = В×А = Е. Следовательно, А-1 = В, т.е. каждая подстановка имеет обратную. произвольная квадратная матрица n-го порядка с действительными (или комплексными) элементами.
произвольная квадратная матрица n-го порядка с действительными (или комплексными) элементами. .
. . В ней 4-е инверсии в верхней строке и 2-е инверсии – в нижней. Общее число инверсий равно 6, т.е. подстановка чётная. Следовательно, данное произведение входит в разложение определителя со знаком «+».
. В ней 4-е инверсии в верхней строке и 2-е инверсии – в нижней. Общее число инверсий равно 6, т.е. подстановка чётная. Следовательно, данное произведение входит в разложение определителя со знаком «+».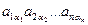 является членом определителя, то все a1, a2, …, an различны и к – число инверсий в перестановке (a1, a2, …, an). При транспонировании номера строк станут номерами столбцов и наоборот. Следовательно, в произведении
является членом определителя, то все a1, a2, …, an различны и к – число инверсий в перестановке (a1, a2, …, an). При транспонировании номера строк станут номерами столбцов и наоборот. Следовательно, в произведении  . Любой член определителя будет иметь вид (-1)s
. Любой член определителя будет иметь вид (-1)s  . Следовательно, из всех членов определителя можно вынести множитель l.
. Следовательно, из всех членов определителя можно вынести множитель l. любой член данного определителя, то в новом определителе номера строк р и q поменяются местами, а номера столбцов останутся прежними. Следовательно, в новом определителе это же самое произведение будет входить в виде (-1)s
любой член данного определителя, то в новом определителе номера строк р и q поменяются местами, а номера столбцов останутся прежними. Следовательно, в новом определителе это же самое произведение будет входить в виде (-1)s  . Так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то к и s имеют противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак.
. Так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то к и s имеют противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак. =
=  = 0.
= 0. + ск1,
+ ск1,  + ск2, ….,
+ ск2, ….,  + скn. Тогда любой член определителя будет иметь вид
+ скn. Тогда любой член определителя будет иметь вид = (-1)s
= (-1)s  + (-1)s
+ (-1)s  .
. и обозначается Мкр. Число (-1)к+р×М кр называется алгебраическим дополнением для элемента
и обозначается Мкр. Число (-1)к+р×М кр называется алгебраическим дополнением для элемента  . (8)
. (8) , где gк и к пробегают значения от 2 до n. Знак этого члена в определителе D определяется чётностью подстановки s =
, где gк и к пробегают значения от 2 до n. Знак этого члена в определителе D определяется чётностью подстановки s =  .Таким образом D есть алгебраическая сумма слагаемых вида
.Таким образом D есть алгебраическая сумма слагаемых вида  , знак которых определяется подстановкой s. Этих слагаемых, очевидно, (n – 1)!. Но подстановка s и подстановка
, знак которых определяется подстановкой s. Этих слагаемых, очевидно, (n – 1)!. Но подстановка s и подстановка  имеют одинаковую чётность. Следовательно, S = М 11. Так как А11 = (-1)1+1× М 11 = М 11, то D = а11×А11.
имеют одинаковую чётность. Следовательно, S = М 11. Так как А11 = (-1)1+1× М 11 = М 11, то D = а11×А11. (9)
(9)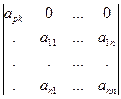 . Очевидно, D2 = (-1)р-1×D1 = (-1)р+к-2×D = (-1)р+к×D. По лемме 1, D2 = арк×М рк. Отсюда D = арк× (-1)р+к × М рк = арк×Арк.
. Очевидно, D2 = (-1)р-1×D1 = (-1)р+к-2×D = (-1)р+к×D. По лемме 1, D2 = арк×М рк. Отсюда D = арк× (-1)р+к × М рк = арк×Арк. . Элементы к-ой строки запишем в виде ак1 =ал1 + 0 + …+ 0, ак2 = 0 + ак2 + 0 + … + 0, …, а
. Элементы к-ой строки запишем в виде ак1 =ал1 + 0 + …+ 0, ак2 = 0 + ак2 + 0 + … + 0, …, а 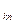 = 0 + 0 + …+ 0 + а
= 0 + 0 + …+ 0 + а  = = ак1Ак1 + ак2Ак2 + … + а
= = ак1Ак1 + ак2Ак2 + … + а  . По предыдущей теореме
. По предыдущей теореме . Если взять
. Если взять  , то в определителе Dбудет две одинаковые строки, т.е. D будет равен нулю. Следовательно, 0 =
, то в определителе Dбудет две одинаковые строки, т.е. D будет равен нулю. Следовательно, 0 =  , если р ¹ к.
, если р ¹ к. .
. . Разложим полученный определитель по элементам второй строки. При этом произведения всех элементов этой строки на их алгебраические дополнения, кроме элемента 1, равны нулю. Для того, чтобы получить алгебраическое дополнение для элемента 1, нужно вычеркнуть те строку и столбец, где этот элемент стоит, т.е. вторую строку и второй столбец. Знак алгебраического дополнения определяет (-1)2+2 = (-1)4 = +1. Итак, D = +
. Разложим полученный определитель по элементам второй строки. При этом произведения всех элементов этой строки на их алгебраические дополнения, кроме элемента 1, равны нулю. Для того, чтобы получить алгебраическое дополнение для элемента 1, нужно вычеркнуть те строку и столбец, где этот элемент стоит, т.е. вторую строку и второй столбец. Знак алгебраического дополнения определяет (-1)2+2 = (-1)4 = +1. Итак, D = +  . Получили определитель 3-го порядка. Этот определитель можно вычислить, используя диагонали и треугольники, но можно свести к определителю второго порядка. Умножим первый столбец 1) на (-4) и прибавим ко второму столбцу, 2) умножим его на 2 и прибавим к третьему столбцу. Получим, что
. Получили определитель 3-го порядка. Этот определитель можно вычислить, используя диагонали и треугольники, но можно свести к определителю второго порядка. Умножим первый столбец 1) на (-4) и прибавим ко второму столбцу, 2) умножим его на 2 и прибавим к третьему столбцу. Получим, что . Следовательно, D = (-1)2+1
. Следовательно, D = (-1)2+1  . Используя свойство 70, прибавим к первому столбцу второй, получим D = -
. Используя свойство 70, прибавим к первому столбцу второй, получим D = -  = -3×(23 – 40) = 51.
= -3×(23 – 40) = 51. = -(1 – 20)(28 + 6) = 19×34 = 661.
= -(1 – 20)(28 + 6) = 19×34 = 661. , где каждое Dк получается из D заменой к-го столбца столбцом свободных членов.
, где каждое Dк получается из D заменой к-го столбца столбцом свободных членов.
 и D ¹ 0. Умножим первое уравнение на А1к, второе – на А2к, …,n- ое уравнение – на Аnк и все уравнения сложим. Получим
и D ¹ 0. Умножим первое уравнение на А1к, второе – на А2к, …,n- ое уравнение – на Аnк и все уравнения сложим. Получим  +…... +
+…... +  + … +
+ … +  =
= 
 (к-ый столбец в определителе D заменён столбцом свободных членов уравнений данной системы). Отсюда
(к-ый столбец в определителе D заменён столбцом свободных членов уравнений данной системы). Отсюда  =
=  для всех к = 1, 2, …, n.
для всех к = 1, 2, …, n. . Следовательно,
. Следовательно,  , 20.
, 20. 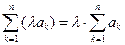 .
. называется двойной суммой и обозначается
называется двойной суммой и обозначается  .
. ; 20.
; 20. 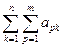 .
. (11).
(11).
 .
. не определено.
не определено. ,
, .
. , В =
, В =  . Составим
. Составим
 , 2-ой столбец, умноженный на
, 2-ой столбец, умноженный на  , …, n- ый столбец,
, …, n- ый столбец,
 . Тогда в (n +1)-м столбце напервых n местах будут стоять элементы первого столбца матрицы А×В, а на остальных местах – нули.
. Тогда в (n +1)-м столбце напервых n местах будут стоять элементы первого столбца матрицы А×В, а на остальных местах – нули.
 называется единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, | Е | = 1.
называется единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, | Е | = 1. . Матрица А* называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что
. Матрица А* называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что = | А |× Е.
= | А |× Е.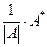 существует и А×В = В×А = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А-1. Итак, получили
существует и А×В = В×А = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А-1. Итак, получили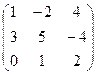 .
. = 14, А12 =
= 14, А12 =  = - 6, А13 =
= - 6, А13 =  = 3, А21 =
= 3, А21 =  = 8, А22 =
= 8, А22 =  = 2, А23 =
= 2, А23 =  = -1, А31 =
= -1, А31 =  = 28, А32 =
= 28, А32 =  = 16, А33 =
= 16, А33 =  = 11. Используя теорему 8, получим А-1 =
= 11. Используя теорему 8, получим А-1 =  .
. .
.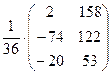 .
. , В =
, В =  . Так как | А | = 0, то для А обратной матрицы нет.По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х =
. Так как | А | = 0, то для А обратной матрицы нет.По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х =  . Тогда Х×А =
. Тогда Х×А =  . Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений.
. Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. 

 Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.
Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.


