
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение матриц. Умножение матрицы на действительное (комплексное) числоСодержание книги
Поиск на нашем сайте Рассмотрим множество M mn всех матриц размерности m´n с действительными (комплексными) элементами. Определение 7. Суммой двух матриц одинаковой размерности называется матрица, каждый элемент которой равен сумме соответствующих элементов данных матриц. Если арк и врк – соответствующие элементы матриц А и В соответственно и С = А + В, то срк = арк + врк. Очевидно, сложение матриц обладает следующими свойствами: · Сумма любых двух матриц одинаковой размерности определена и однозначна. · А + В = В + А для любых матриц А и В из M mn. · (А + В) + С = А + (В + С) для любых А, В, С из M mn. · Матрица, все элементы которой равны нулю, играет роль нуля при сложении и называется нулевой матрицей. Её обозначают О (А + О = А). · Если обозначить - А матрицу, все элементы которой противоположны соответствующим элементам матрицы А, то А + (- А) = О, т.е. матрица (- А) противоположна матрице А. Итак, каждая матрица имеет противоположную. Определение 8. Произведением матрицы А на действительное (или комплексное) число l называется матрица В, все элементы которой равны соответствующим элементам матрицы А, умноженным на l. Если арк – элементматрицы А, то в матрице В элемент врк =l×арк. Умножение матрицы на число обладает следующими свойствами: · Произведение любой матрицы на любое число определено и однозначно. · 1× А = А для любой матрицы А из M mn. · 0× А = О для любой матрицы А из M mn. · (l×g)× А = l×(g× А) для любой матрицы А из M mn и любых чисел l и g. · (l + g)× А = l× А + g× А для любой матрицы А из M mn и любых чисел l и g. · l×(А + В) = l× А + l× В для любых матриц А и В из M mn и любого числа l. · Если А - квадратная матрица n-го порядка, то |l А | = ln×| А |.
Простые и двойные суммы Введём некоторые общематематические понятия и обозначения. Определение 9. Сумма вида а1 + а2 + … +аn называется простой суммой и обозначается Свойства простых сумм: 10. Определение 10. Сумма вида Свойства двойных сумм: 10.
Умножение матриц Пусть А – матрица размерности m´n и В – матрица размерности n´ к. Произведением матрицы А на матрицу В называется матрица С, элементы которой получаются следующим образом: каждый элемент р -ой строки матрицы А умножается на соответствующий элемент q- го столбца матрицы В, полученные произведения складываются и результат ставится в пересечение р- ой строки и q- го столбца матрицы С, т.е. срq = Размерность матрицы С равна m´ к. Пример 1. = Пример 2. Произведение матриц Но даже если А×В и В×А определены, то они не обязаны быть равны. Пример 3. А×В = А×В = В этом примере А×В и В×А определены, но А×В ¹ В×А. Следовательно, для умножения матриц коммутативный закон не имеет места. Можно проверить: 10. Если (А×В) ×С и А× (В×С) определены, то (А×В) ×С = А× (В×С). 20. Если (А + В)× С определено, то (А + В)× С = А×С + В×С. 30. Если А×В определено, то (l А) ×В = l×(А×В).
3.4. Умножение квадратных матриц одного порядка. Произведение любых двух квадратных матриц одного порядка всегда определено. При умножении двух квадратных матриц n-го порядка получится матрица того же порядка. Теорема 7. Определитель произведения квадратных матриц одного порядка равен произведению определителей сомножителей. Доказательство. Пусть А =
умноженный на
Если | А | ¹ 0, то матрица А называется невырожденной, если же | А | = 0, то матрица А вырожденная. Из теоремы 7 следует, что произведение двух невырожденных квадратных матриц одного порядка есть невырожденная матрица того же порядка, если же одна из матриц вырожденная, то их произведение – тоже вырожденная матрица. Квадратная матрица Е = Определение 11. Матрица В называется правойобратной для матрицы А, если В×А= Е и левой обратной для А, если А×В = Е. Возникает вопрос, всякая ли квадратная матрица имеет левую или правую обратную матрицу. Если В – левая или правая обратная матрица, то (по теореме 7) | В |×| А | = | А |×| В | = 1, т.е. матрица А не может быть вырожденной. Пусть А квадратная невырожденная матрица, найдём алгебраические дополнения для всех её элементов. Составим новую матрицу А* следующим образом: алгебраические дополнения элементов к -ой строки матрицы А поставим в к -ый столбец матрицы А*, т.е. А* = А×А*= А*×А = Так как | А | ¹ 0, то матрица В = Теорема 8. Для всякой квадратной невырожденной матрицы существует обратная матрица. Обратная матрица перестановочна с данной матрицей и вычисляется по формуле А-1= Пример 4. Найдите обратную матрицу, если А = Решение. Найдём | А | = 10 + 12 + 0 – 0 + 4 + 12 = 36. Составим присоединённую матрицу, для этого вычислим алгебраические дополнения. А11 =
Решение матричных уравнений Рассмотрим простейшие матричные уравнения вида А×Х = В (14) и Х×А = В (15). Возможны два случая: 1) матрица А квадратная невырожденная; 2) матрица А - либо вырожденная, либо прямоугольная. 1) Если А – квадратная и| А | ¹ 0, то уравнения (14) и (15) имеют единственное решение каждое: Х = А-1×В и Х = В×А-1 соответственно, если эти произведения определены. И не имеют решения, если они не определены. 2) А – квадратная матрица, но | А | = 0, либо А - прямоугольная матрица. Если матрица А имеет размерность m´n, а матрица В – размерность р´к, то, при m ¹ р уравнение (14) не имеет решения, а при n ¹ к не имеет решения уравнение (15). Если же m = р, то в уравнении (14) матрица Х должна иметь к столбцов, а в уравнении (15) она должна иметь р строк. Решение этих матричных уравнений сводится к решению систем линейных уравнений. Пример 5. Найдите матрицу Х, если А×Х = В, где А = Из примера 5 следует, что матрица А имеет обратную, поэтому Х = А-1×В. Используя найденную в примере 5 матрицу А-1, получим Х = Пример 6. Найдите матрицу Х, если Х×А = В, где А =
IV. ЛИНЕЙНЫЕ ПРОСТРАНСТВА Алгебраические операции Пусть дано некоторое множество М. Будем говорить, что на множестве М задана внутренняя алгебраическая операция, если задан закон (правило), по которому каждой упорядоченной паре элементов а и в из М ставится в соответствие вполне определённый элемент с. Если при этом для любой пары элементов а, в из М соответствующий элемент с всегда тоже принадлежит М, то М замкнуто относительноданной операции. Пусть даны два множества М и К. Будем говорить, что на множестве М задана внешняя алгебраическая операция, если задан закон, по которому для каждой пары элементов а Î М, в Î К ставится в соответствие вполне определённый элемент с Î М. Сложение и умножение действительных чисел – примеры внутренних алгебраических операций на множестве действительных чисел. Умножение вектора на действительное число – пример внешней алгебраической операции на множестве векторов трёхмерного евклидова пространства. Пусть на множестве элементов Р определены две внутренние алгебраические операции: сложение и умножение: при сложении каждой упорядоченной паре элементов а и в из Р взаимнооднозначно соответствует элемент с Î Р (с = а + в); при умножении тоже каждой упорядоченной паре элементов а и в из Р взаимнооднозначно соответствует элемент с Î Р (с = а×в). Определение 12. Множество элементов Р называется полем, если на нём заданы две алгебраические операции: сложение и умножение, удовлетворяющие следующим требованиям (аксиомам): 1. Р замкнуто относительно обеих операций; 2. а + в = в + а для любых элементов а и в из Р (коммутативный закон для сложения); 3. (а + в) + с = а + (в + с) для любых элементов а, в и с из Р (ассоциативный закон); 4. $ 0 Î Р такой, что а + 0 = а для любого а Î Р; 5. для любого а Î Р существует (- а) Î Р такой, что а + (- а) = 0; 6. а×в = в×а для любых элементов а и в из Р (коммутативный закон); 7. (а×в) ×с = а× (в×с) для любых элементов а, в и с из Р (ассоциативный закон); 8. $ е Î Р такой, что е×а = а для любого а Î Р (е называетсяединицей и обозначается 1); 9. для любого а Î Р существует а-1 Î Р такой, что а×а-1 = е (а-1 – обратный элемент для а); 10. (а + в) ×с = а×с + в×с для любых элементов а, в и с из Р. Примерами полей являются множество рациональных чисел (R), множество действительных чисел (Q), множество комплексных чисел (С).
4.2. Определение и примеры линейных пространств Пусть даны множество элементов L и поле Р. Элементы из L будем называть векторами. В качестве поля Р будем использовать поле действительных (иногда – комплексных) чисел. Векторы будем обозначать а, в, …; элементы из Р - a, b, l, … Определение 13. Множество элементов L называется линейным (векторным) пространством над полем Р, если на L определены две алгебраические операции: сложение векторов и умножение их на элементы поля Р, удовлетворяющие следующим условиям: 1. L замкнуто относительно обеих операций; 2. а + в = в + а для любых а и в из L.; 3. (а + в) + с = а + (в + с) для любых элементов а,в и с из L; 4. $ 0 Î L такой, что а + 0 = а для любого а Î L; 5. для любого а Î L существует (- а) Î L такой, что а + (- а) = 0; 6. 1× а = а для любого а Î L; 7. (a×b)× а = a×(b× а) для любого а Î L и любых a, b Î Р; 8. (a + b)× а = a× а + b× а для любого а Î L и любых a, b Î Р; 9. a×(а + в) = a× а + a× в для любых а и в из L и любого a Î Р (дистрибутивный закон). Примеры: I. L = í 0 ý, Р – любое поле. II. Множество всех коллинеарных геометрических векторов. III. Множество всех компланарных геометрических векторов. IV. Множество всех возможных геометрических векторов трёхмерного евклидова пространства. V. Множество всех многочленов степени не выше n с действительными (комплексными) коэффициентами. VI. Множество всех многочленов с действительными (комплексными) коэффициентами. VII. Множество всех действительных непрерывных на отрезке [ ав ] функций.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |

 . Следовательно,
. Следовательно,  , 20.
, 20. 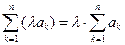 .
. называется двойной суммой и обозначается
называется двойной суммой и обозначается  .
. ; 20.
; 20. 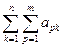 .
. (11).
(11).
 .
. не определено.
не определено. ,
, .
. , В =
, В =  . Составим
. Составим
 , 2-ой столбец, умноженный на
, 2-ой столбец, умноженный на  , …, n- ый столбец,
, …, n- ый столбец,
 . Тогда в (n +1)-м столбце напервых n местах будут стоять элементы первого столбца матрицы А×В, а на остальных местах – нули.
. Тогда в (n +1)-м столбце напервых n местах будут стоять элементы первого столбца матрицы А×В, а на остальных местах – нули.
 называется единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, | Е | = 1.
называется единичной матрицей. Легко проверить, что Е×А = А×Е для любой квадратной матрицы А, имеющей тот же порядок, что и Е. Очевидно, | Е | = 1. . Матрица А* называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что
. Матрица А* называется присоединённой для матрицы А. По правилу умножения матриц и свойствам определителя получаем, что = | А |× Е.
= | А |× Е.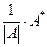 существует и А×В = В×А = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А-1. Итак, получили
существует и А×В = В×А = Е, т.е. матрица В является и левой и правой обратной матрицей для матрицы А. Эта матрица называется обратной матрицей для А и обозначается А-1. Итак, получили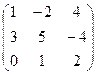 .
. = 14, А12 =
= 14, А12 =  = - 6, А13 =
= - 6, А13 =  = 3, А21 =
= 3, А21 =  = 8, А22 =
= 8, А22 =  = 2, А23 =
= 2, А23 =  = -1, А31 =
= -1, А31 =  = 28, А32 =
= 28, А32 =  = 16, А33 =
= 16, А33 =  = 11. Используя теорему 8, получим А-1 =
= 11. Используя теорему 8, получим А-1 =  .
. .
.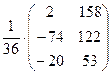 .
. , В =
, В =  . Так как | А | = 0, то для А обратной матрицы нет.По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х =
. Так как | А | = 0, то для А обратной матрицы нет.По правилам умножения матриц, в матрице В столько строк, сколько их в матрице Х, и столько столбцов, сколько их в матрице А. Последнее условие выполняется, следовательно, уравнение имеет решение. На матрицу Х накладывается ограничения: в матрице Х должно быть два столбца и три строки. Чтобы найти элементы такой матрицы, обозначим их и перейдём к системе линейных уравнений. Пусть Х =  . Тогда Х×А =
. Тогда Х×А =  . Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений.
. Полученная матрица равна матрице В тогда и только тогда, когда их соответствующие элементы равны. Получим три системы уравнений. 

 Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.
Эти системы не имеют решений, следовательно, не имеет решения и данное матричное уравнение.


