
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь матриц линейного оператора в разных парах базисовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть даны два линейных пространства Ln и Lm над полем Р. Пусть в Ln зафиксированы базисы е = (е 1, е2, …, еn) и е1 = (е 11, е21, …, еn1), а в пространстве Lm – базисы f = (f1, f2, …, fm) и f1 = (f11, f21, …, fm1). Пусть j: Ln ® Lm линейный оператор, А – его матрица в паре базисов е и f и А1 – матрица этого же оператора в паре базисов е1 и f1. Пусть Т – матрица перехода от базиса е к базису е1, а Q – матрица перехода от f к f1. Тогда е1 = е ×Т, f1 = f ×Q, j (е) = f ×А, j (е1) = f1 ×А1. Отсюда j (е ×Т) = (f ×Q) ×А1, j (е)× Т = f × (Q ×А1). Так как Т – матрица перехода, то она невырожденная, следовательно, существует матрица Т–1. Из последнего равенства получаем, что j (е) = (f × (Q ×А1))× Т–1 = f × (Q ×А1 × Т–1). Но j (е) = f ×А. Следовательно, А = Q ×А1 × Т–1, или А1 = Т ×А×Q–1 (34) Пример. Даны два линейных пространства L3 и L5. Пусть е = (е 1, е2, е3) и f = (f1, f2, f3, f4, f5) – реперы в L3 и L5 соответственно. Пусть а1 = (1, 4, –1, 3, 0), а2 = (3, 0, 1, –3, 7), а3 = (1, 1, 2, 2, 0) – три вектора из L5. Пусть линейный оператор j: L 3 ® L5 задан по правилу j (х1 е1 + х2 е2 + х3 е3) = х1 а1 + х2 а2 + х3 а3. Составить матрицу оператора j и найти образ вектора с = (5, –1, 3). Решение. Для составления матрицы оператора достаточно найти координаты образов базисных элементов пространства L 3 в базисе f пространства L5. По данному правилу получим j (е1) = 1× а1 = (1, 4, –1, 3, 0), j (е2) = 1× а2 = (3, 0, 1, –3, 7), j (е3) = 1× а3 = (1, 1, 2, 2, 0). Составим матрицу, столбцами которой являются координаты найденных векторов.
Итак, j (с) = (5, 23, 0, 24, -7) в пространстве L5. (Сравните с решением этого же примера в пункте 6.1.)
6.5. Линейные преобразования линейного пространства Определение 35. Линейным преобразованием линейного пространства называется линейный оператор данного линейного пространства самого в себя. j: L ® L Всё, что было сказано о линейных операторах, очевидно, верно и для линейных преобразованиях, но некоторые формулы будут иметь более простой вид. Напомним формулы. 1. Если в пространстве Ln зафиксирован базис е = (е 1, е2, …, еn), то матрица А линейного
2. Формулы (35) в матричном виде имеют вид j (е) = е ×А.
3. Связь столбцов координат вектора и его образа: х1 = А × х. 4. Если в пространстве Ln зафиксированы два базиса е = (е 1, е2, …, еn) и е1 = (е 11, е21, …, еn1) и Т – матрица перехода от е к е1, то связь матриц линейного преобразования в этих базисах задаётся формулой А1 = Т ×А×Т–1 (36). Определение 36. Квадратные матрицы А и В называются подобными, если существует такая квадратная невырожденная матрица С, что В = С–1×А×С. 5. Матрицы, задающие линейное преобразование в разных базисах, подобны. 6. Теорема 35. Для любых двух подобных матриц А и В одного и того же порядка n над полем Р и любого линейного пространства Ln над полем Р в Ln существуют такие базисы е и е1, что данные матрицы будут задавать в этих базисах одно и то же линейное преобразование. Доказательство. Пусть В = С–1×А×С. Зафиксируем в Ln какой-нибудь базис. Матрица А в этом базисе задаёт линейное преобразование (пусть это j). Так как матрица С невырожденная, то С–1 может быть матрицей перехода. Пусть е1 = е ×С–1. Тогда преобразование j в базисе е1 будет иметь матрицу С–1×А× (С–1)–1 = С–1×А×С = В. 7. dim (j (Ln)) + dim (Kerj) = n. 8. Множество всех линейных преобразований пространства Ln есть тоже линейное пространство над тем же полем Р, что и пространство Ln. Определение 37. Линейное пространство линейных преобразований линейного пространства Ln называется линейным пространством, сопряжённым пространству Ln. Пространство, сопряжённое Ln, обозначается Ln*. 9. Пространство Ln* изоморфно линейному пространству квадратных матриц порядка n с элементами из поля Р. Следовательно, dim (Ln*) = n 2.
6.6. Невырожденные линейные преобразования Пусть L n – линейное n-мерное пространство над полем Р и пусть j: L n ® Ln – линейное преобразование. Если А –матрица этого преобразования в некотором базисе е, то в любом другом базисе j задаётся матрицей, подобной А, т.е. матрицей вида А1 = Т×А×Т–1. Так как матрица Т невырожденная, то rang (A1) = rang (A). Определение 38. Рангом линейного преобразования линейного пространства называется ранг его матрицы в любом базисе этого пространства. Определение 39. Линейное преобразование линейного пространства называется невырожденным, если его ранг равен размерности пространства. Теорема 36. Линейное преобразование j линейного пространства Ln является невырожденным тогда и только тогда, когда выполняется одно из следующих условий:
1) j (Ln) = Ln; 2) Ker(j) = 0; 3) j – взаимнооднозначное отображение Ln на себя; 4) при преобразовании j различные векторы имеют различные образы.
6.7. Собственные векторы и собственные значения линейного преобразования Пусть L n – линейное n-мерное пространство над полем Р, j: L n ® Ln – линейное преобразование и А –матрица этого преобразования в некотором базисе е. Определение 40. Ненулевой вектор а называется собственным вектором преобразования j, если j (а) = l× а для некоторого l Î Р. Элемент l называется собственным значением преобразования j. По определению собственного вектора, а – собственный вектор преобразования j Û $ l Î Р: j (а) = l× а. Перепишем это равенство в координатах, получим А× х = l× х. Отсюда А× х – (lЕ) × х = О, или (А –lЕ)× х = О. Итак, а – собственный вектор преобразования j Û столбец координат этого вектора является ненулевым решением уравнения (А –lЕ)× х = О (37). Матрица (А –lЕ) называется характеристической матрицей для матрицы А. Матричное уравнение (37) перепишем в виде системы уравнений. Получим, что а – собственный вектор
Корни характеристического многочлена называются характеристическими корнями матрицы А. (Характеристический корень не всегда принадлежит полю Р). Множество всех характеристических корней матрицы А называется её спектром. Согласно определению 40, l Î Р. Пусть l0 Î Р и является характеристическим корнем матрицы А. При l0 система (38) имеет ненулевое решение, т. е. j будет иметь собственный вектор и l0 будет собственным значением преобразования j, заданного матрицей А. Теорема 37. Характеристические многочлены подобных матриц одинаковы. Доказательство. Пусть В = С–1×А×С. Так как матрица lЕ перестановочна с любой матрицей, то | В – lЕ | = | С–1×А×С – lЕ | = | С–1×А×С – С–1 × (lЕ)× С | = | С–1× (А – lЕ)× С | = | С–1 || А – lЕ || С | = | А – lЕ |. Так как матрицы линейного преобразования в разных базисах подобна, то Следствие. Матрицы линейного преобразования в разных базисах имеют один и тот же спектр. Определение 41. Спектр матрицы линейного преобразования в каком-нибудь базисе называется спектром линейного преобразования. Теорема 38. Собственными значениями линейного преобразования j: L n ® Ln, действующего в линейном пространстве над полем Р, являются характеристические корни этого преобразования, принадлежащие полю Р, и только они. Доказательство этой теоремы вытекает из всего сказанного выше. Можно сформулировать следующие правила нахождения собственных значений и собственных векторов линейного преобразования. 1. Записать матрицу данного преобразования в некотором базисе. 2. Составить характеристическое уравнение и найти его корни, принадлежащие полю Р (т.е. найти собственные значения).
3. Если l0 – собственное значение, то составить систему Пример. Найти собственные значения и собственные векторы линейного преобразования j: L4 ® L4 (над полем R), если это преобразование в базисе е = (е 1, е2, е3, е4) имеет матрицу А.
1) (1 – l)2 – 1 = 0, 1 – l = ± 1. Отсюда l1 = 0, l2 = 2. 2) (1– l)×(3 – l) – 6 = 0, l2 – 4 l – 3 = 0, l3 =
Решив последнюю систему, получим х4 =
Решив последнюю систему, получим х3 =
Свойства собственных векторов. 10. Если вектор а – собственный вектор преобразования j, принадлежащий собственному значению l и a ¹ 0, то a× а – тоже собственный вектор, принадлежащий тому же собственному значению. Если j (а) = l а, то j (a а) = aj (а) = a (l а) = l (a а). 20. Множество всех собственных векторов линейного преобразования j: Ln ® Ln, принадлежащих одному и тому же собственному значению (если к ним добавить нулевой вектор), есть линейное подпространство в Ln.
Пусть а и в два собственных вектора и j (а) = l а, j (в) = l в. Тогда j (a а + b в) = aj (а) + bj (в) = a (l а) + b (l в) = l (a а + b в). 30. Собственные векторы, принадлежащие различным собственным значениям, линейно независимы. Пусть j (а) = l а, j (в) = l1 в, l ¹ l1. Если бы а и в были бы линейно зависимы, то хотя бы один из них линейно выражался через другой пусть в = a а. Так как в – собственный вектор, то a ¹ 0. Тогда j (в) = j (a а). Отсюда l1 в = a(l а), l1(a а) = a(l а), a (l1 – l) а = 0. Но в левой части a ¹ 0, l1 – l ¹ 0, а ¹ 0. Противоречие. Следовательно, а и в – линейно независимы. 40. Если в базисе е = (е1, е2,..., ек, …, еn) вектор ек – собственный вектор линейного преобразования j, принадлежащий собственному значению l, то в к -ом столбце матрицы этого преобразования на всех местах, кроме к -го, стоят нули и акк = l.
6.8.Линейные преобразования в базисе из собственных векторов. Линейные преобразования с простым спектром Теорема 39. Линейное преобразование j линейного пространства Ln над полем Р имеет в базисе е = (е1, е2,..., еn) диагональную матрицу тогда и только тогда, когда все векторы базиса являются собственными векторами преобразования j. Доказательство. Þ Пусть матрица А линейного преобразования j в базисе е – диагональная. Тогда j (ек) = lк для любого к = 1, 2, …, n. Но это значит, что все базисные векторы – собственные.. Ü Пусть все базисные векторы –собственные. Тогда j (ек) = lк. Следовательно, в к -ом столбце матрицы этого преобразования на всех местах, кроме к -го, стоят нули и акк = lк. Отсюда и следует, что матрица преобразования – диагональная. Следствие. Квадратная матрица n -го порядка подобна диагональной тогда и только тогда, когда для соответствующего этой матрице линейного преобразования существует базис из собственных векторов. Определение 42. Говорят, что линейное преобразование j линейного пространства Ln над полем Р имеет простой спектр, если все его характеристические корни различны и принадлежат полю Р. Теорема 40. Если линейное преобразование j линейного пространства Ln над полем Р имеет простой спектр, то в Ln существует такой базис, в котором это преобразование имеет диагональную матрицу. Теорема 41. Пусть А – квадратная матрица с элементами из поля Р. Если все характеристические корни матрицы А различны и принадлежат полю Р, то эта матрица подобна диагональной.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К КОЛЛОКВИУМУ
1. Метод Гаусса решения системы линейных уравнений. 2. Определители 2-го и 3-го порядка. 3. Перестановки: определение, свойства. 4. Подстановки: определение, свойства. 5. Определители n -го порядка: определение, свойства, в которых говорится о равенстве определителя нулю. 6. Определители n -го порядка: определение, свойства, в которых говорится, что определитель не изменится. 7. Дополнительные миноры и алгебраические дополнения. Вычисление определителя, в котором все элементы одной строки, кроме одного, равны нулю. 8. Теорема о разложении определителя по элементам строки (столбца). Сумма произведений элементов одной строки на алгебраические дополнения элементов другой строки.
9. Теоремы Лапласа и Крамера. 10. Матрицы. Сложение матриц: определение, свойства. 11. Умножение матрицы на элемент поля Р: определение, свойства. 12. Умножение квадратных матриц. Определитель произведения двух матриц. 13. Обратная матрица. 14. Решение матричных уравнений. 15. Определение и примеры линейных пространств. 16. Арифметическое линейное пространство. 17. Линейно зависимые системы векторов: определение, свойства. 18. Линейно независимые системы векторов: определение, свойства. 19. Базис линейного пространства: определение, примеры, свойства, размерность линейного пространства. 20. Координаты вектора в данном базисе: определение, свойства. 21. Матрица перехода. Связь координат вектора в разных базисах. 22. Подпространства линейных пространств: определение, свойства, примеры. Линейная оболочка системы векторов. 23. Сумма и пересечение линейных подпространств. Теорема о размерности суммы двух конечномерных линейных подпространств. Прямая сумма. 24. Изоморфизм линейных пространств.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.15.215 (0.01 с.) |



 =
= 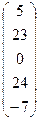 .
.
 ,
столбцы которой – координаты образов
,
столбцы которой – координаты образов
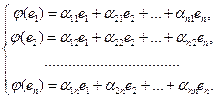 (35)
базисных векторов в базисе е (формулы (35).
(35)
базисных векторов в базисе е (формулы (35).
 (38)
(38)
 (39)
(39)
 и найти её ненулевые решения.
и найти её ненулевые решения. .
.
 (*)
(*)
 , [(1 – l)2 – 1]×[(1– l)×(3 – l) – 6] = 0. Возможны два случая:
, [(1 – l)2 – 1]×[(1– l)×(3 – l) – 6] = 0. Возможны два случая: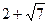 , l4 =
, l4 =  . Итак, характеристическое уравнение имеет четыре корня, все они действительные. Поэтому данное преобразование имеет четыре собственных значения. Для каждого из них составим систему уравнений для нахождения собственных векторов.
. Итак, характеристическое уравнение имеет четыре корня, все они действительные. Поэтому данное преобразование имеет четыре собственных значения. Для каждого из них составим систему уравнений для нахождения собственных векторов.
 Отсюда
Отсюда 
 , х3 =
, х3 =  . Если х1 = 3 С, то х2 = –3 С, х3 = 13 С, х4 = – 11 С, С – любое действительное число, отличное от нуля. Итак, собственными векторами, принадлежащими собственному значению l = 0, являются все ненулевые векторы вида (3 С, – 3 С, 13 С, –11 С).
. Если х1 = 3 С, то х2 = –3 С, х3 = 13 С, х4 = – 11 С, С – любое действительное число, отличное от нуля. Итак, собственными векторами, принадлежащими собственному значению l = 0, являются все ненулевые векторы вида (3 С, – 3 С, 13 С, –11 С).
 Отсюда
Отсюда 
 , х4 =
, х4 =  Если х1 = 7 С, то х2 = 7 С, х3 = –15 С, х4 = –11 С, где С – любое отличное от нуля действительное число. Итак, собственными векторами, принадлежащими собственному значению l = 2, являются все ненулевые векторы вида (7 С, 7 С, –15 С, –11 С).
Если х1 = 7 С, то х2 = 7 С, х3 = –15 С, х4 = –11 С, где С – любое отличное от нуля действительное число. Итак, собственными векторами, принадлежащими собственному значению l = 2, являются все ненулевые векторы вида (7 С, 7 С, –15 С, –11 С).

 , х3 – любое отличное от нуля действительное число. Если х3 = 2 С, то
, х3 – любое отличное от нуля действительное число. Если х3 = 2 С, то  . Итак, собственными векторами, принадлежащими собственному значению l = 2 +
. Итак, собственными векторами, принадлежащими собственному значению l = 2 +  , являются все ненулевые векторы вида (0, 0, 2 С,
, являются все ненулевые векторы вида (0, 0, 2 С, 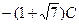 ).
).

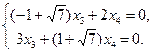
 , х3 – любое отличное от нуля действительное число. Если х3 = 2 С, то
, х3 – любое отличное от нуля действительное число. Если х3 = 2 С, то 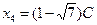 . Итак, собственными векторами, принадлежащими собственному значению l = 2 +
. Итак, собственными векторами, принадлежащими собственному значению l = 2 +  ) С).
) С).




