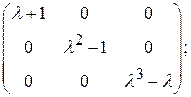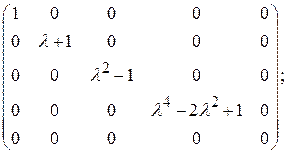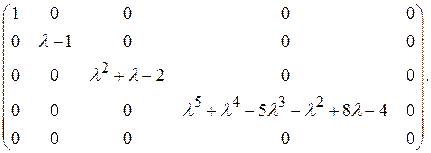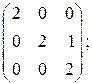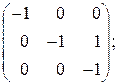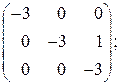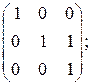Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение матрицы к жордановой нормальной форме.Содержание книги
Поиск на нашем сайте
В предыдущем параграфе мы выяснили, что если матрица ТЕОРЕМА 1. Матрица В самом деле, если матрица Обратно, пусть все характеристические корни матрицы
то
Действительно, определители матрицы Пусть (8) будут разложения многочленов (10) в произведения степеней линейных множителей. Назовем элементарными делителями многочлена
Элементарные делители всех многочленов (10) назовем элементарными делителями матрицы Возьмем теперь жорданову матрицу Пример 5. Найти жорданову нормальную форму матрицы
Решение. Приводя обычным способом матрицу
Мы видим, что матрица
На основании предшествующих результатов может быть доказано, наконец, следующее необходимое и достаточное условие приводимости матрицы к диагональному виду. ТЕОРЕМА 2. Матрица ДОКАЗАТЕЛЬСТВО. В самом деле, приводимость матрицы к диагональному виду равносильна приводимости к такому жорданову виду, все жордановы клетки которого имеют порядок
Минимальный многочлен. Пусть дана квадратная матрица
произвольный многочлен из кольца
будет называться значением многочлена Нетрудно проверить, что если Если многочлен УТВЕРЖДЕНИЕ 1. Всякая матрица ДОКАЗАТЕЛЬСТВО. Известно, что все квадратные матрицы порядка
линейно зависима над полем
Таким образом, матрица
степень которого не превосходит Матрица УТВЕРЖДЕНИЕ 2. Всякий многочлен ДОКАЗАТЕЛЬСТВО. Разделим
тогда
и из того, что Для доказательства основной теоремы данного параграфа потребуется вспомогательное утверждение. ЛЕММА. Пусть
Если
то
ДОКАЗАТЕЛЬСТВО. Достаточно доказать хотя бы первое из двух утверждений леммы
ТЕОРЕМА 1. Минимальный многочлен матрицы ДОКАЗАТЕЛЬСТВО. Как следует из § 3.1
Значит, многочлены
Тогда справедливо равенство
С другой стороны, так как элементами матрицы
причем наибольший общий делитель элементов матрицы Из равенств (5), (6) и (4) вытекает равенство
Это равенство можно сократить на ненулевой множитель
откуда
Это равенство показывает, что остаток от деления Отсюда следует, что многочлен
Ясно, что старший коэффициент многочлена Так как
Равенства (8), (7) и (9) приводят к равенству
Обе части этого равенства можно сократить на общий множитель
Мы помним, однако, что наибольший общий делитель элементов матрицы Так как, ввиду (4), характеристический многочлен матрицы ТЕОРЕМА 2 (Гамильтона
ТЕОРЕМА 3. Если матрицы ДОКАЗАТЕЛЬСТВО. Действительно, пусть Если
Трансформируя обе части этого равенства матрицей
т.е. СЛЕДСТВИЕ. Подобные матрицы обладают одним и тем же минимальным многочленом. □ Пусть теперь Используя операции над линейными операторами [2] можно ввести понятие значения многочлена
из кольца будет линейный оператор
где Будем говорить, что многочлен Учитывая связь между операциями над линейными операторами и над матрицами можно доказать следующее утверждение. ТЕОРЕМА 4. Минимальный многочлен линейного оператора После этого результаты, полученные выше, в частности теорема Гамильтона ЗАДАЧИ К ГЛАВЕ III. 22. Привести следующие а) б) в) г) д) е) ж) з) и) 23. Привести следующие а) б) в) 24. Привести следующие а) б) в) г) д) е) 25. Выяснить, эквивалентны ли между собой следующие а) б)
в)
26. Найти элементарные делители следующих матриц: а) б) в) 27. Найти нормальную диагональную форму квадратной а) б) в) 28. Выяснить, являются ли подобными между собой следующие матрицы: а) б) в) г)
29. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) 30. Выяснить, являются ли следующие матрицы подобными некоторым диагональным матрицам в полях рациональных, вещественных и комплексных чисел: а) б) в) г) 31. Найти минимальные многочлены следующих матриц: а) б) ОТВЕТЫ. 1. а) да; б) нет; в) да; г) да; д) нет. 2. а) да; б) нет; в) да; г) да; д) нет; е) нет; ж) да. 3. а) нет; б) да; в) да; г) нет; д) да; е) нет; ж) да. 4. а) б) в) 5. а) б) 6. а) б) в) 7. а) нет; б) да, в) да, г) нет; д) да, е) да, 8. 9. а) нет; б) да; в) да. 10. Диагональная матрица является ортогональной тогда и только тогда, когда каждый диагональный элемент равен 11. а) б) в) 12. а) нет; б) да; в) нет; г) да. 13. а) б) ни при каком 14. а) б) в) 15. а) б) в) г) д) е) ж) з) и) к) 16. а) б) в) г) д) е) 17. а) б) в) г) д) 18. Ответ определяется неоднозначно. а) б) в) г) д) е) 19. Ответ определяется неоднозначно. а) б) в) г) д) е) ж) з) и) к) л) м) 20. а) положительно определённая; б) не является знакоопределённой; в) не является знакоопределённой; г) положительно определённая; д) отрицательно определённая; е) не является знакоопределённой. 21. а) для любого б) ни при каком значении в) г) д) ни при каком значении е) ж) 22. а) б) в) г) д) е) ж) з) и) 23. а) б) в) 24. а) б) в) г) д) е) 25. а) эквивалентны; б) не эквивалентны; в) матрицы 26. а) б) в) элементарных делителей не существует. 27. а) б) в) 28. а) подобны; б) подобны; в) матрицы г) матрицы
29. а) б) в) г) д) е) ж) з) и) к) л) м) н) о) п) 30. а) в поле рациональных чисел подобна матрице б) в поле вещественных чисел подобна матрице в) в поле комплексных чисел подобна матрице г) не подобна диагональной матрице ни в каком поле. 31. а) б) СПИСОК ЛИТЕРАТУРЫ. 1. Апатенок Р. Ф., Маркина Л. М., Хейнман В. Б. Сборник задач по линейной алгебре и аналитической геометрии. - Минск: Высшая школа, 1990. 2. Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб.: Для ВУЗов. - М.: Физматлит, 2001. 3. Курош А. Г. Курс высшей алгебры. - М.: Наука, 1971. 4. Проскуряков И. В. Сборник задач по линейной алгебре. - М.: Наука, 1984. 5. Шипачёв В. С. Задачник по высшей математике: Учеб. пособие для ВУЗов. - М.: Высшая школа, 2002. СОДЕРЖАНИЕ. ГЛАВА I. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ И УНИТАРНОМ ПРОСТРАНСТВАХ. 3 §1.1. Евклидовы и унитарные пространства. 3 §1.2. Изоморфизм унитарных пространств. 13 §1.3. Линейные функции. 14 §1.4. Сопряжённые операторы. 16 §1.5. Нормальные операторы. 20 §1.6. Унитарные операторы. 22 §1.7. Эрмитовы (самосопряжённые) операторы. 24 §1.8. Кососимметрические операторы. 25 §1.9. Неотрицательные линейные операторы. 26 §1.10. Линейные операторы в евклидовом пространстве. 28 ЗАДАЧИ К ГЛАВЕ I. 34 ГЛАВА II. КВАДРАТИЧНЫЕ ФОРМЫ. 39 §2.1. Приведение квадратичной формы к каноническому виду. 39 §2.2. Приведение квадратичной формы к главным осям. 48 §2.3. Закон инерции. 52 §2.4. Распадающиеся квадратичные формы. 57 §2.5. Положительно определенные формы. 59 §2.6. Пары форм. 65 ЗАДАЧИ К ГЛАВЕ II. 67 ГЛАВА 3. ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА МАТРИЦЫ. 70 §3.1. §3.2. Унимодулярные критерий эквивалентности. 79 §3.3. Матричные многочлены. 83 §3.4. Связь подобия числовых матриц с эквивалентностью их характеристических матриц. 86 § 3.5. Жорданова нормальная форма. 89 § 3.6. Приведение матрицы к жордановой нормальной форме. 97 § 3.7. Минимальный многочлен. 100 ЗАДАЧИ К ГЛАВЕ III. 106 ОТВЕТЫ. 112 СПИСОК ЛИТЕРАТУРЫ. 122 СОДЕРЖАНИЕ. 123
Дмитрий Иванович Иванов
АЛГЕБРА (часть II)
Учебно-методическое пособие
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.202 (0.009 с.) |

 с элементами из поля
с элементами из поля 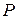 приводится к жордановой нормальной форме, то эта форма определяется для матрицы
приводится к жордановой нормальной форме, то эта форма определяется для матрицы  , то эти две матрицы обладают одними и теми же характеристическими корнями. Характеристические корни матрицы
, то эти две матрицы обладают одними и теми же характеристическими корнями. Характеристические корни матрицы  равен произведению ее элементов, стоящих на главной диагонали, то многочлен
равен произведению ее элементов, стоящих на главной диагонали, то многочлен  разлагается над полем
разлагается над полем 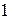 инвариантные множители матрицы
инвариантные множители матрицы  будут
будут , (10)
, (10) .
.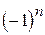 , так как именно таков старший коэффициент характеристического многочлена
, так как именно таков старший коэффициент характеристического многочлена  . Таким образом, среди многочленов (10) нет равных нулю, сумма степеней этих многочленов равна
. Таким образом, среди многочленов (10) нет равных нулю, сумма степеней этих многочленов равна  и все они разлагаются над полем
и все они разлагаются над полем  последнее ввиду того, что, по условию, многочлен
последнее ввиду того, что, по условию, многочлен  обладает таким разложением.
обладает таким разложением. , отличные от единицы степени различных линейных двучленов, входящие в его разложение (8), т. е.
, отличные от единицы степени различных линейных двучленов, входящие в его разложение (8), т. е.
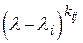 матрицы
матрицы  , относящуюся к числу
, относящуюся к числу  . Очевидно, что отличными от
. Очевидно, что отличными от 

 и
и 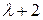 , а поэтому жордановой нормальной формой матрицы
, а поэтому жордановой нормальной формой матрицы  .
.
 ее характеристической матрицы лежат в поле
ее характеристической матрицы лежат в поле  являются делителями многочлена
являются делителями многочлена  , то последнее условие равносильно тому, что все элементарные делители многочлена
, то последнее условие равносильно тому, что все элементарные делители многочлена 
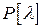 , то матрица
, то матрица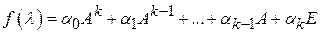
 при
при 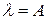 .
. или
или  , то
, то 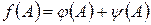 и, соответственно,
и, соответственно,  .
. , то матрицу
, то матрицу  мерное векторное пространство. Отсюда следует, что система из
мерное векторное пространство. Отсюда следует, что система из  матриц
матриц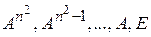
 , не все равные нулю, что
, не все равные нулю, что .
. ,
, . □
. □ этой матрицы.
этой матрицы. ,
,
 следует
следует  , но степень
, но степень  меньше степени
меньше степени  ,
,  . (1)
. (1) (2)
(2) (3)
(3)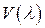 будет заменен его записью (1), вместо
будет заменен его записью (1), вместо  будет подставлено (3), а в качестве
будет подставлено (3), а в качестве  будет взят многочлен
будет взят многочлен
 . (4)
. (4) не будут нулевыми. Обозначим, далее, через
не будут нулевыми. Обозначим, далее, через  матрицу, составленную из алгебраических дополнений матрицы
матрицу, составленную из алгебраических дополнений матрицы 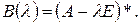
 . (5)
. (5) го порядка матрицы
го порядка матрицы  , (6)
, (6)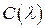 равен
равен  .
. ,
, . (7)
. (7) матрицы
матрицы  слева, на двучлен
слева, на двучлен  равен нулю. Из леммы вытекает, что этот остаток равен матрице
равен нулю. Из леммы вытекает, что этот остаток равен матрице  . Действительно, матрица
. Действительно, матрица  , т. е. многочлен
, т. е. многочлен 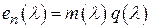 . (8)
. (8) равен единице.
равен единице. , то по лемме остаток от левого деления
, то по лемме остаток от левого деления  на двучлен
на двучлен  . (9)
. (9) .
. этого матричного
этого матричного 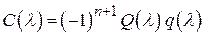 .
. . Таким образом, ввиду (8),
. Таким образом, ввиду (8),  что и требовалось доказать. □
что и требовалось доказать. □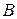 подобны и если многочлен
подобны и если многочлен  .
.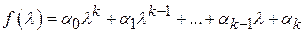 , то
, то .
. , получаем:
, получаем:
 . □
. □ линейный оператор в
линейный оператор в  мерном линейном пространстве над полем
мерном линейном пространстве над полем  .
.
 при
при 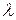 , равном линейному оператору
, равном линейному оператору  ,
,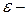 тождественный оператор.
тождественный оператор. аннулируется линейным оператором
аннулируется линейным оператором  , где
, где  нулевой оператор.
нулевой оператор.
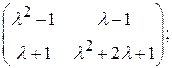


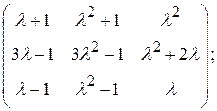


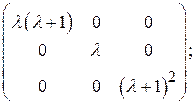

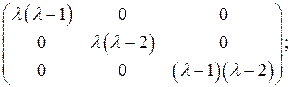
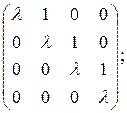


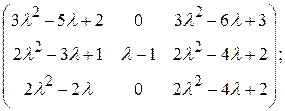





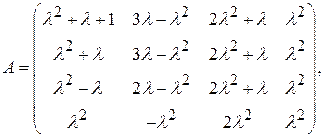







 и порядок
и порядок 

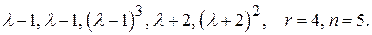



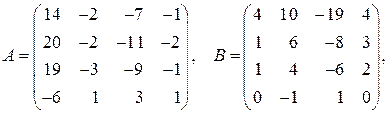





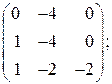

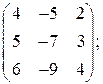




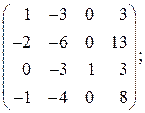
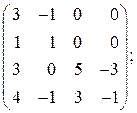








 ;
; ;
; .
. ;
; .
. ;
; ;
; .
.
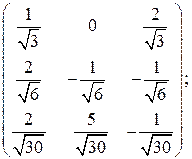


 .
. .
.


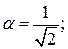







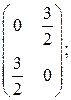
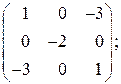
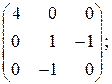




 ;
; ;
; ;
; ;
;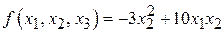 ;
; .
. ;
; ;
; .
.

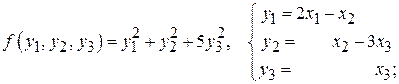



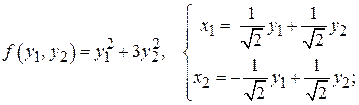
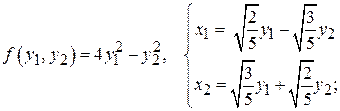







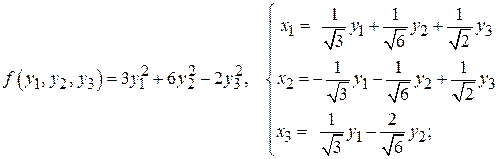

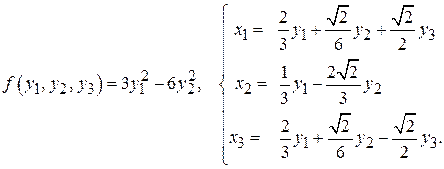
 ;
;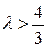 ;
; ;
; ;
;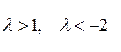 .
.


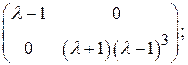


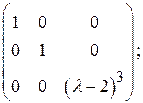







 где
где