Глава I. Линейные операторы в евклидовом и унитарном пространствах.
УДК 512.8
Д. И. Иванов. Алгебра (часть II): Учебно-методическое пособие по дисциплине «Алгебра» для студентов специальности «Компьютерная безопасность». Тюмень: Печатник, 2009, 125 стр.
Данное пособие разработано в соответствии с государственным образовательным стандартом и учебным планом специальности «Компьютерная безопасность» (II семестр), содержит теоретическую часть и комплекс практических заданий.
Рекомендовано к печати Учебно-методической комиссией института математики и компьютерных наук. Одобрено Учебно-методической секцией Учёного совета Тюменского государственного университета.
ОТВЕТСТВЕННЫЙ РЕДАКТОР: В. Н. Кутрунов, д. ф.-м. н., профессор.
РЕЦЕНЗЕНТЫ: А. Н. Дёгтев, д. ф.-м. н., профессор кафедры алгебры и математической логики Тюменского государственного университета.
С. Д. Захаров, к. ф.-м. н., зав. каф. математики информатики и естественных наук Тюменского государственного института мировой экономики управления и права.
© ГОУ ВПО Тюменский государственный университет, 2009
© Д. И. Иванов, 2009
ГЛАВА I. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ И УНИТАРНОМ ПРОСТРАНСТВАХ.
Изоморфизм унитарных пространств.
Два унитарных (или евклидовых) пространства  и и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие  , для которого , для которого
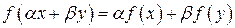 и и  . .
ТЕОРЕМА. (об изоморфизме унитарных пространств). Два унитарных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность.
ДОКАЗАТЕЛЬСТВО. Очевидно, что если  и и  изоморфны, то они являются изоморфными, как линейные пространства. Однако изоморфные линейные пространства имеют одинаковую размерность [1]. изоморфны, то они являются изоморфными, как линейные пространства. Однако изоморфные линейные пространства имеют одинаковую размерность [1].
Обратно, пусть размерности  и и  равны, а равны, а  и и  , соответственно, их ортонормированные базисы. Зададим отображение , соответственно, их ортонормированные базисы. Зададим отображение  следующим образом: если следующим образом: если
 , ,
то считаем
 . .
Это отображение взаимнооднозначно и сохраняет операции сложения и умножения на число. Значит, они изоморфны, как линейные пространства.
Покажем, что  сохраняет скалярное произведение. Рассмотрим два произвольных вектора сохраняет скалярное произведение. Рассмотрим два произвольных вектора
 , ,
 . .
Тогда
 и и

То есть  . □ . □
Линейные функции.
Рассмотрим произвольное линейное пространство  над полем над полем 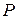 . Отображение . Отображение  называется линейной функцией, если называется линейной функцией, если
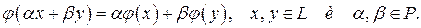
Нетрудно проверить, что если  и и  линейные функции, то линейные функции, то  и и  , такие что , такие что  и и  , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в  образуют линейное пространство относительно их сложения и умножения числа на функцию. образуют линейное пространство относительно их сложения и умножения числа на функцию.
ЛЕММА. (о существовании и единственности линейной функции). Для любого базиса  линейного пространства линейного пространства  и любого набора и любого набора  существует единственная линейная функция существует единственная линейная функция  , такая, что , такая, что
 . .
ДОКАЗАТЕЛЬСТВО. Пусть  произвольный вектор из произвольный вектор из  . Зададим отображение . Зададим отображение  следующим образом: следующим образом:
 , ,
Очевидно, что 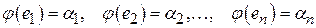 . .
Проверим, что  линейная функция. Пусть линейная функция. Пусть  . Тогда . Тогда
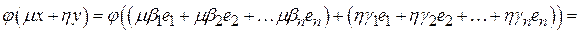


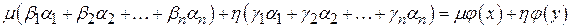 . .
Докажем единственность. Предположим, что существует другая линейная функция  , удовлетворяющая условию леммы, т. е. , удовлетворяющая условию леммы, т. е.
 . Тогда . Тогда  . □ . □
Пусть 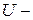 унитарное пространство. Положим по определению унитарное пространство. Положим по определению  для любых для любых 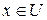 и фиксированного и фиксированного 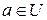 . Тогда имеет место . Тогда имеет место
ТЕОРЕМА. Функция  является линейной и однозначно определяется по является линейной и однозначно определяется по  . Обратно, для каждой линейной функции . Обратно, для каждой линейной функции 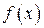 существует элемент существует элемент 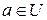 , такой что , такой что  . .
ДОКАЗАТЕЛЬСТВО. Вначале докажем линейность функции. Действительно
 . .
Пусть теперь 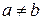 , тогда , тогда  . При . При  имеем имеем  , т. е. , т. е.  . Тем самым показано, что каждому . Тем самым показано, что каждому 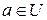 соответствует единственная линейная функция соответствует единственная линейная функция  . .
Наконец, пусть  произвольная линейная функция, заданная в пространстве произвольная линейная функция, заданная в пространстве  . Докажем, что существует элемент . Докажем, что существует элемент 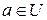 , такой, что , такой, что  для любых для любых 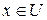 . Пусть . Пусть  ортонормированный базис пространства ортонормированный базис пространства  . По лемме, существует единственный набор . По лемме, существует единственный набор  , такой, что , такой, что  . Рассмотрим вектор . Рассмотрим вектор
 , ,
тогда  . Для произвольного вектора . Для произвольного вектора  , имеем , имеем
 . □ . □
Сопряжённые операторы.
Построим по каждому линейному оператору   мерного унитарного пространства мерного унитарного пространства  оператор оператор  , сопряжённый данному. Выберем в , сопряжённый данному. Выберем в  вектор вектор  и рассмотрим функцию и рассмотрим функцию  переменной переменной  . Эта функция является линейной. Действительно . Эта функция является линейной. Действительно

С другой стороны  , где , где 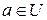 по теореме из предыдущего параграфа определяется однозначно по функции по теореме из предыдущего параграфа определяется однозначно по функции  , т. е. по , т. е. по  и и  . Таким образом, при фиксированном . Таким образом, при фиксированном  для каждого для каждого  имеется единственный вектор имеется единственный вектор  . Оператор . Оператор 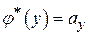 называется сопряжённым к называется сопряжённым к  , т. е. , т. е.

Покажем, что для каждого  сопряжённый оператор сопряжённый оператор  определяется однозначно. Предположим, что существует оператор определяется однозначно. Предположим, что существует оператор  , такой что , такой что  , тогда , тогда 
 . .
Нетрудно убедиться в том, что сопряжённый оператор  является линейным. Действительно является линейным. Действительно

 . .
Значит  . .
Отметим следующие свойства сопряжённого оператора:
1.  ; ;
2.  ; ;
3.  ; ;
4.  . .
Докажем первое свойство.
 . Другие свойства доказываются аналогично. . Другие свойства доказываются аналогично.
Если  квадратная матрица порядка квадратная матрица порядка  , то матрица , то матрица  , полученная из , полученная из  заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если  , то , то 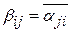 . .
ТЕОРЕМА. Если линейный оператор  в ортонормированном базисе имеет матрицу в ортонормированном базисе имеет матрицу  , то сопряжённый оператор , то сопряжённый оператор  будет иметь в этом базисе сопряжено транспонированную матрицу. будет иметь в этом базисе сопряжено транспонированную матрицу.
ДОКАЗАТЕЛЬСТВО. Пусть в унитарном пространстве  задан ортонормированный базис задан ортонормированный базис  , а матрицы операторов , а матрицы операторов  и и  в этом базисе будут соответственно в этом базисе будут соответственно  , т. е. для любых , т. е. для любых 
 ; ;
 . .
Домножим первое равенство справа на  , получим , получим
 , следовательно , следовательно 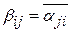 . □ . □
Пример 1. Линейный оператор  задан в евклидовом пространстве в базисе из векторов задан в евклидовом пространстве в базисе из векторов  матрицей матрицей
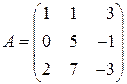 . .
Найти матрицу сопряжённого оператора  в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе. в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе.
Решение. Координаты векторов  заданы в некотором ортонормированном базисе заданы в некотором ортонормированном базисе 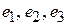 . Матрица перехода от . Матрица перехода от 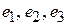 к к  будет будет
 . .
Значит, 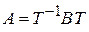 , где , где  матрица того же оператора в ортонормированном базисе. Откуда матрица того же оператора в ортонормированном базисе. Откуда  . .
Находим
 . .
Тогда
 . .
Матрица сопряжённого оператора  будет по предыдущей теореме сопряжено транспонированной, а так как оператор задан в евклидовом пространстве, то просто транспонированной. будет по предыдущей теореме сопряжено транспонированной, а так как оператор задан в евклидовом пространстве, то просто транспонированной.
 . .
Возвращаемся к исходному базису

Нормальные операторы.
Линейный оператор  унитарного пространства унитарного пространства  называется нормальным, если называется нормальным, если
 , ,
т. е. если он перестановочен со своим сопряжённым.
Если  ортонормированный базис пространства ортонормированный базис пространства  и и  матрица нормального оператора матрица нормального оператора  в этом базисе, то по теореме из §1.3 имеем в этом базисе, то по теореме из §1.3 имеем  . .
Справедливы следующие три теоремы о нормальных операторах.
ТЕОРЕМА 1. Всякий собственный вектор  нормального оператора нормального оператора  , соответствующий собственному значению , соответствующий собственному значению 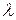 будет и собственным вектором оператора будет и собственным вектором оператора  , который соответствует комплексно-сопряжённому значению , который соответствует комплексно-сопряжённому значению  . .
ДОКАЗАТЕЛЬСТВО. Если  линейный оператор, а линейный оператор, а 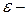 тождественный оператор тождественный оператор  , то , то  также линейный оператор, сопряжённым для которого будет также линейный оператор, сопряжённым для которого будет 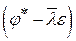 (т. к. (т. к.  ). По условию ). По условию  нормальный оператор, значит нормальный оператор, значит  . Нетрудно проверить, что . Нетрудно проверить, что
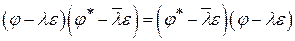 . .
Из того, что  является собственным вектором оператора является собственным вектором оператора  следует, что следует, что  , значит , значит

То есть  и и 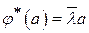 . □ . □
ТЕОРЕМА 2. Собственные векторы, соответствующие различным собственным значениям нормального оператора  будут ортогональны. будут ортогональны.
ДОКАЗАТЕЛЬСТВО. Пусть 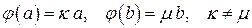 . .
Тогда
 . .
Откуда  , следовательно , следовательно  , т. к. , т. к.  . □ . □
ТЕОРЕМА 3. (основная о нормальных операторах). Для каждого нормального оператора  в унитарном пространстве в унитарном пространстве  найдётся ортонормированный базис, составленный из собственных векторов оператора найдётся ортонормированный базис, составленный из собственных векторов оператора  . Матрица . Матрица  имеет в этом базисе диагональный вид. имеет в этом базисе диагональный вид.
ДОКАЗАТЕЛЬСТВО. Пусть  характеристический корень линейного оператора характеристический корень линейного оператора  (по основной теореме алгебры комплексных чисел [3] такой корень существует). Ему соответствует собственный вектор (по основной теореме алгебры комплексных чисел [3] такой корень существует). Ему соответствует собственный вектор  . Рассмотрим множество . Рассмотрим множество  , которое является подпространством пространства , которое является подпространством пространства  и называется ортогональным к и называется ортогональным к  . Так как . Так как  , то для любого вектора , то для любого вектора  справедливо справедливо
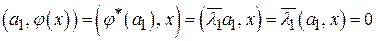 . .
Таким образом, 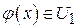 как только как только  . Такое подпространство называется инвариантным, относительно оператора . Такое подпространство называется инвариантным, относительно оператора  . .
Рассмотрим оператор 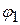 , заданный на , заданный на  следующим образом: следующим образом:  . Оно называется ограничением . Оно называется ограничением  на на  . Заметим, что собственные векторы . Заметим, что собственные векторы 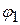 будут собственными векторами и будут собственными векторами и  . .
Далее аналогично находим в  собственный вектор собственный вектор  оператора оператора  . Пусть . Пусть  подпространство векторов, ортогональных к подпространство векторов, ортогональных к  и и  . .  будет опять инвариантным относительно будет опять инвариантным относительно  , т. к. является пересечением двух инвариантных подпространств. В нём снова найдётся собственный вектор , т. к. является пересечением двух инвариантных подпространств. В нём снова найдётся собственный вектор 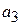 оператора оператора  . И т. д. . И т. д.
Продолжая указанную процедуру, получим ортогональный базис  пространства пространства  , составленный из собственных векторов оператора , составленный из собственных векторов оператора  . Остаётся нормировать этот базис. . Остаётся нормировать этот базис.
В этом базисе матрица линейного оператора будет иметь диагональный вид [2]. □
Унитарные операторы.
Линейный оператор  унитарного пространства унитарного пространства  называется унитарным, если он сохраняет скалярное произведение векторов, т. е. называется унитарным, если он сохраняет скалярное произведение векторов, т. е.
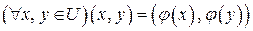 . .
Непосредственно из определения унитарного оператора следует:
 , ,
т. е.  тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого 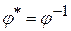 . .
Так как  , заключаем, что унитарный оператор является частным случаем нормального оператора. , заключаем, что унитарный оператор является частным случаем нормального оператора.
Если  матрица оператора матрица оператора  в некотором ортонормированном базисе, то матрица в некотором ортонормированном базисе, то матрица  будет будет  сопряжено транспонированной. Условие унитарности оператора сопряжено транспонированной. Условие унитарности оператора  в матричной форме будет выглядеть следующим образом: в матричной форме будет выглядеть следующим образом:  или или  . Такая матрица . Такая матрица  тоже называется унитарной. тоже называется унитарной.
Если линейный оператор рассматривается в евклидовом пространстве и сохраняет скалярное произведение, то его матрица в некотором базисе будет такой, что  , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу  ортогональной. ортогональной.
ТЕОРЕМА 1. Линейный оператор  унитарного пространства унитарного пространства  является унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е. является унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е.  . .
ДОКАЗАТЕЛЬСТВО. Действительно,
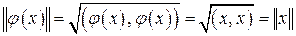 . .
В другую сторону, пусть  . Тогда для любого . Тогда для любого 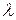 справедливо: справедливо:  . Если . Если  сохраняет скалярное произведение, то сохраняет скалярное произведение, то  . Раскрывая скобки и учитывая, что . Раскрывая скобки и учитывая, что  и и 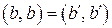 , получим , получим
 (1) (1)
При  получаем получаем
 (2) (2)
В случае евклидова пространства, т. к.  , имеем , имеем  . .
Иначе, положим в (1)  , получим , получим
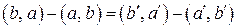 . .
Прибавим полученное равенство к (2), тогда  . □ . □
ТЕОРЕМА 2. Линейный оператор  унитарного пространства унитарного пространства  является унитарным тогда и только тогда, когда является унитарным тогда и только тогда, когда  переводит любой ортонормированный базис этого пространства снова в ортонормированный. переводит любой ортонормированный базис этого пространства снова в ортонормированный.
ДОКАЗАТЕЛЬСТВО. Пусть  ортонормированный базис пространства ортонормированный базис пространства  . По определению унитарного пространства . По определению унитарного пространства  , значит, , значит, 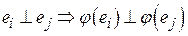 . А по предыдущей теореме . А по предыдущей теореме  . .
Обратно, пусть
 , ,  , тогда , тогда  . Так как по предположению . Так как по предположению  переводит ортонормированный базис в ортонормированный, то переводит ортонормированный базис в ортонормированный, то
 . .
Следовательно,  унитарный оператор. □ унитарный оператор. □
ТЕОРЕМА 3. (основная об унитарных операторах). Матрица унитарного оператора  в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице. в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице.
ДОКАЗАТЕЛЬСТВО. Так как  является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения  по модулю равны 1. по модулю равны 1.
Пусть 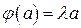 . тогда . тогда
 . .
Но 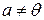 , т. е. , т. е. 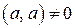 . Значит, . Значит,  , т. е. , т. е.  . □ . □
ЗАДАЧИ К ГЛАВЕ I.
1. Выяснить, являются ли ортогональными в евклидовом пространстве следующие системы векторов:
а) 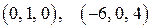 ; ;
б)  ; ;
в)  ; ;
г)  ; ;
д)  ? ?
2. Установить, образует ли каждая из указанных систем векторов ортогональный базис в евклидовом пространстве  : :
а)  ; ;
б)  ; ;
в)  ; ;
г)  ; ;
д)  ; ;
е)  ; ;
ж) 
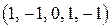 ? ?
3. Является ли нормированным каждый из векторов евклидова пространства  : :
а) 
б) 
в) 
г) 
д) 
е) 
ж) 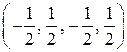 ? ?
4. Применяя процесс ортогонализации, по данному базису евклидова пространства  , построить ортонормированный: , построить ортонормированный:
а)  ; ;
б)  ; ;
в)  . .
5. Применяя процесс ортогонализации, по данному базису евклидова пространства 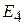 , построить ортонормированный: , построить ортонормированный:
а) 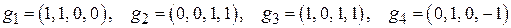 ; ;
б)  . .
6. Даны векторы евклидова пространства  . Найти длины векторов . Найти длины векторов  и и  , их скалярное произведение, косинус угла между ними: , их скалярное произведение, косинус угла между ними:
а)  ; ;
б)  ; ;
в) 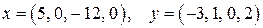 . .
7. Выяснить, является ли матрица  ортогональной, и если является, то найти обратную ей: ортогональной, и если является, то найти обратную ей:
а) 
б) 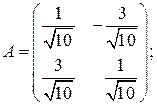
в) 
г) 
д) 
е) 
8. Какому условию должны удовлетворять  и и   , чтобы матрица , чтобы матрица  была ортогональной? была ортогональной?
9. Оператор  в некотором ортонормированном базисе задан матрицей в некотором ортонормированном базисе задан матрицей  . Выяснить, является ли оператор . Выяснить, является ли оператор  ортогональным, если: ортогональным, если:
а) 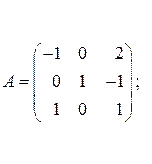
б) 
в) 
10. При каких условиях диагональная матрица будет ортогональной?
11. Оператор  имеет в некотором ортонормированном базисе матрицу имеет в некотором ортонормированном базисе матрицу  . Найти матрицу сопряжённого оператора . Найти матрицу сопряжённого оператора  в том же базисе, если: в том же базисе, если:
а) 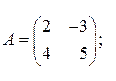
б) 
в) 
12. Оператор  имеет в некотором ортонормированном базисе матрицу имеет в некотором ортонормированном базисе матрицу  . Выяснить, является ли оператор . Выяснить, является ли оператор  самосопряжённым, если: самосопряжённым, если:
а) 
б) 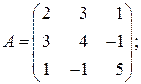
в) 
г) 
13. При каком значении  оператор, заданный матрицей оператор, заданный матрицей  в некотором ортонормированном базисе, является одновременно ортогональным и самосопряжённым, если: в некотором ортонормированном базисе, является одновременно ортогональным и самосопряжённым, если:
а) 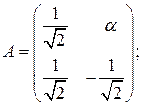
б) 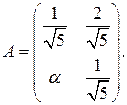
14. Линейный оператор  в некотором ортонормированном базисе в некотором ортонормированном базисе  имеет матрицу имеет матрицу  . Найти матрицу сопряжённого оператора . Найти матрицу сопряжённого оператора  в ортонормированном базисе в ортонормированном базисе  , если: , если:
а) 
б) 
в) 

Закон инерции.
Канонический вид, к которому приводится данная квадратичная форма, определяется неоднозначно. Всякая квадратичная форма может быть приведена к каноническому виду многими различными способами. Возникает вопрос, что общего у тех различных канонических квадратичных форм, к которым приводится данная форма  ? Этот вопрос тесно связан с другим вопросом: при каком условии одна из двух данных квадратичных форм может быть переведена в другую невырожденным линейным преобразованием? Ответ на эти вопросы, оказывается, зависит от того, рассматриваются ли комплексные или действительные квадратичные формы. ? Этот вопрос тесно связан с другим вопросом: при каком условии одна из двух данных квадратичных форм может быть переведена в другую невырожденным линейным преобразованием? Ответ на эти вопросы, оказывается, зависит от того, рассматриваются ли комплексные или действительные квадратичные формы.
Рассмотрим вначале произвольные комплексные квадратичные формы, допуская употребление невырожденных линейных преобразований также с произвольными комплексными коэффициентами. Известно, что всякая квадратичная форма  oт oт  неизвестных, имеющая ранг неизвестных, имеющая ранг  , приводится к каноническому виду , приводится к каноническому виду
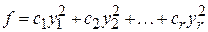 , ,
где все коэффициенты 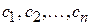 отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование: отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование:
 при при  ; ;  при при 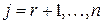 . .
Оно приводит форму  к виду к виду
 , (1) , (1)
называемому нормальным; это  просто сумма квадратов просто сумма квадратов  неизвестных с коэффициентами, равными единице. неизвестных с коэффициентами, равными единице.
Из равенства 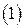 видно, что нормальный вид зависит лишь от ранга видно, что нормальный вид зависит лишь от ранга  формы формы  . Тогда, если формы . Тогда, если формы  и и  от от  неизвестных имеют одинаковый ранг неизвестных имеют одинаковый ранг  , то можно перевести , то можно перевести  в (1), а затем (1) в в (1), а затем (1) в  , т. к. преобразование, обратное невырожденному, также невырожденное. Таким образом, существует невырожденное линейное преобразование, переводящее , т. к. преобразование, обратное невырожденному, также невырожденное. Таким образом, существует невырожденное линейное преобразование, переводящее  в в  . Так как, с другой стороны, никакое невырожденное линейное преобразование не изменяет ранга формы, то мы приходим к следующему результату: . Так как, с другой стороны, никакое невырожденное линейное преобразование не изменяет ранга формы, то мы приходим к следующему результату:
ТЕОРЕМА 1. Две комплексные квадратичные формы от  неизвестных тогда и только тогда переводятся друг в друга невырожденными линейными преобразованиями с комплексными коэффициентами, если эти формы имеют один и тот же ранг. □ неизвестных тогда и только тогда переводятся друг в друга невырожденными линейными преобразованиями с комплексными коэффициентами, если эти формы имеют один и тот же ранг. □
Из этой теоремы без труда вытекает
СЛЕДСТВИЕ. Каноническим видом комплексной квадратичной формы ранга  может служить всякая сумма квадратов может служить всякая сумма квадратов  неизвестных с любыми отличными от нуля комплексными коэффициентами. □ неизвестных с любыми отличными от нуля комплексными коэффициентами. □
Иная ситуация в том случае, когда рассматриваются действительные квадратичные формы и допускаются лишь линейные преобразования с действительными коэффициентами. В этом случае уже не всякую форму можно привести к виду (1), так как это могло бы потребовать извлечения квадратного корня из отрицательного числа. Если, однако, мы назовем теперь нормальным видом квадратичной формы сумму квадратов нескольких неизвестных с коэффициентами  или или  , то легко показать, что всякую действительную квадратичную форму , то легко показать, что всякую действительную квадратичную форму  можно привести невырожденным линейным преобразованием с действительными, коэффициентами к нормальному виду. можно привести невырожденным линейным преобразованием с действительными, коэффициентами к нормальному виду.
В самом деле, форма  ранга ранга  от от  неизвестных приводится к каноническому виду, который можно записать следующим образом (меняя, если нужно, нумерацию неизвестных): неизвестных приводится к каноническому виду, который можно записать следующим образом (меняя, если нужно, нумерацию неизвестных):
 , ,  , ,
где все числа  отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами: отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами:
 при при 
| 


 и
и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие  , для которого
, для которого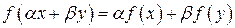 и
и  .
.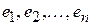 и
и  , соответственно, их ортонормированные базисы. Зададим отображение
, соответственно, их ортонормированные базисы. Зададим отображение  следующим образом: если
следующим образом: если ,
, .
. .
. и
и
 над полем
над полем 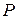 . Отображение
. Отображение  называется линейной функцией, если
называется линейной функцией, если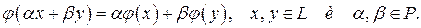
 линейные функции, то
линейные функции, то  и
и  , такие что
, такие что  и
и  , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в
, так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в  линейного пространства
линейного пространства  существует единственная линейная функция
существует единственная линейная функция  , такая, что
, такая, что .
. произвольный вектор из
произвольный вектор из  ,
,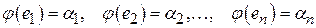 .
. линейная функция. Пусть
линейная функция. Пусть  . Тогда
. Тогда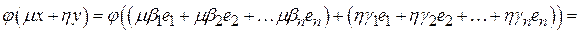


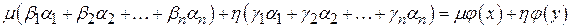 .
. , удовлетворяющая условию леммы, т. е.
, удовлетворяющая условию леммы, т. е. . Тогда
. Тогда  . □
. □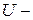 унитарное пространство. Положим по определению
унитарное пространство. Положим по определению  для любых
для любых 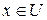 и фиксированного
и фиксированного 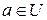 . Тогда имеет место
. Тогда имеет место . Обратно, для каждой линейной функции
. Обратно, для каждой линейной функции 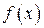 существует элемент
существует элемент  .
.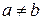 , тогда
, тогда  . При
. При  имеем
имеем  , т. е.
, т. е.  . Тем самым показано, что каждому
. Тем самым показано, что каждому  произвольная линейная функция, заданная в пространстве
произвольная линейная функция, заданная в пространстве  . Докажем, что существует элемент
. Докажем, что существует элемент  ортонормированный базис пространства
ортонормированный базис пространства  , такой, что
, такой, что  . Рассмотрим вектор
. Рассмотрим вектор ,
, . Для произвольного вектора
. Для произвольного вектора  , имеем
, имеем . □
. □ мерного унитарного пространства
мерного унитарного пространства  , сопряжённый данному. Выберем в
, сопряжённый данному. Выберем в  и рассмотрим функцию
и рассмотрим функцию  переменной
переменной  . Эта функция является линейной. Действительно
. Эта функция является линейной. Действительно
 . Оператор
. Оператор 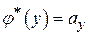 называется сопряжённым к
называется сопряжённым к 
 , тогда
, тогда 
 .
.
 .
. .
. ;
; ;
; ;
; .
. . Другие свойства доказываются аналогично.
. Другие свойства доказываются аналогично. квадратная матрица порядка
квадратная матрица порядка  , то матрица
, то матрица  , полученная из
, полученная из  заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если
заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если  , то
, то 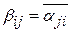 .
. , т. е. для любых
, т. е. для любых 
 ;
; .
. , получим
, получим , следовательно
, следовательно  матрицей
матрицей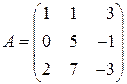 .
. заданы в некотором ортонормированном базисе
заданы в некотором ортонормированном базисе 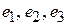 . Матрица перехода от
. Матрица перехода от  .
.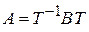 , где
, где  матрица того же оператора в ортонормированном базисе. Откуда
матрица того же оператора в ортонормированном базисе. Откуда  .
. .
. .
. .
.
 ,
, .
.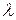 будет и собственным вектором оператора
будет и собственным вектором оператора  .
.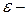 тождественный оператор
тождественный оператор  , то
, то  также линейный оператор, сопряжённым для которого будет
также линейный оператор, сопряжённым для которого будет 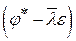 (т. к.
(т. к.  ). По условию
). По условию 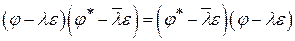 .
. , значит
, значит
 и
и 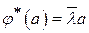 . □
. □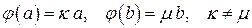 .
. .
. , следовательно
, следовательно  , т. к.
, т. к.  . □
. □ характеристический корень линейного оператора
характеристический корень линейного оператора  . Рассмотрим множество
. Рассмотрим множество  , которое является подпространством пространства
, которое является подпространством пространства  , то для любого вектора
, то для любого вектора  справедливо
справедливо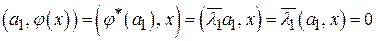 .
.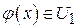 как только
как только  , заданный на
, заданный на  . Оно называется ограничением
. Оно называется ограничением  оператора
оператора  подпространство векторов, ортогональных к
подпространство векторов, ортогональных к  .
.  оператора
оператора  пространства
пространства 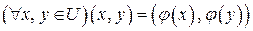 .
. ,
, тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого
тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого 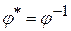 .
. , заключаем, что унитарный оператор является частным случаем нормального оператора.
, заключаем, что унитарный оператор является частным случаем нормального оператора. сопряжено транспонированной. Условие унитарности оператора
сопряжено транспонированной. Условие унитарности оператора  или
или  . Такая матрица
. Такая матрица  , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу
, т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу  ортогональной.
ортогональной. .
.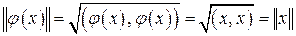 .
. . Тогда для любого
. Тогда для любого  . Если
. Если  . Раскрывая скобки и учитывая, что
. Раскрывая скобки и учитывая, что  и
и 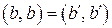 , получим
, получим (1)
(1) получаем
получаем (2)
(2) , имеем
, имеем  .
. , получим
, получим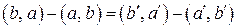 .
. , значит,
, значит, 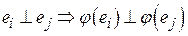 . А по предыдущей теореме
. А по предыдущей теореме  .
. ,
,  , тогда
, тогда  . Так как по предположению
. Так как по предположению  .
.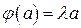 . тогда
. тогда .
.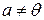 , т. е.
, т. е. 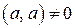 . Значит,
. Значит,  , т. е.
, т. е.  . □
. □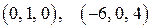 ;
; ;
; ;
; ;
; ?
? :
: ;
; ;
; ;
; ;
; ;
; ;
;
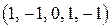 ?
?





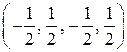 ?
? , построить ортонормированный:
, построить ортонормированный: ;
; ;
; .
.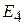 , построить ортонормированный:
, построить ортонормированный: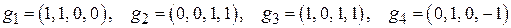 ;
; .
. ;
; ;
;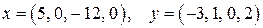 .
.
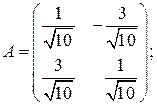




 и
и 
 , чтобы матрица
, чтобы матрица  была ортогональной?
была ортогональной? в некотором ортонормированном базисе задан матрицей
в некотором ортонормированном базисе задан матрицей 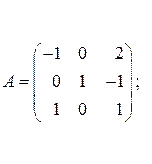


 имеет в некотором ортонормированном базисе матрицу
имеет в некотором ортонормированном базисе матрицу 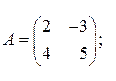



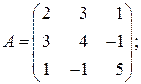


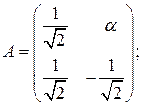
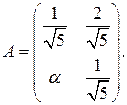
 , если:
, если:



 , приводится к каноническому виду
, приводится к каноническому виду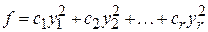 ,
,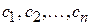 отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование:
отличны от нуля. Пользуясь тем, что из всякого комплексного числа извлекается квадратный корень, выполним следующее невырожденное линейное преобразование: при
при  ;
;  при
при 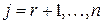 .
. , (1)
, (1)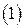 видно, что нормальный вид зависит лишь от ранга
видно, что нормальный вид зависит лишь от ранга  от
от  или
или  , то легко показать, что всякую действительную квадратичную форму
, то легко показать, что всякую действительную квадратичную форму  ,
,  ,
, отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами:
отличны от нуля и положительны. Тогда невырожденное линейное преобразование с действительными коэффициентами:


