Изоморфизм унитарных пространств.
Похожие статьи вашей тематики
Два унитарных (или евклидовых) пространства  и и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие  , для которого , для которого
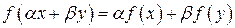 и и  . .
ТЕОРЕМА. (об изоморфизме унитарных пространств). Два унитарных пространства изоморфны тогда и только тогда, когда они имеют одинаковую размерность.
ДОКАЗАТЕЛЬСТВО. Очевидно, что если  и и  изоморфны, то они являются изоморфными, как линейные пространства. Однако изоморфные линейные пространства имеют одинаковую размерность [1]. изоморфны, то они являются изоморфными, как линейные пространства. Однако изоморфные линейные пространства имеют одинаковую размерность [1].
Обратно, пусть размерности  и и  равны, а равны, а 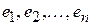 и и  , соответственно, их ортонормированные базисы. Зададим отображение , соответственно, их ортонормированные базисы. Зададим отображение  следующим образом: если следующим образом: если
 , ,
то считаем
 . .
Это отображение взаимнооднозначно и сохраняет операции сложения и умножения на число. Значит, они изоморфны, как линейные пространства.
Покажем, что  сохраняет скалярное произведение. Рассмотрим два произвольных вектора сохраняет скалярное произведение. Рассмотрим два произвольных вектора
 , ,
 . .
Тогда
 и и

То есть  . □ . □
Линейные функции.
Рассмотрим произвольное линейное пространство  над полем над полем 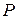 . Отображение . Отображение  называется линейной функцией, если называется линейной функцией, если
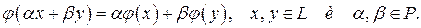
Нетрудно проверить, что если  и и  линейные функции, то линейные функции, то  и и  , такие что , такие что  и и  , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в  образуют линейное пространство относительно их сложения и умножения числа на функцию. образуют линейное пространство относительно их сложения и умножения числа на функцию.
ЛЕММА. (о существовании и единственности линейной функции). Для любого базиса  линейного пространства линейного пространства  и любого набора и любого набора  существует единственная линейная функция существует единственная линейная функция  , такая, что , такая, что
 . .
ДОКАЗАТЕЛЬСТВО. Пусть  произвольный вектор из произвольный вектор из  . Зададим отображение . Зададим отображение  следующим образом: следующим образом:
 , ,
Очевидно, что 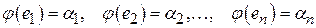 . .
Проверим, что  линейная функция. Пусть линейная функция. Пусть  . Тогда . Тогда
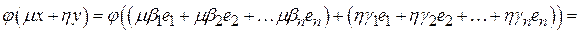


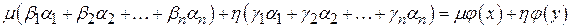 . .
Докажем единственность. Предположим, что существует другая линейная функция  , удовлетворяющая условию леммы, т. е. , удовлетворяющая условию леммы, т. е.
 . Тогда . Тогда  . □ . □
Пусть 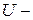 унитарное пространство. Положим по определению унитарное пространство. Положим по определению  для любых для любых 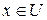 и фиксированного и фиксированного 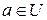 . Тогда имеет место . Тогда имеет место
ТЕОРЕМА. Функция  является линейной и однозначно определяется по является линейной и однозначно определяется по  . Обратно, для каждой линейной функции . Обратно, для каждой линейной функции 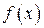 существует элемент существует элемент 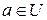 , такой что , такой что  . .
ДОКАЗАТЕЛЬСТВО. Вначале докажем линейность функции. Действительно
 . .
Пусть теперь 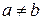 , тогда , тогда  . При . При  имеем имеем  , т. е. , т. е.  . Тем самым показано, что каждому . Тем самым показано, что каждому 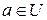 соответствует единственная линейная функция соответствует единственная линейная функция  . .
Наконец, пусть  произвольная линейная функция, заданная в пространстве произвольная линейная функция, заданная в пространстве  . Докажем, что существует элемент . Докажем, что существует элемент 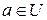 , такой, что , такой, что  для любых для любых 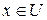 . Пусть . Пусть  ортонормированный базис пространства ортонормированный базис пространства  . По лемме, существует единственный набор . По лемме, существует единственный набор  , такой, что , такой, что  . Рассмотрим вектор . Рассмотрим вектор
 , ,
тогда  . Для произвольного вектора . Для произвольного вектора  , имеем , имеем
 . □ . □
Сопряжённые операторы.
Построим по каждому линейному оператору   мерного унитарного пространства мерного унитарного пространства  оператор оператор  , сопряжённый данному. Выберем в , сопряжённый данному. Выберем в  вектор вектор  и рассмотрим функцию и рассмотрим функцию  переменной переменной  . Эта функция является линейной. Действительно . Эта функция является линейной. Действительно

С другой стороны  , где , где 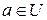 по теореме из предыдущего параграфа определяется однозначно по функции по теореме из предыдущего параграфа определяется однозначно по функции  , т. е. по , т. е. по  и и  . Таким образом, при фиксированном . Таким образом, при фиксированном  для каждого для каждого  имеется единственный вектор имеется единственный вектор  . Оператор . Оператор 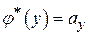 называется сопряжённым к называется сопряжённым к  , т. е. , т. е.

Покажем, что для каждого  сопряжённый оператор сопряжённый оператор  определяется однозначно. Предположим, что существует оператор определяется однозначно. Предположим, что существует оператор  , такой что , такой что  , тогда , тогда 
 . .
Нетрудно убедиться в том, что сопряжённый оператор  является линейным. Действительно является линейным. Действительно

 . .
Значит  . .
Отметим следующие свойства сопряжённого оператора:
1.  ; ;
2.  ; ;
3.  ; ;
4.  . .
Докажем первое свойство.
 . Другие свойства доказываются аналогично. . Другие свойства доказываются аналогично.
Если  квадратная матрица порядка квадратная матрица порядка  , то матрица , то матрица  , полученная из , полученная из  заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если  , то , то 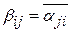 . .
ТЕОРЕМА. Если линейный оператор  в ортонормированном базисе имеет матрицу в ортонормированном базисе имеет матрицу  , то сопряжённый оператор , то сопряжённый оператор  будет иметь в этом базисе сопряжено транспонированную матрицу. будет иметь в этом базисе сопряжено транспонированную матрицу.
ДОКАЗАТЕЛЬСТВО. Пусть в унитарном пространстве  задан ортонормированный базис задан ортонормированный базис  , а матрицы операторов , а матрицы операторов  и и  в этом базисе будут соответственно в этом базисе будут соответственно  , т. е. для любых , т. е. для любых 
 ; ;
 . .
Домножим первое равенство справа на  , получим , получим
 , следовательно , следовательно 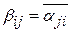 . □ . □
Пример 1. Линейный оператор  задан в евклидовом пространстве в базисе из векторов задан в евклидовом пространстве в базисе из векторов  матрицей матрицей
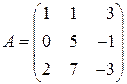 . .
Найти матрицу сопряжённого оператора  в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе. в том же базисе, считая, что координаты векторов базиса даны в некотором ортонормированном базисе.
Решение. Координаты векторов  заданы в некотором ортонормированном базисе заданы в некотором ортонормированном базисе 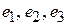 . Матрица перехода от . Матрица перехода от 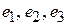 к к  будет будет
 . .
Значит, 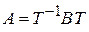 , где , где  матрица того же оператора в ортонормированном базисе. Откуда матрица того же оператора в ортонормированном базисе. Откуда  . .
Находим
 . .
Тогда
 . .
Матрица сопряжённого оператора  будет по предыдущей теореме сопряжено транспонированной, а так как оператор задан в евклидовом пространстве, то просто транспонированной. будет по предыдущей теореме сопряжено транспонированной, а так как оператор задан в евклидовом пространстве, то просто транспонированной.
 . .
Возвращаемся к исходному базису

Нормальные операторы.
Линейный оператор  унитарного пространства унитарного пространства  называется нормальным, если называется нормальным, если
 , ,
т. е. если он перестановочен со своим сопряжённым.
Если  ортонормированный базис пространства ортонормированный базис пространства  и и  матрица нормального оператора матрица нормального оператора  в этом базисе, то по теореме из §1.3 имеем в этом базисе, то по теореме из §1.3 имеем  . .
Справедливы следующие три теоремы о нормальных операторах.
ТЕОРЕМА 1. Всякий собственный вектор  нормального оператора нормального оператора  , соответствующий собственному значению , соответствующий собственному значению 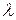 будет и собственным вектором оператора будет и собственным вектором оператора  , который соответствует комплексно-сопряжённому значению , который соответствует комплексно-сопряжённому значению  . .
ДОКАЗАТЕЛЬСТВО. Если  линейный оператор, а линейный оператор, а 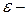 тождественный оператор тождественный оператор  , то , то  также линейный оператор, сопряжённым для которого будет также линейный оператор, сопряжённым для которого будет 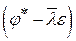 (т. к. (т. к.  ). По условию ). По условию  нормальный оператор, значит нормальный оператор, значит  . Нетрудно проверить, что . Нетрудно проверить, что
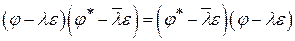 . .
Из того, что  является собственным вектором оператора является собственным вектором оператора  следует, что следует, что  , значит , значит

То есть  и и 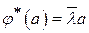 . □ . □
ТЕОРЕМА 2. Собственные векторы, соответствующие различным собственным значениям нормального оператора  будут ортогональны. будут ортогональны.
ДОКАЗАТЕЛЬСТВО. Пусть 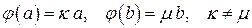 . .
Тогда
 . .
Откуда  , следовательно , следовательно  , т. к. , т. к.  . □ . □
ТЕОРЕМА 3. (основная о нормальных операторах). Для каждого нормального оператора  в унитарном пространстве в унитарном пространстве  найдётся ортонормированный базис, составленный из собственных векторов оператора найдётся ортонормированный базис, составленный из собственных векторов оператора  . Матрица . Матрица  имеет в этом базисе диагональный вид. имеет в этом базисе диагональный вид.
ДОКАЗАТЕЛЬСТВО. Пусть  характеристический корень линейного оператора характеристический корень линейного оператора  (по основной теореме алгебры комплексных чисел [3] такой корень существует). Ему соответствует собственный вектор (по основной теореме алгебры комплексных чисел [3] такой корень существует). Ему соответствует собственный вектор  . Рассмотрим множество . Рассмотрим множество  , которое является подпространством пространства , которое является подпространством пространства  и называется ортогональным к и называется ортогональным к  . Так как . Так как  , то для любого вектора , то для любого вектора  справедливо справедливо
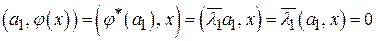 . .
Таким образом, 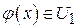 как только как только  . Такое подпространство называется инвариантным, относительно оператора . Такое подпространство называется инвариантным, относительно оператора  . .
Рассмотрим оператор 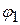 , заданный на , заданный на  следующим образом: следующим образом:  . Оно называется ограничением . Оно называется ограничением  на на  . Заметим, что собственные векторы . Заметим, что собственные векторы 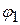 будут собственными векторами и будут собственными векторами и  . .
Далее аналогично находим в  собственный вектор собственный вектор  оператора оператора  . Пусть . Пусть  подпространство векторов, ортогональных к подпространство векторов, ортогональных к  и и  . .  будет опять инвариантным относительно будет опять инвариантным относительно  , т. к. является пересечением двух инвариантных подпространств. В нём снова найдётся собственный вектор , т. к. является пересечением двух инвариантных подпространств. В нём снова найдётся собственный вектор 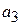 оператора оператора  . И т. д. . И т. д.
Продолжая указанную процедуру, получим ортогональный базис  пространства пространства  , составленный из собственных векторов оператора , составленный из собственных векторов оператора  . Остаётся нормировать этот базис. . Остаётся нормировать этот базис.
В этом базисе матрица линейного оператора будет иметь диагональный вид [2]. □
Унитарные операторы.
Линейный оператор  унитарного пространства унитарного пространства  называется унитарным, если он сохраняет скалярное произведение векторов, т. е. называется унитарным, если он сохраняет скалярное произведение векторов, т. е.
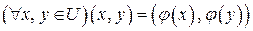 . .
Непосредственно из определения унитарного оператора следует:
 , ,
т. е.  тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого 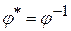 . .
Так как  , заключаем, что унитарный оператор является частным случаем нормального оператора. , заключаем, что унитарный оператор является частным случаем нормального оператора.
Если  матрица оператора матрица оператора  в некотором ортонормированном базисе, то матрица в некотором ортонормированном базисе, то матрица  будет будет  сопряжено транспонированной. Условие унитарности оператора сопряжено транспонированной. Условие унитарности оператора  в матричной форме будет выглядеть следующим образом: в матричной форме будет выглядеть следующим образом:  или или  . Такая матрица . Такая матрица  тоже называется унитарной. тоже называется унитарной.
Если линейный оператор рассматривается в евклидовом пространстве и сохраняет скалярное произведение, то его матрица в некотором базисе будет такой, что  , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу  ортогональной. ортогональной.
ТЕОРЕМА 1. Линейный оператор  унитарного пространства унитарного пространства  является унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е. является унитарным тогда и только тогда, когда он сохраняет длину вектора, т. е.  . .
ДОКАЗАТЕЛЬСТВО. Действительно,
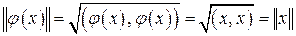 . .
В другую сторону, пусть  . Тогда для любого . Тогда для любого 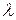 справедливо: справедливо:  . Если . Если  сохраняет скалярное произведение, то сохраняет скалярное произведение, то  . Раскрывая скобки и учитывая, что . Раскрывая скобки и учитывая, что  и и 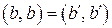 , получим , получим
 (1) (1)
При  получаем получаем
 (2) (2)
В случае евклидова пространства, т. к.  , имеем , имеем  . .
Иначе, положим в (1)  , получим , получим
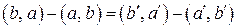 . .
Прибавим полученное равенство к (2), тогда  . □ . □
ТЕОРЕМА 2. Линейный оператор  унитарного пространства унитарного пространства  является унитарным тогда и только тогда, когда является унитарным тогда и только тогда, когда  переводит любой ортонормированный базис этого пространства снова в ортонормированный. переводит любой ортонормированный базис этого пространства снова в ортонормированный.
ДОКАЗАТЕЛЬСТВО. Пусть  ортонормированный базис пространства ортонормированный базис пространства  . По определению унитарного пространства . По определению унитарного пространства  , значит, , значит, 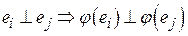 . А по предыдущей теореме . А по предыдущей теореме  . .
Обратно, пусть
 , ,  , тогда , тогда  . Так как по предположению . Так как по предположению  переводит ортонормированный базис в ортонормированный, то переводит ортонормированный базис в ортонормированный, то
 . .
Следовательно,  унитарный оператор. □ унитарный оператор. □
ТЕОРЕМА 3. (основная об унитарных операторах). Матрица унитарного оператора  в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице. в подходящем ортонормированном базисе является диагональной, с диагональными элементами, равными по модулю единице.
ДОКАЗАТЕЛЬСТВО. Так как  является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения является частным случаем нормального оператора, то по основной теореме о нормальных операторах, в некотором ортонормированном базисе он задаётся диагональной матрицей. Покажем, что собственные значения  по модулю равны 1. по модулю равны 1.
Пусть 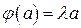 . тогда . тогда
 . .
Но 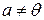 , т. е. , т. е. 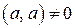 . Значит, . Значит,  , т. е. , т. е.  . □ . □
|



 и
и  называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие
называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие  , для которого
, для которого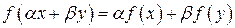 и
и  .
. и
и  , соответственно, их ортонормированные базисы. Зададим отображение
, соответственно, их ортонормированные базисы. Зададим отображение  следующим образом: если
следующим образом: если ,
, .
. .
. и
и
 над полем
над полем 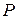 . Отображение
. Отображение  называется линейной функцией, если
называется линейной функцией, если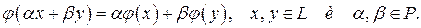
 линейные функции, то
линейные функции, то  и
и  , такие что
, такие что  и
и  , так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в
, так же являются линейными функциями. Поэтому, множество всех линейных функций, заданных в  линейного пространства
линейного пространства  существует единственная линейная функция
существует единственная линейная функция  , такая, что
, такая, что .
. произвольный вектор из
произвольный вектор из  ,
,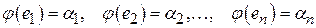 .
. линейная функция. Пусть
линейная функция. Пусть  . Тогда
. Тогда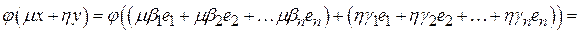


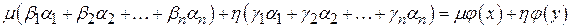 .
. , удовлетворяющая условию леммы, т. е.
, удовлетворяющая условию леммы, т. е. . Тогда
. Тогда  . □
. □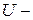 унитарное пространство. Положим по определению
унитарное пространство. Положим по определению  для любых
для любых 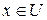 и фиксированного
и фиксированного 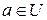 . Тогда имеет место
. Тогда имеет место . Обратно, для каждой линейной функции
. Обратно, для каждой линейной функции 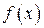 существует элемент
существует элемент  .
.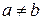 , тогда
, тогда  . При
. При  имеем
имеем  , т. е.
, т. е.  . Тем самым показано, что каждому
. Тем самым показано, что каждому  произвольная линейная функция, заданная в пространстве
произвольная линейная функция, заданная в пространстве  . Докажем, что существует элемент
. Докажем, что существует элемент  ортонормированный базис пространства
ортонормированный базис пространства  , такой, что
, такой, что  . Рассмотрим вектор
. Рассмотрим вектор ,
, . Для произвольного вектора
. Для произвольного вектора  , имеем
, имеем . □
. □ мерного унитарного пространства
мерного унитарного пространства  , сопряжённый данному. Выберем в
, сопряжённый данному. Выберем в  и рассмотрим функцию
и рассмотрим функцию  переменной
переменной  . Эта функция является линейной. Действительно
. Эта функция является линейной. Действительно
 . Оператор
. Оператор 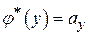 называется сопряжённым к
называется сопряжённым к 
 , тогда
, тогда 
 .
.
 .
. .
. ;
; ;
; ;
; .
. . Другие свойства доказываются аналогично.
. Другие свойства доказываются аналогично. квадратная матрица порядка
квадратная матрица порядка  , то матрица
, то матрица  , полученная из
, полученная из  заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если
заменой всех её элементов на комплексно-сопряжённые и последующим её транспонированием, называется сопряжено транспонированной. Т. е. если  , то
, то 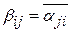 .
. , т. е. для любых
, т. е. для любых 
 ;
; .
. , получим
, получим , следовательно
, следовательно  матрицей
матрицей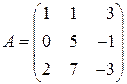 .
. заданы в некотором ортонормированном базисе
заданы в некотором ортонормированном базисе 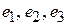 . Матрица перехода от
. Матрица перехода от  .
.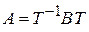 , где
, где  матрица того же оператора в ортонормированном базисе. Откуда
матрица того же оператора в ортонормированном базисе. Откуда  .
. .
. .
. .
.
 ,
, .
.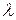 будет и собственным вектором оператора
будет и собственным вектором оператора  .
.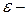 тождественный оператор
тождественный оператор  , то
, то  также линейный оператор, сопряжённым для которого будет
также линейный оператор, сопряжённым для которого будет 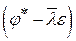 (т. к.
(т. к.  ). По условию
). По условию 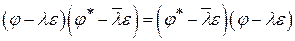 .
. , значит
, значит
 и
и 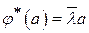 . □
. □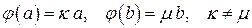 .
. .
. , следовательно
, следовательно  , т. к.
, т. к.  . □
. □ характеристический корень линейного оператора
характеристический корень линейного оператора  . Рассмотрим множество
. Рассмотрим множество  , которое является подпространством пространства
, которое является подпространством пространства  , то для любого вектора
, то для любого вектора  справедливо
справедливо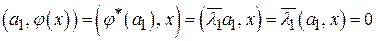 .
.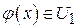 как только
как только  , заданный на
, заданный на  . Оно называется ограничением
. Оно называется ограничением  оператора
оператора  подпространство векторов, ортогональных к
подпространство векторов, ортогональных к  .
.  оператора
оператора  пространства
пространства 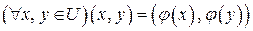 .
. ,
, тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого
тождественный оператор. Следовательно, унитарный оператор можно определить как оператор, для которого 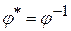 .
. , заключаем, что унитарный оператор является частным случаем нормального оператора.
, заключаем, что унитарный оператор является частным случаем нормального оператора. сопряжено транспонированной. Условие унитарности оператора
сопряжено транспонированной. Условие унитарности оператора  или
или  . Такая матрица
. Такая матрица  , т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу
, т. е. транспонированная матрица совпадает с обратной. Такой оператор называют ортогональным, а его матрицу  ортогональной.
ортогональной. .
.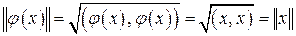 .
. . Тогда для любого
. Тогда для любого  . Если
. Если  . Раскрывая скобки и учитывая, что
. Раскрывая скобки и учитывая, что  и
и 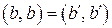 , получим
, получим (1)
(1) получаем
получаем (2)
(2) , имеем
, имеем  .
. , получим
, получим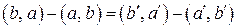 .
. , значит,
, значит, 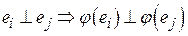 . А по предыдущей теореме
. А по предыдущей теореме  .
. ,
,  , тогда
, тогда  . Так как по предположению
. Так как по предположению  .
.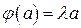 . тогда
. тогда .
.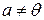 , т. е.
, т. е. 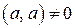 . Значит,
. Значит,  , т. е.
, т. е.  . □
. □


