
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операторы в евклидовом пространстве.Содержание книги
Поиск на нашем сайте Как уже отмечалось в §1.4 (теорема 3), в унитарном пространстве всякий линейный оператор имеет собственный вектор (одномерное инвариантное подпространство). В случае евклидова пространства это утверждение неверно. Однако имеет место следующая ТЕОРЕМА 1. У всякого линейного оператора ДОКАЗАТЕЛЬСТВО. Выберем в Рассмотрим систему уравнений
и будем искать для нее ненулевое решение
равен нулю. Приравняв его нулю, мы получим уравнение a)
или т. е. b)
есть решение системы (1), подставляя эти числа вместо
и соответственно
Будем теперь
Равенства (3) означают, что двумерное подпространство, порожденное векторами Если потребовать в доказательстве теоремы, чтобы базис
будут ортогональными (теорема 2 §1.4). Тогда Докажем теперь, что подпространство векторов
Аналогично, Рассмотрим ограничение
Представляя комплексное число
Таким образом, оператор
Первый из которых соответствует преобразованию подобия с центром в начале координат и коэффициентом растяжения ТЕОРЕМА 2. (основная о нормальных операторах в евклидовых пространствах). Матрица нормального оператора ДОКАЗАТЕЛЬСТВО. Оно аналогично доказательству теоремы 3 §1.4 о нормальных операторах. Отличие состоит в том, что мы не можем утверждать, что характеристический многочлен Так как пространство векторов, ортогональных векторам ТЕОРЕМА 3. (основная об ортогональных операторах в евклидовых пространствах). В подходящем ортонормированном базисе матрица ортогонального оператора клеточно-диагональная с клетками порядка 1 и 2; причём в клетках порядка 1 содержатся числа 1 или -1, а клетки порядка 2 имеют вид ДОКАЗАТЕЛЬСТВО. Оно следует из теоремы 2 о нормальных операторах в евклидовых пространствах и того факта, что собственные значения ортогонального оператора (как частного случая унитарного оператора) по модулю равны 1. Действительно, если модули собственных значений чисел Пример 3. Рассмотрим трёхмерное евклидово пространство
Операторы соответствуют следующим преобразованиям пространства: a) тождественное преобразование; b) зеркальное отображение относительно плоскости c) зеркальное отображение относительно прямой d) зеркальное отображение относительно точки e) вращение на угол f) вращение на угол Для симметрических операторов теорема формулируется так же, как и для эрмитовых. Согласно теореме 2 данного параграфа матрица оператора ТЕОРЕМА 4. (основная о симметрических операторах). Матрица симметрического оператора в подходящем ортонормированном базисе является диагональной с действительными числами по главной диагонали. □ ТЕОРЕМА 5. (основная о кососимметрических операторах в евклидовых пространствах). В подходящем ортонормированном базисе матрица кососимметрического оператора евклидова пространства имеет клеточно-диагональный вид с клетками порядков 1 или 2; причём в клетках порядка 1 находится число 0, а клетки порядка 2 имеют вид ДОКАЗАТЕЛЬСТВО следует из теоремы 2 о нормальных операторах в евклидовых пространствах и того факта, что собственные значения кососимметрического оператора либо 0, либо чисто мнимое число. □ ЗАДАЧИ К ГЛАВЕ I. 1. Выяснить, являются ли ортогональными в евклидовом пространстве следующие системы векторов: а) б) в) г) д) 2. Установить, образует ли каждая из указанных систем векторов ортогональный базис в евклидовом пространстве а) б) в) г) д) е) ж)
3. Является ли нормированным каждый из векторов евклидова пространства а) б) в) г) д) е) ж)
4. Применяя процесс ортогонализации, по данному базису евклидова пространства а) б) в) 5. Применяя процесс ортогонализации, по данному базису евклидова пространства а) б) 6. Даны векторы евклидова пространства а) б) в) 7. Выяснить, является ли матрица а) б) в) г)
д) е) 8. Какому условию должны удовлетворять 9. Оператор а) б) в) 10. При каких условиях диагональная матрица будет ортогональной? 11. Оператор а) б) в) 12. Оператор а) б) в) г) 13. При каком значении а) б) 14. Линейный оператор а) б)
в)
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 в евклидовом пространстве
в евклидовом пространстве  существует одномерное или двумерное инвариантное подпространство.
существует одномерное или двумерное инвариантное подпространство. . Оператору
. Оператору  .
. (1)
(1) . Такое решение существует тогда и только тогда, когда определитель
. Такое решение существует тогда и только тогда, когда определитель
 ой степени относительно
ой степени относительно 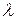 с действительными коэффициентами. Пусть
с действительными коэффициентами. Пусть  есть корень этого уравнения. Возможны два случая:
есть корень этого уравнения. Возможны два случая: в базисе
в базисе  (где
(где  столбец из координат вектора
столбец из координат вектора  ,
, , т. е.
, т. е. 
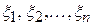 в (1) и отделяя вещественную часть от мнимой, получим:
в (1) и отделяя вещественную часть от мнимой, получим: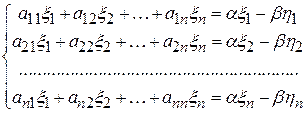 (2)
(2) (2')
(2') ) считать координатами некоторого вектора
) считать координатами некоторого вектора  ) в
) в 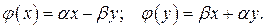 (3)
(3) собственное значение, то и
собственное значение, то и  также будет собственным значением (как корни многочлена с действительными коэффициентами). Соответствующие собственные векторы
также будет собственным значением (как корни многочлена с действительными коэффициентами). Соответствующие собственные векторы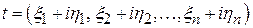 ,
, 
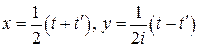 . Следовательно,
. Следовательно,  .
. , ортогональных векторам
, ортогональных векторам  , т. е.
, т. е. 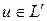 , то
, то .
. .
.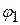 оператора
оператора  оператора
оператора  будет:
будет: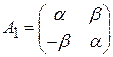 .
. , придадим матрице
, придадим матрице  .
. 
 и
и  .
. ; второй
; второй  поворот в плоскости
поворот в плоскости  около начала координат.
около начала координат. , которые по теореме 1 позволяют определить подпространство размерности 2, инвариантное относительно
, которые по теореме 1 позволяют определить подпространство размерности 2, инвариантное относительно  ,
,  .
. и клетка
и клетка  . По теореме 3 для каждого ортогонального оператора
. По теореме 3 для каждого ортогонального оператора 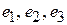 , что матрица оператора
, что матрица оператора 

 ;
; ;
; ;
; ;
; .
.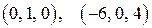 ;
; ;
; ;
; ;
; ?
? :
: ;
; ;
; ;
; ;
; ;
; ;
;
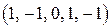 ?
?





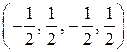 ?
? , построить ортонормированный:
, построить ортонормированный: ;
; ;
; .
.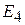 , построить ортонормированный:
, построить ортонормированный: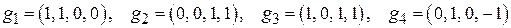 ;
; .
. ;
; ;
;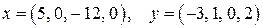 .
. ортогональной, и если является, то найти обратную ей:
ортогональной, и если является, то найти обратную ей:
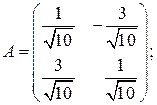




 и
и 
 , чтобы матрица
, чтобы матрица  была ортогональной?
была ортогональной? в некотором ортонормированном базисе задан матрицей
в некотором ортонормированном базисе задан матрицей 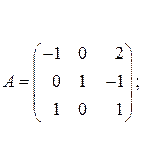


 имеет в некотором ортонормированном базисе матрицу
имеет в некотором ортонормированном базисе матрицу  в том же базисе, если:
в том же базисе, если: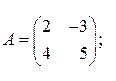



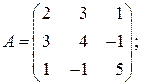


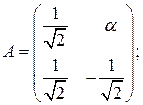
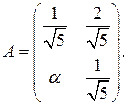
 , если:
, если:






