
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь подобия числовых матриц сСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эквивалентностью их характеристических матриц.
Как известно [1], две квадратные матрицы порядка ТЕОРЕМА. Матрицы ДОКАЗАТЕЛЬСТВО. Пусть матрицы
Тогда
Невырожденные числовые матрицы Обратно, пусть
Тогда существуют такие унимодулярные матрицы
Учитывая, что для унимодулярных матриц обратные матрицы существуют и являются
Так как
Аналогично
Используя (3) и (4) и учитывая (1), получаем:
или, применяя (2),
Квадратная скобка, стоящая справа, равна в действительности нулю: в противном случае она, являясь Таким образом,
откуда, приравнивая матричные коэффициенты при одинаковых степенях
Равенство (6) показывает, что числовая матрица
а тогда равенство (5) принимает вид
что и доказывает подобие матриц Пример 3. Являются ли следующие матрицы подобными
Решение. Их характеристические матрицы эквивалентны, так как приводятся к одному и тому же каноническому виду
поэтому матрицы
Жорданова нормальная форма. В этом параграфе будем рассматривать квадратные матрицы порядка Будет выделен один специальный тип матриц, так называемые жордановы матрицы, и будет показано, что эти матрицы служат нормальной формой для весьма широкого класса матриц. Именно, матрицы, все характеристические корни которых лежат в основном поле Введем необходимые определения. Жордановой клеткой порядка
иными словами, на ее главной диагонали стоит одно и то же число
будут соответственно жордановыми клетками первого, второго и третьего порядков. Жордановой матрицей порядка
вдоль главной диагонали которой расположены жордановы клетки
Строение жордановой матрицы можно также описать, не прибегая к понятию жордановой клетки. Именно, матрица
где Очевидно следующее УТВЕРЖДЕНИЕ. Диагональные матрицы являются частным случаем жордановых матриц, это будут в точности те жордановы матрицы, у которых все жордановы клетки имеют порядок Найдём канонический вид для характеристической матрицы ЛЕММА 1. Каноническим видом для характеристической матрицы одной жордановой клетки порядка
служит следующая
ДОКАЗАТЕЛЬСТВО. Вычисляя определитель этой матрицы, и вспоминая, что старший коэффициент многочлена
С другой стороны, среди миноров
ЛЕММА 2. Если многочлены
ДОКАЗАТЕЛЬСТВО. Рассмотрим случай
Поэтому
Далее применим индукцию по Теперь укажем практический метод нахождения канонического вида характеристической матрицы
для жордановой матрицы
Тогда, очевидно
Применяя элементарные преобразования к тем строкам и столбцам матрицы (5), которые проходят через клетку
При этом мы не указываем те места на диагонали, на которых стоят многочлены (7), так как в любой диагональной Пусть
если при этом в Проделав это для
Это и будет искомый канонический вид матрицы
Пример 4. Найти инвариантные множители характеристической матрицы для следующей жордановой:
Решение. Составим таблицу многочленов (7):
Поэтому инвариантными множителями матрицы
в то время как ТЕОРЕМА. Две жордановы матрицы тогда и только тогда подобны, когда они состоят из одних и тех же жордановых клеток, т. е. отличаются, быть может, лишь расположением этих клеток вдоль главной диагонали. ДОКАЗАТЕЛЬСТВО. В самом деле, таблица многочленов (7) полностью определяется набором жордановых клеток жордановой матрицы Обратно, если жордановы матрицы СЛЕДСТВИЕ. Жорданова матрица, подобная диагональной матрице, сама диагональна; две диагональные матрицы тогда и только тогда подобны, если получаются друг из друга перестановкой чисел, стоящих на главной диагонали. □
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.96.249 (0.013 с.) |

 подобны тогда и только тогда, когда они задают один и тот же линейный оператор в разных базисах. Однако мы не можем пока ответить на вопрос, подобны ли данные числовые матрицы
подобны тогда и только тогда, когда они задают один и тот же линейный оператор в разных базисах. Однако мы не можем пока ответить на вопрос, подобны ли данные числовые матрицы  и
и 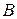 (т. е. матрицы с элементами из основного поля
(т. е. матрицы с элементами из основного поля 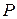 ). Тем не менее, их характеристические матрицы
). Тем не менее, их характеристические матрицы  и
и  являются
являются  матрицами, и вопрос об эквивалентности этих матриц решается вполне эффективно. Ответ на вопрос о связи подобия числовых матриц с эквивалентностью их характеристических матриц даёт следующая
матрицами, и вопрос об эквивалентности этих матриц решается вполне эффективно. Ответ на вопрос о связи подобия числовых матриц с эквивалентностью их характеристических матриц даёт следующая , что
, что .
. .
. и
и  .
. и
и 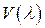 , что
, что . (1)
. (1) (2)
(2)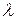 степень
степень 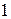 , причем старшим коэффициентом соответствующего матричного многочлена служит невырожденная матрица
, причем старшим коэффициентом соответствующего матричного многочлена служит невырожденная матрица  , то к матрицам
, то к матрицам  и
и  , причём, степень
, причём, степень  , равна
, равна  по
по  . (3)
. (3)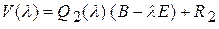 . (4)
. (4)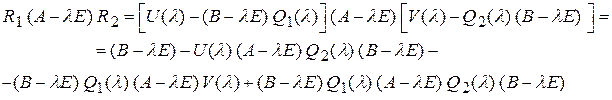

 и
и  есть
есть  . Это, однако, невозможно, так как слева стоит
. Это, однако, невозможно, так как слева стоит  ,
, , (5)
, (5)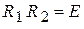 . (6)
. (6) не только отлична от нуля, но даже является невырожденной, причем
не только отлична от нуля, но даже является невырожденной, причем ,
, ,
, ,
,  ?
? ,
, , относящейся к числу
, относящейся к числу  , называется матрица порядка
, называется матрица порядка  , имеющая вид
, имеющая вид (1)
(1)
 (2)
(2) некоторых порядков, не обязательно различных, относящиеся к некоторым числам из поля
некоторых порядков, не обязательно различных, относящиеся к некоторым числам из поля  , т. е. одна жорданова клетка порядка
, т. е. одна жорданова клетка порядка  .
. будет жордановой матрицей тогда и только тогда, когда она имеет вид
будет жордановой матрицей тогда и только тогда, когда она имеет вид ,
, произвольные числа из поля
произвольные числа из поля  равно либо единице, либо нулю, причем, если
равно либо единице, либо нулю, причем, если  , то
, то  .
. произвольной жордановой матрицы
произвольной жордановой матрицы  (3)
(3) . (4)
. (4) должен равняться
должен равняться  .
. го порядка матрицы (3) имеется минор, равный единице, а именно тот, который получается после вычеркивания первого столбца и последней строки этой матрицы. Поэтому
го порядка матрицы (3) имеется минор, равный единице, а именно тот, который получается после вычеркивания первого столбца и последней строки этой матрицы. Поэтому . □
. □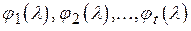 из кольца
из кольца 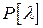 попарно взаимно просты, то имеет место следующая эквивалентность:
попарно взаимно просты, то имеет место следующая эквивалентность: .
. . Так как многочлены
. Так как многочлены 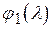 и
и 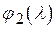 взаимно просты, то в кольце
взаимно просты, то в кольце  и
и  что
что .
.
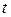 . □
. □ (5)
(5) есть единичная матрица того же порядка, что и клетка
есть единичная матрица того же порядка, что и клетка  . Пусть жордановы клетки матрицы
. Пусть жордановы клетки матрицы  , где
, где  . Пусть, далее, к числу
. Пусть, далее, к числу  ,
,  относится
относится 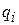 жордановых клеток,
жордановых клеток, 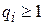 , и пусть порядки этих клеток, расположенные в невозрастающем порядке, будут
, и пусть порядки этих клеток, расположенные в невозрастающем порядке, будут . (6)
. (6) .
. этой матрицы, мы не будем затрагивать, очевидно, других диагональных клеток. Отсюда следует, что в матрице (5) можно при помощи элементарных преобразований заменить каждую клетку
этой матрицы, мы не будем затрагивать, очевидно, других диагональных клеток. Отсюда следует, что в матрице (5) можно при помощи элементарных преобразований заменить каждую клетку  , соответствующей клеткой вида (4). Иными словами, матрица
, соответствующей клеткой вида (4). Иными словами, матрица 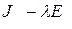 эквивалентна диагональной матрице, на диагонали которой стоят, помимо некоторого числа единиц, также следующие многочлены, соответствующие всем жордановым клеткам матрицы
эквивалентна диагональной матрице, на диагонали которой стоят, помимо некоторого числа единиц, также следующие многочлены, соответствующие всем жордановым клеткам матрицы  (7)
(7)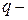 наибольшее среди чисел
наибольшее среди чисел  . Обозначим через
. Обозначим через  произведение многочленов, стоящих в
произведение многочленов, стоящих в  ом столбце таблицы (7),
ом столбце таблицы (7),  т.е.
т.е.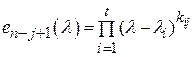 ; (8)
; (8)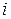 может оказаться, что
может оказаться, что  ), то соответствующие множители в (8) считаем равными единице. Так как числа
), то соответствующие множители в (8) считаем равными единице. Так как числа  по условию различные, то степени линейных двучленов, стоящие в
по условию различные, то степени линейных двучленов, стоящие в  (9)
(9) .
.

 .
. обладают одним и тем же набором жордановых клеток, то им соответствует одна и та же таблица многочленов (7), а поэтому одни и те же многочлены (8). Таким образом, характеристические матрицы
обладают одним и тем же набором жордановых клеток, то им соответствует одна и та же таблица многочленов (7), а поэтому одни и те же многочлены (8). Таким образом, характеристические матрицы  обладают одинаковыми инвариантными множителями, т. е. эквивалентны, а поэтому сами матрицы
обладают одинаковыми инвариантными множителями, т. е. эквивалентны, а поэтому сами матрицы  будут те из этих инвариантных множителей, которые отличны от единицы. Однако по многочленам (8) восстанавливается таблица многочленов (7). Именно, многочлены (8) разлагаются в произведение степеней линейных множителей, так как этим свойством обладают, как уже доказано, инвариантные множители характеристической матрицы для любой жордановой матрицы. Таблица (7) как раз и состоит из всех тех максимальных степеней линейных множителей, на которые разлагаются многочлены (8). Наконец, по таблице (7) восстанавливаются жордановы клетки исходных жордановых матриц: каждому многочлену
будут те из этих инвариантных множителей, которые отличны от единицы. Однако по многочленам (8) восстанавливается таблица многочленов (7). Именно, многочлены (8) разлагаются в произведение степеней линейных множителей, так как этим свойством обладают, как уже доказано, инвариантные множители характеристической матрицы для любой жордановой матрицы. Таблица (7) как раз и состоит из всех тех максимальных степеней линейных множителей, на которые разлагаются многочлены (8). Наконец, по таблице (7) восстанавливаются жордановы клетки исходных жордановых матриц: каждому многочлену  из таблицы (7) соответствует жорданова клетка порядка
из таблицы (7) соответствует жорданова клетка порядка  , относящаяся к числу
, относящаяся к числу  . Этим доказано, что матрицы
. Этим доказано, что матрицы 


