
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матриці. Означення. Види матрицьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Означення 1. Матрицею розміру
Скорочено пишуть
числа Означення 2. Дві матриці А і В однакових розмірів
Розглянемо основні види матриць. Нульовою називається матриця Квадратною називається матриця, в якої кількість рядків дорівнює кількості стовпців Діагональною називається така квадратна матриця, в якої елементи головної діагоналі відмінні від нуля, а всі решта елементів дорівнюють нулю, позначається
Діагональна матриця, в якої всі діагональні елементи дорівнюють одиниці, називається одиничною матрицею, і позначається
Матриця що складається з одного стовпця називається матрицею-стовпцем
Аналогічно, матриця-рядок складається з одного рядка
Звернемо увагу, що ряд факторів пов’язаних з поняттям матриці для багатьох так чи інакше могли бути відомими ще до знайомства з самим терміном. Розглянемо приклади. Приклад 1. Відомість на отримання стипендії для 20 студентів є прикладом матриці розміром 20х1, елементами якої є розмір стипендії кожному. Приклад 2. У відомості на зарплату бригаді для 15 робітників можуть бути вказані суми: нарахована, утримана і до оплати. Дані цієї відомості теж представляють матрицю розміру 15х3. Приклад 3. При виконанні робіт в шахті (метро, тунелі) по проходці можна виділити два основних види робіт: виїмка породи (сюди входить буріння шпурів, заряжання, зривання, прибирання породи) і кріплення. Обидва види робіт при сталій площі поперечного перетину можуть вимірюватись в погонних метрах. Припустимо, що протягом доби кожна із трьох змін добилися таких результатів:
Ці результати можна записати у вигляді матриці розміром 3х2:
Лінійні дії над матрицями
Іноді в роботі з таблицями (матрицями) прикладів типу 1–3 із 1.8., доводиться виконувати над ними певні операції. Так, якщо в прикладі 1 потрібно підрахувати заплановий розмір стипендій за семестр (6 місяців), то очевидно необхідно кожний елемент цієї матриці помножити на 6. Виникає необхідність множити матрицю на число. Якщо в умовах прикладу 2 ми маємо відомості 3-х місяців одного квартала, то можна скласти зведену відомість за квартал, додаючи розміщені у відповідних графах дані стосовно кожного робітника. Приходимо до дії додавання матриць. Якщо в умовах прикладу 3, 1.8. позначити через
Отже з прикладів бачимо, що цілком природно виникає необхідність дій множення матриці на число і додавання матриць. Означення 1. Добутком числа
Матриця (–1) Дія додавання вводиться тільки для матриць одного і того ж розміру. Означення 2. Сумою двох матриць Якщо ж Дії додавання, віднімання і множення матриць на число називаються лінійними діями над матрицями. Можна перевірити, що вони мають такі властивості:
Тут позначено через 0 – нульову матрицю і Вправа. Перевірити властивості 1–8 для матриць
і чисел Приклад. Задані матриці
Знайти 1) Розв’язання. 1)
2) Множення матриць
Множення матриць розглянемо, починаючи з відомого вже прикладу 3, при підрахунку грошових затрат на виконання робіт по проходці в шахті (метро, тунелі). Нехай в рядках матриці
записані результати роботи за добу кожної із трьох змін: по виїмці породи (перший стовпець) і по кріпленню пройденої виробки (другий стовпець). Як вже згадувалось, при заданій площі поперечного перетину проходки результати робіт можуть вимірюватись в пройденних погонних метрах. Замовнику необхідно знати, яку суму грошей прийдеться виділяти на оплату праці робітників, а яку – на капітальні витрати. Існують норми розцінок на зарплату і капітальні витрати, які представимо у вигляді матриці розцінок
де перший стовпець Загальні затрати на зарплату для кожної із змін дорівнюють сумі добутків пройдених кількостей метрів по обох видах робіт на відповідні норми розцінок. Позначимо через
Отримаємо таблицю затрат
Ці дані запишемо у вигляді нової матриці затрат
Для множення матриці Означення 1. Добутком матриці
Із структури елементів Приклад 1. Знайти добуток матриць Розв’язання. Матриця
Приклад 2. Переконатись, що для даних матриць
Звернути увагу, що в даному випадку Приклад 3. Переконатись, що для даних матриць
Звернути увагу, що добуток двох ненульових матриць може давати нульову матрицю, і, крім того, Означення 2. Матриці Приклад 4.
Легко перевірити, що довільна квадратна і одинична матриці комутативні, і при цьому Приклад 5. Перевірити останню рівність, якщо
Можна показати, що множення матриць має такі властивості:
Тут мається на увазі, що всі записані добутки матриць існують. Приклад 6. Перевірити властивості 1-4, якщо число
Розглянемо поняття степеня квадратної матриці. Означення 3. Квадратом матриці Аналогічно вводиться Приклад 7. Для матриць
довести, що Означення 4. Якщо
де Приклад 8. Для матриці
Знайти Обчислити степені квадратних матриць: 9. 12. Перемножити прямокутні матриці: 15. 17. Знайти
Відповіді.
10. 13. 16.
Визначник добутку матриць
Визначник квадратної матриці
Теорема. Визначник добутку двох квадратних матриць
Рівність перевіримо для матриць другого порядку.
Приклад. Перевірити рівність (1) для таких матриць
Розв’язання. Обчислимо спочатку визначники заданих матриць та добуток їх
Знайдемо тепер добуток матриць
Отже,
Приклади. Знайти визначники матриць: 1. 4. Для поданих матриць
Відповіді. 1. -1. 2. 343. 3. 7. 6,-6,-36. 8. -6, -33, 198.
Обернена матриця. Поняття оберненої матриці розглянемо на прикладі квадратної матриці третього порядку, яке по аналогії можна буде узагальнити для матриць довільного порядку. Нехай
Означення 1. Матриця Якщо ж Означення 2. Квадратна матриця
тобто добуток цих матриць дорівнює одиничній матриці Теорема. Якщо матриця Доведемо необхідність. Нехай матриця
Тому рівність (2) можлива тільки тоді, коли Достатність. Нехай визначник матриці Для кожного з елементів
(див., розв’язаний в 1.5 приклад, де отримано матрицю із алгебраїчних доповнень разом з перевіркою вірності їх значень). Протранспонуємо матрицю
За допомогою теорем про розклад та анулювання для визначників третього порядку неважко перевірити, що Приклад 1. Знайти обернену матрицю до матриці
Розв’язання здійснимо у такій послідовності 1) Обчислимо визначник матриці
Оскільки 2)Знаходимо алгебраїчні доповнення елементів матриці
3) Записуємо нову матрицю за формулою (3)
4) За формулою (4) отримуємо обернену матрицю
5) перевіримо, що
Приклад 2. Знайти матрицю, обернену до матриці
Розв’язання. 1) 2)
3) 4) 5)
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1827; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.014 с.) |

 називається прямокутна таблиця, складена із
називається прямокутна таблиця, складена із  чисел вигляду
чисел вигляду  , розміщених в
, розміщених в 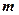 рядках і
рядках і 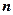 стовпцях, яка позначається
стовпцях, яка позначається
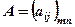 . Зустрічаються також позначення
. Зустрічаються також позначення
 називаються елементами матриці.
називаються елементами матриці.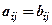 . Позначається
. Позначається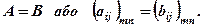
 розміру
розміру 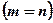 . У цьому випадку говорять, що матриця має порядок
. У цьому випадку говорять, що матриця має порядок  ).
).

 .
.


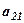
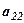

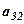
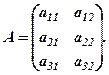
 і
і 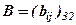 – результати роботи 3-х змін за першу і другу добу відповідно, то можна знайти сумарні результати за дві доби додаванням відповідних елементів і позначити це
– результати роботи 3-х змін за першу і другу добу відповідно, то можна знайти сумарні результати за дві доби додаванням відповідних елементів і позначити це
 на матрицю
на матрицю  розміру
розміру 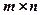 називається нова матриця
називається нова матриця 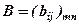 того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці
того ж розміру, кожний елемент якої дорівнює відповідному елементу матриці 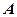 помноженному на число
помноженному на число 
 .
. того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць–доданків, тобто
того ж розміру, кожний елемент якої дорівнює сумі відповідних елементів матриць–доданків, тобто  , і позначається
, і позначається 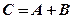 .
. , то
, то  — різниця матриць.
— різниця матриць.
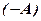 — протилежну матриці
— протилежну матриці 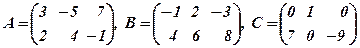
 .
.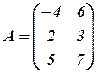 ,
,  .
.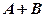 ; 2)
; 2)  .
.
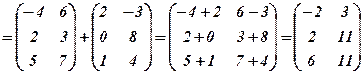 .
.
 .
.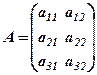
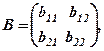
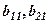 – норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець:
– норми оплати праці робітників: за 1 погонний метр по виїмці породи і за 1 погонний метр по кріпленню відповідно. Другий стовпець:  – відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення.
– відповідні капітальні затрати за 1 погонний метр виїмки і за 1 погонний метр кріплення. сумму грошей зароблену
сумму грошей зароблену  -ю зміною
-ю зміною 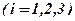 . Аналогічно підраховуються капітальні затрати
. Аналогічно підраховуються капітальні затрати  для
для 
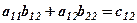
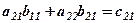


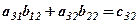
 , що отримана з матриць
, що отримана з матриць 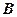 за допомогою операції, яку називають множенням матриць, і позначають
за допомогою операції, яку називають множенням матриць, і позначають
 необхідна їх узгодженність, тобто, щоб число стовпців матриці
необхідна їх узгодженність, тобто, щоб число стовпців матриці  розміру
розміру  , елементи якої
, елементи якої 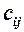 дорівнюють сумі добутків елементів
дорівнюють сумі добутків елементів  -того рядка матриці
-того рядка матриці  -того стовпця матриці
-того стовпця матриці 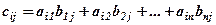 .
.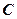 дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника.
дорівнює числу рядків першого співмножника, а число стовпців- числу стовпців другого співмножника. і
і  , якщо
, якщо  ,
,  .
. розміром 2х3, тобто
розміром 2х3, тобто

 .
.
 .
.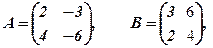

 .
.
 .
.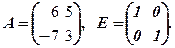
 де
де  .
. , а матриці
, а матриці 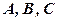 такі:
такі: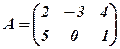 ,
, 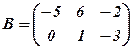 , С=
, С= 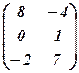 .
.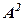 ) називається добуток
) називається добуток  , тобто
, тобто  .
. .
. ,
,  ,
,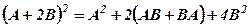 , та знайти значення виразів.
, та знайти значення виразів. - заданий многочлен і
- заданий многочлен і 
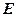 - одинична матриця, називається многочленною матрицею.
- одинична матриця, називається многочленною матрицею.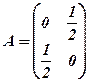
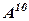
 . 10
. 10  . 11.
. 11.  .
. . 13.
. 13. 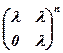 . 14.
. 14. 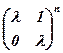 .
.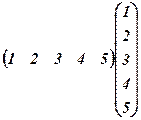 . 16.
. 16.  .
.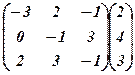 .
. , якщо задана матриця
, якщо задана матриця 
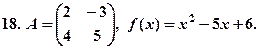
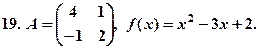
 8.
8. 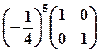 . 9.
. 9.  .
. . 11.
. 11.  . 12.
. 12.  .
. . 14.
. 14. 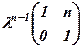 . 15.
. 15. 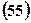 .
. . 17.
. 17.  .
.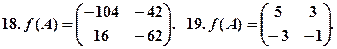
 (скорочення від латинської назви детермінант), або |
(скорочення від латинської назви детермінант), або |  то
то 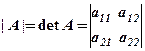 .
. , або
, або 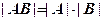 . (1)
. (1)


 ;
; 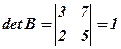 ,
, .
.
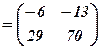 .
.  .
.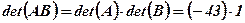 .
. .
.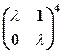 .
.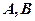 знайти їх добуток
знайти їх добуток  та обчислити визначники. Результат перевірити за допомогою теореми.
та обчислити визначники. Результат перевірити за допомогою теореми.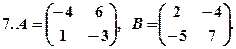

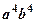 . 4. 1. 5.
. 4. 1. 5.  . 6.
. 6.  .
. .
. .
.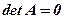 , то матриця називається особливою (виродженою).
, то матриця називається особливою (виродженою). називається оберненою до матри ці
називається оберненою до матри ці  (1)
(1) . За теоремою про визначник добутку двох матриць маємо
. За теоремою про визначник добутку двох матриць маємо , бо
, бо  . (2)
. (2)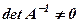 і
і  . Покажемо, як знайти обернену матрицю.
. Покажемо, як знайти обернену матрицю.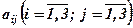 матриці
матриці  :
:  , розмістивши їх у вигляді нової матриці
, розмістивши їх у вигляді нової матриці  відповідно розташуванню елементів
відповідно розташуванню елементів  (3)
(3)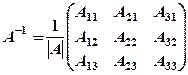 . (4)
. (4)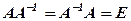 .
.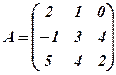 .
. .
.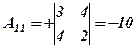 ;
;  ;
; 
 ;
; 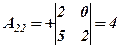 ;
; 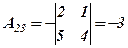 ;
; 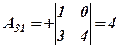 ;
;  ;
;  .
.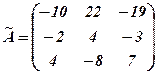 .
. .
.
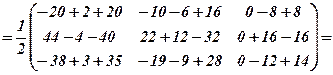

 .
.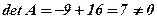 .
. ;
;  ;
; ;
;  .
. .
.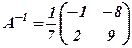 .
.
 .
.


