
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади для самостійного розв’язанняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знайти обернені матриці для матриць: 1. 4. 7. Відповіді: 1. 4. 7.
Розв’язування систем лінійних рівнянь Матричним способом
Обмежимось розглядом системи 3-х лінійних рівнянь
Запишемо такі матриці:
де
Користуючись означенням рівності матриць, ми бачимо, що система ЛР (1) є не що інше, як рівність відповідних елементів матриць – стовпців
Для розв’язання останнього домножимо зліва рівняння (2) на обернену матрицю
Але
Покажемо, що з формули (3) можна отримати формули Крамера. Дійсно, підставляючи в (3) вирази для
За теоремою про заміщення кожний елемент останньої матриці дорівнює значенням допоміжних визначників
Звернемо увагу на те, що в формулі (3) співмножник Приклад 1. Розв’язати систему рівнянь матричним способом
Складемо матрицю системи
Для цієї матриці в 1.12. ми вже знайшли
Тому згідно (3) маємо
Отже, Пропонуємо перевірити відповідь. Приклад 2. Розв’язати матричним способом систему
Розв’язання. Запишемо матриці
У матричному вигляді система запишеться
Визначник матриці
Обернена матриця
Розв’язком системи є матриця
Перевірка:
Зауваження. 1. Розглянутий матричний спосіб на прикладі лінійних систем третього порядку узагальнюється на системи вищих порядків. 2. В більш загальних випадках в матричних рівняннях
матриці 3. При розв’язанні матричних рівнянь вигляду
домножують на обернену матрицю
Приклади для самостійного розв’язання Розв’язати матричним способом системи рівнянь: 1. Розв’язати матричні рівняння 3. 5. 7. Відповіді. 1. 4. Ранг матриці Означення 1. Визначник, складений із елементів матриці Для даної матриці можна складати мінори різних порядків, починаючи від 1 (визначник першого порядку приймається рівним своєму єдиному елементу) до меншого із чисел
Можна скласти 12 мінорів першого порядку (самі елементи), 18 мінорів другого порядку і 4 мінори третього порядку. Випишемо мінори 3-го порядку, знайшовши їх значення (останнє пропонуємо перевірити самостійно)
Серед мінорів другого порядку можуть бути нульові і відмінні від нуля. (Всі їх ми виписувати не будемо). Наприклад, Означення 2. Найвищий порядок мінора матриці Із означення випливає, що якщо ранг матриці Якщо ж матриця нульова, то її ранг дорівнює нулю. Якщо матриця квадратна і невироджена, то її ранг дорівнює порядку матриці. Таким чином, для кожної матриці
В наведеному вище прикладі матриці ми бачили, що найвищий порядок її мінора, відмінного від нуля, дорівнює 2, Знаходження ранга матриці шляхом перебору значень всіх її можливих мінорів пов’язано із значним обсягом обчислень, особливо коли розмір матриці великий. Тому існує простіший спосіб знаходження рангу, заснований на елементарних перетвореннях. До елементарних перетворень матриці відносяться: 1) транспонування матриці; 2)множення елементів рядка (стовпця) матриці на число відмінне від нуля; 3)перестановка місцями двох рядків (стовпців); 4)додавання до елементів одного рядка (стовпця) відповідних елементів другого рядка (стовпця) помножених на одне й те ж саме число.
Теорема. При елементарних перетвореннях ранг матриці не змінюється. Означення 3. Дві матриці Ранги еквівалентних матриць рівні,
Приклад 1. Знайти ранг матриці
Розв’язання. Із другого рядка матриці
Додамо до ІІ-го і ІІІ-го рядків перший, відповідно помножений на –2 і –4, а тоді поміняємо місцями ІІ-ий і ІІІ-ій стовпці, отримаємо:
Помножимо ІІ-ий рядок на –10 і додамо з ІІІ-м рядком:
Матриця Таким чином,
Зауважимо, що ранг матриці можна знаходити, якщо скористатись правилом прямокутника (див. 1.1), яке по суті відповідає послідовному застосуванню елементарних перетворень матриць 1) - 4). Приклад 2. Знайти ранг матриці
Помножимо ІІІ-ій рядок на (-1) і переставимо його з ІІ-м, провідним елементом виберемо
Очевидно що ранг останньої, а значить, і еквівалентної їй початкової матриці А дорівнює 3, тобто Зауваження. При знаходжені рангу матриці великого розміру раціональніше використовувати ЕОМ, застосовуючи відносно простий алгоритм правила прямокутників.
Знайти ранг матриць 1. 3. Відповіді. 1. 2. 2. 2. 3. 3. 4. 3.
1.15.Лінійна залежність та лінійна незалежність рядків (стовпців) матриці
Зупинимось ще на відомому вже в 1.14. прикладі матриці
Там було встановлено, що ранг
Покажемо, що можна знайти числа
Дійсно, підставивши в (1) вирази для
Відомо, що два рядки рівні, якщо в них рівні відповідні елементи, тобто
Із системи (2) знаходимо:
або ще будемо говорити, що рядок Перейдемо до означення понять лінійної залежності і лінійної незалежності рядків (стовпців) матриці Нехай
– рядки матриці
де
Рівність (3) можна переписати у вигляді
де нуль в правій частині означає нульовий рядок. Означення. Рядки
Якщо ж рівність (4) виконується тільки за умови, що всі коефіцієнти Ми вже відмічали, що якщо один з рядків матриці лінійно виражається через інші, то вони лінійно залежні. Навпаки, якщо має місце лінійна залежність (4) і при цьому хоча б один з коефіцієнтів, наприклад,
тобто Аналогічним чином можна ввести поняття лінійної залежності і лінійної незалежності стовпців матриці
Теорема (про лінійну залежність і лінійну незалежність). Якщо ранг матриці
Наслідок 1. Максимальне число лінійно незалежних стовпців матриці дорівнює максимальному числу лінійно незалежних рядків, тому що при транспонуванні матриці її рядки стають стовпцями, а ранг при цьому не міняється.
Наслідок 2. Для того, щоб визначник дорівнював нулю, необхідно і досить, щоб його рядки (стовпці) були лінійно залежними.
1.16. Умови сумісності системи лінійних рівнянь. Теорема Кронекера – Капеллі[3]
Дослідимо в загальному вигляді систему
Розв’язком системи (1) називається сукупність чисел Система вигляду (1) називається сумісною, якщо вона має хоча б один розв’язок. Якщо система (1) не має розв’язку, то вона називається несумісною. Питання сумісності або несумісності системи можна розв’язати за допомогою ранга матриці. Розглянемо матриці:
Матриця Умови сумісності чи несумісності системи лінійних рівнянь (1) виражаються наступною теоремою.
Теорема 1. (Кронекера – Капеллі). Для того щоб система лінійних рівнянь (1) було сумісною, необхідно і досить, щоб ранг матриці системи Із теореми випливає, що якщо Сумісна система може мати єдиний розв’язок і тоді вона називається визначеною, або система може мати нескінченне число розв’язків і тоді вона називається невизначеною. Теорема 2. Сумісна система (1) має єдиний розв’язок, якщо
Вправи. Дослідити кожну із систем рівнянь і у випадку сумісності розв’язати її:
Відповіді: 1. Система несумісна. 2. Система має нескінченне число розв’язків, загальний розв’язок 5. Система має нескінченне число розв’язків, загальний розв’язок:
[1] К..Гаусс(1777-1855)-німецький математик,фізик,астроном [2] Г. Крамер (1704 - 1752) - швейцарський математик. [3] Л. Кронекер (1823 – 1891) – німецький математик, А. Капеллі (1855 – 1910) – італійський математик.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.169 (0.01 с.) |

 . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
.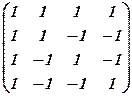 .
.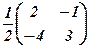 . 2.
. 2. 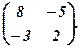 3.
3.  .
. ..5.
..5.  . 6.
. 6. 
 .
.
 ,
,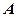 складена з коефіцієнтів при невідомих — матриця системи,
складена з коефіцієнтів при невідомих — матриця системи,  – матриця вільних членів,
– матриця вільних членів,  – матриця невідомих. Знайдемо добуток
– матриця невідомих. Знайдемо добуток
 і
і 
 , вважаючи, що
, вважаючи, що  , отримаємо
, отримаємо
 , а
, а  , тоді розв’язок матричного рівняння (2) запишеться
, тоді розв’язок матричного рівняння (2) запишеться (3)
(3)
 , які були введені при розв’язуванні систем за формулами Крамера. Тому далі маємо
, які були введені при розв’язуванні систем за формулами Крамера. Тому далі маємо
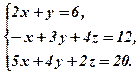

 і обернену матрицю
і обернену матрицю



 ,
,  ,
,  .
. .
. , існує обернена матриця
, існує обернена матриця  ;
;  ;
; ;
; 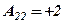 .
. .
.
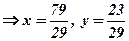 .
. ,
, .
.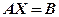

 .
. 2.
2. 
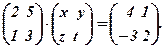 4.
4. 
 . 6.
. 6.  .
.
 . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  .
. , які знаходяться на перетині довільних її
, які знаходяться на перетині довільних її  рядків і
рядків і  або
або  . Так для матриці
. Так для матриці .
.

 .
. , то серед мінорів
, то серед мінорів  -того порядку є відмінні від нуля мінори, а всі мінори
-того порядку є відмінні від нуля мінори, а всі мінори  -го порядку дорівнюють нулю.
-го порядку дорівнюють нулю.
 .
. .
.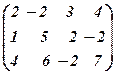 ~
~  .
. ~
~ 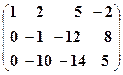 .
.
 .
. .
.


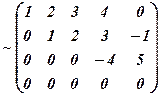 .
. .
. . 2.
. 2.  .
. . 4.
. 4.  .
. .
. . Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці
. Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці 
 і
і  такими, що
такими, що . (1)
. (1) маємо:
маємо:
 (2)
(2) . Таким чином,
. Таким чином, ,
, є лінійною комбінацією рядків
є лінійною комбінацією рядків  або ж рядок
або ж рядок  і
і  .
. в загальній формі.
в загальній формі.

 – деякі числа. Будемо говорити, що
– деякі числа. Будемо говорити, що  , тобто
, тобто рядки цієї матриці, або що
рядки цієї матриці, або що  або ж, що рядок
або ж, що рядок  .
. ,
, матриці
матриці  , не рівні одночасно нулю, що
, не рівні одночасно нулю, що (4)
(4) , то рядки
, то рядки  , то
, то ,
,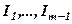 .
.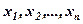 (
( – задані коефіцієнти):
– задані коефіцієнти):
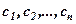 , яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих
, яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих  ,
,  .
. . Відмітимо, що
. Відмітимо, що  , тому що елементи матриці
, тому що елементи матриці  .
. , то система несумісна.
, то система несумісна. (ранги дорівнюють числу невідомих); якщо
(ранги дорівнюють числу невідомих); якщо 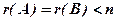 , то система має нескінченне число розв’язків.
, то система має нескінченне число розв’язків.
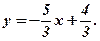 3. (1, 1, 1). 4. Система несумісна.
3. (1, 1, 1). 4. Система несумісна.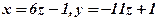 .
.


