
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язання типових задач3Содержание книги Поиск на нашем сайте
Приклади розв’язання типових задач3 Приклад 3 Визначити кількість інтервалів та побудувати інтервальний варіаційний ряд у табличному та графічному вигляді на основі наведеної сукупності ознаки Х: 35, 36, 36, 38, 40, 40, 41, 41, 43, 45, 46, 46, 47, 50, 50, 51, 51, 52, 52, 52, 53, 55, 57, 59, 59, 60, 60, 61, 62, 64, 66, 67, 68, 68, 69, 70, 72, 73, 73, 75, 75, 76, 76, 77, 78. Розв’язання Для визначення кількості інтервалів скористуємося формулою Стерджеса: m = 1 + log 2 n,де n – обсяг сукупності.Оскільки обсяг сукупності n = 45, то перейдемо від логарифму по основі 2 до десяткового логарифму за формулою: logа n = logb n / logb a, абоlog2 n = log10 n / log10 2, враховуючи, що log10 2 = 0,3010, маємоlog2 n = 3,322 log10 n, тоді формула Стерджеса набуває вигляду:m = 1 + 3,322 lg nоді кількість інтервалів: m = 1 + 3,322 × 1,6532 = 6,49 = 6. Оскільки значення ознаки розташовані більш менш рівномірно, використовуємо принцип рівності інтервалів. Ширину кожного інтервалу обчислюємо за формулою:h = (xmax – xmin): m, де xmax – максимальне значення ознаки; xmin – мінімальне значення ознаки m – число інтервалів.h = (78 – 35): 6 = 7,2.Тепер визначаємо межі інтервалів:xmin 1 = xmin = 35.xmax 1 = xmin 2 = xmin 1 + h = 35 + 7,2 = 42,2;xmax 2 = xmin 3 = xmin 2 + h = 42,2 + 7,2 = 49,4;xmax 3 = xmin 4 = xmin 3 + h = 49,4 + 7,2 = 56,6;xmax 4 = xmin 5 = xmin 4 + h = 56,6 + 7,2 = 63,8;xmax 5 = xmin 6 = xmin 5 + h = 63,8 + 7,2 = 71;xmax 6 = xmin 6 + h = 71 + 7,2 = 78,2Створюємо таблицю, яка складається з двох рядків. У верхньому рядку наводимо значення ознаки Х у вигляді визначених інтервалів. Підраховуємо кількість ознак, значення яких потрапляє до відповідного інтервалу, і результати наводимо у нижньому рядку. Отримаємо таку таблицю:
Розподіл значень ознаки Х Висновок: визначивши кількість інтервалів та побудувавши інтервальний варіаційний ряд у табличному та графічному вигляді на основі наведеної сукупності ознаки Х, ми бачимо, що найбільша кількість одиниць сукупності знаходиться в двох інтервалах (49,4 – 56,6) та (71,0 – 78,2) – по 9 одиниць, а найменша - 5 одиниць - у другому інтервалі (42,2 – 49,4). ЪПриклад 4 Дані про розподіл робітників двох підприємств за рівнем заробітної платні наведені у таблиці:
Провести перегрупування робітників за рівнем заробітної платні, утворивши такі групи: до 700; 700 – 1000; 1000 – 1300; 1300 і більше. Розв’язання Перегрупування, або вторинне групування, проводиться за припущенням, що в межах одного інтервалу значення ознак розташовано рівномірно. Це припущення дає право ділити частоту інтервалу на частки, пропорційно відрізкам інтервалу. Так, за умовами вторинного групування слід утворити перший інтервал до 700. Для першого підприємства до новоутвореного інтервалу за даними первинного групування увійде перший інтервал (до 500) та другий інтервал, оскільки 700 становить верхню межу другого інтервалу. Враховуючи припущення, до першого новоутвореного інтервалу ввійде частота першого інтервалу первинного групування та частота другого інтервалу первинного групування. Таким чином, частота першого інтервалу вторинного групування дорівнюватиме 20 + 52 = 72, ми використовуємо тут метод простого укрупнення інтервалу. Другий інтервал вторинного групування включає повністю третій інтервал (700 – 900) та половину четвертого інтервалу первинного групування, так як його верхня межа становить 1000. Відповідно частота другого інтервалу вторинного групування дорівнюватиме 64 +0, 5 × 46 = 87. Тут використовується метод перегрупування за часткою окремих груп в загальному їх підсумку (пропорційний дольовий перерозподіл). Аналогічно проводимо розрахунки для решти інтервалів. Розрахунки наведені у відповідних таблицях. Підприємств
Підприємство ІІ
Висновок: якщо за первинними групуваннями для двох підприємств не можна було робити порівняльний аналіз, то за вторинними групуваннями такий аналіз можливий. Наприклад, можна зробити висновок, що на першому підприємстві значно більша кількість робітників, які отримують найнижчий рівень заробітної плати, а от найвищу заробітну плату на обох підприємствах отримує майже однакова кількість робітників. Тема 5 Приклади розв’язання типових задач Приклад 1 Маємо дані про доходи Зведеного бюджету області, млн. грн., наведені в таблиці. Необхідно визначити показники структури доходної частини бюджету області та оцінити структурні зрушення, що відбулися за цей період. Зробити висновк
Розв’язання: Визначаємо за кожен рік відносні величини структури діленням значень за окремим видом надходжень на їх загальний підсумок. Так, у 2000 році частка податкових надходжень становила 927/1159 = 0,8 або 80,0%; частка неподаткових надходжень - 130/1159 = 0,112 або 11,2%; частка інших надходжень (офіційні трансферти, державні цільові фонди, доходи від операцій з капіталом) – 102/1159 = 0,088 або 8,8%. Результати розрахунків у відсотках наведено у таблиці, де в останніх графах показані структурні зрушення, які визначені як різниця між часткою (у %), що припадала на відповідний вид надходжень у поточному та попередньому роках. Приклад 2 За вихідними даними попереднього прикладу необхідно проаналізувати динаміку доходів Зведеного бюджету області, визначивши відносні величини динаміки. Зробити висновки. Приклад 6 Кількість зареєстрованих розлучень за чотири роки зросла у 1,57 рази, у тому числі: за перший рік – у 1,08; за другий – у 1,1; за третій – у 1,18; за четвертий – у 1,12рази. Розрахувати середньорічний темп зростання кількості зареєстрованих розлучень. Розв’язання: Дані не згруповані, осереднювана ознака представлена відносними величинами динаміки, тому середню величину розраховуємо як середню геометричну просту:
тобто, в середньому за рік кількість зареєстрованих розлучень зростала в 1,119 рази або на 11,9%. Приклад 3 Визначити кількість інтервалів та побудувати інтервальний варіаційний ряд у табличному та графічному вигляді на основі наведеної сукупності ознаки Х: 35, 36, 36, 38, 40, 40, 41, 41, 43, 45, 46, 46, 47, 50, 50, 51, 51, 52, 52, 52, 53, 55, 57, 59, 59, 60, 60, 61, 62, 64, 66, 67, 68, 68, 69, 70, 72, 73, 73, 75, 75, 76, 76, 77, 78 Розв’язання Для визначення кількості інтервалів скористуємося формулою Стерджеса: m = 1 + log 2 n,де n – обсяг сукупності.Оскільки обсяг сукупності n = 45, то перейдемо від логарифму по основі 2 до десяткового логарифму за формулою: logа n = logb n / logb a, абоlog2 n = log10 n / log10 2, враховуючи, що log10 2 = 0,3010, маємоlog2 n = 3,322 log10 n, тоді формула Стерджеса набуває вигляду: m = 1 + 3,322 lg nТоді кількість інтервалів: m = 1 + 3,322 × 1,6532 = 6,49 = 6. Оскільки значення ознаки розташовані більш менш рівномірно, використовуємо принцип рівності інтервалів. Ширину кожного інтервалу обчислюємо за формулою:h = (xmax – xmin): m, де xmax – максимальне значення ознаки;xmin – мінімальне значення ознаки; m – число інтервалівh = (78 – 35): 6 = 7,2. Тепер визначаємо межі інтервалів:xmin 1 = xmin = 35.xmax 1 = xmin 2 = xmin 1 + h = 35 + 7,2 = 42,2;xmax 2 = xmin 3 = xmin 2 + h = 42,2 + 7,2 = 49,4;xmax 3 = xmin 4 = xmin 3 + h = 49,4 + 7,2 = 56,6;xmax 4 = xmin 5 = xmin 4 + h = 56,6 + 7,2 = 63,8;xmax 5 = xmin 6 = xmin 5 + h = 63,8 + 7,2 = 71;xmax 6 = xmin 6 + h = 71 + 7,2 = 78,2 Створюємо таблицю, яка складається з двох рядків. У верхньому рядку наводимо значення ознаки Х у вигляді визначених інтервалів. Підраховуємо кількість ознак, значення яких потрапляє до відповідного інтервалу, і результати наводимо у нижньому рядку. Отримаємо таку таблицю:
Висновок: визначивши кількість інтервалів та побудувавши інтервальний варіаційний ряд у табличному та графічному вигляді на основі наведеної сукупності ознаки Х, ми бачимо, що найбільша кількість одиниць сукупності знаходиться в двох інтервалах (49,4 – 56,6) та (71,0 – 78,2) – по 9 одиниць, а найменша - 5 одиниць - у другому інтервалі (42,2 – 49,4). Приклад 4 Дані про розподіл робітників двох підприємств за рівнем заробітної платні наведені у таблиці:
Провести перегрупування робітників за рівнем заробітної платні, утворивши такі групи: до 700; 700 – 1000; 1000 – 1300; 1300 і більше. Розв’язання Перегрупування, або вторинне групування, проводиться за припущенням, що в межах одного інтервалу значення ознак розташовано рівномірно. Це припущення дає право ділити частоту інтервалу на частки, пропорційно відрізкам інтервалу.Так, за умовами вторинного групування слід утворити перший інтервал до 700. Для першого підприємства до новоутвореного інтервалу за даними первинного групування увійде перший інтервал (до 500) та другий інтервал, оскільки 700 становить верхню межу другого інтервалу. Враховуючи припущення, до першого новоутвореного інтервалу ввійде частота першого інтервалу первинного групування та частота другого інтервалу первинного групування. Таким чином, частота першого інтервалу вторинного групування дорівнюватиме 20 + 52 = 72, ми використовуємо тут метод простого укрупнення інтервалу. Другий інтервал вторинного групування включає повністю третій інтервал (700 – 900) та половину четвертого інтервалу первинного групування, так як його верхня межа становить 1000. Відповідно частота другого інтервалу вторинного групування дорівнюватиме 64 +0, 5 × 46 = 87. Тут використовується метод перегрупування за часткою окремих груп в загальному їх підсумку (пропорційний дольовий перерозподіл). Аналогічно проводимо розрахунки для решти інтервалів. Розрахунки наведені у відповідних таблицях Підприємство І
Підприємство ІІ
Висновок: якщо за первинними групуваннями для двох підприємств не можна було робити порівняльний аналіз, то за вторинними групуваннями такий аналіз можливий. Наприклад, можна зробити висновок, що на першому підприємстві значно більша кількість робітників, які отримують найнижчий рівень заробітної плати, а от найвищу заробітну плату на обох підприємствах отримує майже однакова кількість робітників.
Приклад 1 Проаналізувати структурні зміни за наведеними даними (дані умовні) про розподіл споживчих витрат населення регіону за окремі періоди і в цілому за весь час:Структура споживчих витрат населення регіону
Розв’язання: Зміну структури споживчих витрат населення регіону можна дослідити за допомогою лінійного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.3), квадратичного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.4), квадратичного коефіцієнта відносних структурних зрушень (формула 4.7.5) та лінійного коефіцієнта “абсолютних” структурних зрушень за n періодів (формула 4.7.6). Для визначення цих показників зробимо допоміжні розрахунки у табличній формі (див. наступну сторінку). Для розрахунку лінійного коефіцієнта “абсолютних” структурних зрушень (формула 4.7.3) за перший (із 2004 по 2005 рік) і за другий (із 2005 по 2006 рік) періоди використовуємо підсумки стовпчиків 2 і 5 розрахункової таблиці:
За наступний рік “абсолютні” структурні зрушення зменшилися, тобто структура споживчих витрат почала стабілізуватися. Аналогічних висновків можна дійти і за розрахунком квадратичного коефіцієнта “абсолютних” структурних зрушень (розрахунки за формулою 4.7.4 із використанням підсумків стовпчиків 3 і 6 розрахункової таблиці):
Визначимо величину квадратичного коефіцієнта відносних структурних зрушень (формула 4.7.5), використовуючи підсумки стовпчиків 4 і 7 розрахункової таблиці:
Для узагальнюючої оцінки структурних зрушень у досліджуваній сукупності в цілому за весь час використовуємо лінійний коефіцієнт “абсолютних” структурних зрушень за n періодів (формула 4.7.6 із підсумками з стовпчика 8 розрахункової таблиці).
Приклад 2 Провести порівняльний аналізи динаміки заощаджень населення в двох регіонах країни за умовними даними, наведеними в таблиці:
Розв’язання: При необхідності порівняння характеристик паралельних рядів динаміки явищ, що одночасно розвиваються у часі, попередньо проводять приведення їх до однієї основи, для чого переводять абсолютні показники рівнів кожного ряду у відносні, прийнявши рівень якогось одного періоду за одиницю або за сто (за суттю при цьому розраховуються для кожного ряду базисні коефіцієнти або темпи росту). Представимо результати розрахунку в таблиці. (Для регіону Б зроблені аналогічні розрахунки).
Отримані значення темпів росту свідчать про те, що при взятому за основу рівні 2001 року темпи зростання грошових заощаджень значно вищі в регіоні Б, ніж у регіоні А. Але не завжди результати такі очевидні. Порівняльний аналіз в цілому за весь період часу можна зробити, визначивши середньо річні темпи зростання або приросту по кожному регіону і порівнявши їх, тобто визначити коефіцієнт випередження. Визначаємо для кожного регіону середньо річні темпи зростання, використовуючи формули 4.8.14 і 4.8.15 : регіон А - аналогічний розрахунок виконуємо для регіону Б
В середньому за рік у регіоні А грошові заощадження населення зростали на 2,4 %, а у регіоні Б – на 4,1 %. Розраховуємо коефіцієнт випередження, як співвідношення темпів приросту (або темпів росту)
Тема 9 Приклади розв’язання типових задач Приклад 1 Динаміка виробництва продукції на підприємстві характеризується умовними даними, наведеними в таблиці.
Визначити тенденцію розвитку та встановити її характер, використавши різні методи. Зробити висновки та прогнозні розрахунки на кінець року. Розв’язання Приклад 2 Маємо дані про продаж товарів у приватному торгівельному підприємстві.
Обчисліть: 1) загальні індекси товарообігу, цін і фізичного обсягу реалізації товарів; 2) зміни обсягу товарообігу в абсолютному виразі в цілому та під впливом зміни рівня окремих чинників. Розв'язання: Загальні індекси щодо 3-х товарів разом за формою будуть агрегатними, оскільки реалізовані товари є різними. Індекс товарообігу буде дорівнювати: Ірq = Σ р1q1: Σ р0q0 = (64 + 44 + 38): (60 + 42 + 35) = 146: 137 = = 1,066 (106,6% або +6,6%). Отже, у цілому товарообіг збільшився на 6,6 %. В абсолютному виразі цей приріст становитиме Δ pq = Σ р1q1 - Σ р0q0 = 146 - 137 = + 9,0 тис. грн. Індекс цін визначаємо як середньозважений гармонійний, для чого зміну середніх цін у 2-му кварталі порівняно з 1-м у % представимо у вигляді коефіцієнтів, тобто індивідуальних індексів ціни на окремі товари: ip 1=(-20+100):100= 0,8; ip 2=(+10+100):100= 1,1; ip 3=(0+100):100= 1,0; Ір = Σ р1q1: Σ р0q1 = = 146: 158 = 0,924 (92,4 % або - 7,6%). Отже, під впливом зниження цін товарообіг зменшився на 7,6 %. В абсолютному виразі це зменшення становитиме:
Δ pq (p) = Σ р1q1 - Σ р0q1 = 146 - 158 = - 12,0 тис. грн.
Індекс фізичного обсягу реалізації товарів буде дорівнювати Іq = Σ р0 q1: Σ р0 q0 = 158: 137 = 1,153, (115,3 % або + 15,3%).
Отже, під впливом зростання фізичного обсягу реалізації товарів товарообіг збільшився на 15,3 %. В абсолютному виразі цей приріст становитиме Δ pq (q) = Σ р0 q1 - Σ р0 q0 = 158 - 137 = +21,0 тис. грн. Перевірка: 1) Взаємозв'язок індексів: 1,066 = 0,924 . 1,154; 2) зв'язок абсолютних приростів: + 9 = - 12 + 21 тис. грн. Приклад 3 Маємо дані про діяльність відділень банку, представлені в таблиці (тис. грн.).
На основі наведених в таблиці даних розрахувати: А. загальні індекси кредитового обороту, швидкості обороту позик та середніх залишків позик. Б. абсолютний приріст кредитового обороту в цілому та за рахунок окремих чинників. Зробити висновки. Розв’язання завдання А: Швидкість обороту позик визначається як співвідношення кредитового обороту (КО) до середніх залишків позик:Ш = Загальний індекс кредитового обороту визначаємо за формулою:
Загальний індекс швидкості обороту позик
Загальний індекс середніх залишків позик
Перевіримо взаємозв’язок між розрахованими індексами
Отримані результати свідчать про те, що в цілому кредитовий оборот у двох відділеннях банку зріс у 1,076 рази, або на 7,6 %. Це відбулося за рахунок зростання швидкості обороту позик (+ 19,3%), та за рахунок зниження середніх залишків позик (– 9,8%). Розв’язання завдання Б: Визначимо абсолютний приріст кредитового обороту в цілому та за рахунок окремих чинників Δ КО = Σ КО1 – Σ КО0 = Σ Ш1З1 - Σ Ш0З0 = 990 – 920 = +70 тис. грн.; Δ КО(Ш) = (Σ Ш1З1 – Σ Ш0З1 ) = 990 – 830 = +160 тис. грн.; Δ КО(З ) = (Σ Ш0З1 – Σ Ш0З0) = 830 - 920 = - 90 тис. грн. Таким чином, кредитовий оборот в цілому зріс на 70 тис. грн., в тому числі за рахунок прискорення швидкості обертання позик він зріс на 160 тис. грн., а за рахунок зміни середніх залишок позик - зменшився на 90 тис. грн. Перевірка взаємозв’язку між абсолютними приростами Δ КО = Δ КО(Ш) + Δ КО(З ) = 160 – 90 = 70 тис.грн. Приклад 4 Маємо дані про діяльність відділень банку, представлені в таблиці (тис. грн.).
На основі наведених в таблиці даних оцінити динаміку середньої швидкості обороту позик, розрахувавши індекси середньої швидкості обороту позик змінного, фіксованого складу та індекс структурних зрушень. Зробити висновки. Розв’язання: Осереднюється швидкість обороту позик (якісний показник), тому середні залишки позик – показник, який знаходиться у знаменнику логічної формули визначення Ш, є показником - сумірником, тобто вагами. Будуємо систему взаємопов’язаних зведених індексів, що характеризують динаміку середньої швидкості обороту позик. Індекс середньої швидкості обороту позик змінного складу визначаємо за формулою 4.10.14:
Індекс середньої швидкості обороту позик фіксованого складу визначаємо за формулою 4.10.15:
Визначені індекси свідчать про те, що середня швидкість оборотупозик у звітному періоді порівняно із базовим зросла в цілому на 19,1%. При цьому, за рахунок зростання швидкості обороту позик середня швидкість оборотупозик зросла на 19,3%, а за рахунок змін у структурі залишків позик вона знизилася на 0,1%.
Приклад 1 На основі даних, наведених у табл. встановити наявність кореляційного зв’язку, визначити лінію регресії за лінійною моделлю. Оцінити істотність і щільність зв’язку. Приклад 2 Дані про споживання м’яса в сім’ях робітників та службовців з різним рівнем середньодушового сукупного доходу наведено у таблиці:
Встановити взаємозв’язок та оцінити його істотність і щільність за допомогою методу аналітичного групування. Розв’язання: Розрахуємо середні величини в кожній групі за формулою середньої арифметичної простої:
Тоді:
Середню з групових дисперсій розрахуємо за формулою: Міжгрупову дисперсію обчислимо за формулою:
Обчислимо кореляційне відношення: Критичне значення кореляційного відношення для обсягу сукупності 20 одиниць та трьох груп дорівнює 0,318. Відповідь: Оскільки розраховане кореляційне відношення більше за його критичне значення, між рівнем середньодушового доходу та споживанням м’яса існує прямий щільний зв’язок.
Тема 12Приклади розв’язання типових зада Приклад 1 Під час безповторного вибіркового спостереження, яке проводилось в одній з крамниць продажу дешевого одягу були отримані такі дані:Розподіл проданого товару за цінами
Визначити середню ціну та граничну помилку з імовірністю 0,954; побудувати довірчий інтервал для середньої ціни. Загальна кількість товарів (обсяг генеральної сукупності) 3254 одиниць. Розв’язання: Для розрахунку середньої ціни за одиницю проданого товару замінимо спочатку інтервальний ряд розподілу дискретним. Використовуючи прийняте у статистиці припущення, що в межах одного інтервалу розподіл уважається рівномірним, значення ознаки (у даному прикладі ціна на товар) замінюємо на відповідні середні значення, які розраховуються за формулою: Маємо такі значення:
З урахуванням обчислених значень середин інтервалів, вихідні дані набувають такого вигляду: Дискретний ряд розподілу проданого товару за цінами
Середня ціна обчислюється за формулою середньої арифметичної зваженої:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.198 (0.012 с.) |

 =15+ + 25 +16 = 56
=15+ + 25 +16 = 56

 ,
, проц. пункти;
проц. пункти;  проц. пункти.Таким чином, із 2004 по 2005 рік питома вага окремих видів споживчих витрат населення в середньому змінювалася на 5,6 проц. пункти.
проц. пункти.Таким чином, із 2004 по 2005 рік питома вага окремих видів споживчих витрат населення в середньому змінювалася на 5,6 проц. пункти. проц. пункти;
проц. пункти;  проц. пункти.
проц. пункти. ;
;  .Як свідчать ці розрахунки, за перший рік питома вага кожного виду витрат в середньому змінилася майже на ¼ своєї величини, тоді як за наступний рік – тільки на 1/9.
.Як свідчать ці розрахунки, за перший рік питома вага кожного виду витрат в середньому змінилася майже на ¼ своєї величини, тоді як за наступний рік – тільки на 1/9.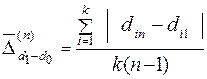 =
=  3,1 проц. пункти.Таким чином, за весь час середньорічна зміна частки споживчих витрат населення регіону за всіма видами витрат становила 3,1 процентних пункти.
3,1 проц. пункти.Таким чином, за весь час середньорічна зміна частки споживчих витрат населення регіону за всіма видами витрат становила 3,1 процентних пункти.
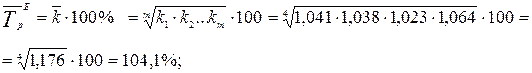
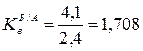 .Таким чином, грошові заощадження населення за період із 2001 по 2006 р. у регіоні Б порівняно із регіоном А зросли у 1,708 рази.
.Таким чином, грошові заощадження населення за період із 2001 по 2006 р. у регіоні Б порівняно із регіоном А зросли у 1,708 рази. = (64 + 44 + 38): (64 / 0,8 + 44 / 1,1 + 38 / 1,0) =
= (64 + 44 + 38): (64 / 0,8 + 44 / 1,1 + 38 / 1,0) = .Швидкість обороту позик це якісний показник, а середні залишки позик – кількісний. Будуємо систему взаємопов’язаних зведених індексів.
.Швидкість обороту позик це якісний показник, а середні залишки позик – кількісний. Будуємо систему взаємопов’язаних зведених індексів.

 (- 9,8%).
(- 9,8%).

 Індекс структурних зрушень визначаємо за формулою 4.10.16:
Індекс структурних зрушень визначаємо за формулою 4.10.16:
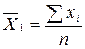 = (48 + 62 + 40 + 52 + 50 + 36) / 6 = 48;
= (48 + 62 + 40 + 52 + 50 + 36) / 6 = 48; 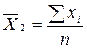 = (91 + 96 + 84 + 95 + 98 + 94 + 92 + 89 + 98 + 92) / 10 = 84,6;
= (91 + 96 + 84 + 95 + 98 + 94 + 92 + 89 + 98 + 92) / 10 = 84,6;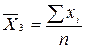 = (100 + 112 + 108 + 110) / 4 = 107,5. Загальну середню для всієї сукупності обчислимо за формулою середньої арифметичної зваженої, де в якості окремих ознак беруться середні кожної групи, а частотами є обсяги відповідних груп:
= (100 + 112 + 108 + 110) / 4 = 107,5. Загальну середню для всієї сукупності обчислимо за формулою середньої арифметичної зваженої, де в якості окремих ознак беруться середні кожної групи, а частотами є обсяги відповідних груп: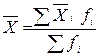 = (48 × 6 + 84,6 × 10 + 107,5 × 4) / 20 = 78,2. Визначаємо групові дисперсії за формулою:
= (48 × 6 + 84,6 × 10 + 107,5 × 4) / 20 = 78,2. Визначаємо групові дисперсії за формулою: 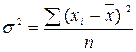 .
.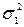 = [(48 – 48)2 + (62 – 48)2 + (40 – 48)2 + (52 – 48)2 + (50 – 48)2 ++ (36 – 48)2 ] / 6 ≈ 70,67;
= [(48 – 48)2 + (62 – 48)2 + (40 – 48)2 + (52 – 48)2 + (50 – 48)2 ++ (36 – 48)2 ] / 6 ≈ 70,67;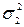 = [(91 – 84,6)2 + (96 – 84,6)2 + (84 – 84,6)2 + (95 – 84,6)2 + (98 – 84,6)2 ++ (94 – 84,6)2 + (92 – 84,6)2 + (89 – 84,6)2 + (98 – 84,6)2 + (92 – 84,6)2 ] / 10 = 85,58;
= [(91 – 84,6)2 + (96 – 84,6)2 + (84 – 84,6)2 + (95 – 84,6)2 + (98 – 84,6)2 ++ (94 – 84,6)2 + (92 – 84,6)2 + (89 – 84,6)2 + (98 – 84,6)2 + (92 – 84,6)2 ] / 10 = 85,58;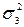 = [(100 – 107,5)2 + (112 – 107,5)2 + (108 – 107,5)2 + (110 – 107,5)2] / 4 = = 20,75.
= [(100 – 107,5)2 + (112 – 107,5)2 + (108 – 107,5)2 + (110 – 107,5)2] / 4 = = 20,75.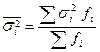 = (70,67 × 6 + 85,58 × 10 + 20,75 × 4) / 20 = 68,14.
= (70,67 × 6 + 85,58 × 10 + 20,75 × 4) / 20 = 68,14.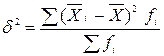
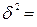 [(48 – 78,2)2 × 6 + (84,6 – 78,2)2 ×10 + (107,5 – 78,2)2 × 4] / 20 = 465,79. Використовуючи правило складання дисперсій
[(48 – 78,2)2 × 6 + (84,6 – 78,2)2 ×10 + (107,5 – 78,2)2 × 4] / 20 = 465,79. Використовуючи правило складання дисперсій 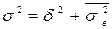 , визначимо загальну дисперсію:
, визначимо загальну дисперсію: 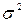 = 465,79 + 68,14 = 533,93.
= 465,79 + 68,14 = 533,93.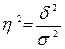 = 465,79 / 533,93 = 0,872.
= 465,79 / 533,93 = 0,872.
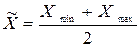 ,де
,де 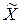 – середина інтервалу;Хmin – нижня межа певного інтервалу;Хmax – верхня межа певного інтервалу.
– середина інтервалу;Хmin – нижня межа певного інтервалу;Хmax – верхня межа певного інтервалу.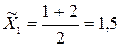 ;
; 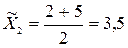 ;
; 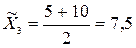 ;
; 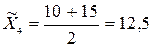 .
.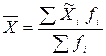 .Тоді середня ціна за даними вибіркового спостереження:
.Тоді середня ціна за даними вибіркового спостереження: 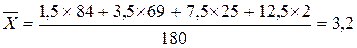 грн.Гранична помилка для безповторного випадкового відбору розраховується за формулою:
грн.Гранична помилка для безповторного випадкового відбору розраховується за формулою: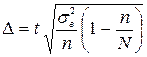 ,де t – довірче число (або квантиль розподілу), яке для великої за обсягом вибірки (більше 30 одиниць) для ймовірності 0,954 дорівнює 2;
,де t – довірче число (або квантиль розподілу), яке для великої за обсягом вибірки (більше 30 одиниць) для ймовірності 0,954 дорівнює 2; 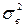 – дисперсія вибірки;n – обсяг вибірки;N – обсяг генеральної сукупності.Дисперсія вибірки обчислюється за формулою:
– дисперсія вибірки;n – обсяг вибірки;N – обсяг генеральної сукупності.Дисперсія вибірки обчислюється за формулою: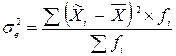 ,де
,де 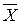 – середня арифметична (середня ціна)fi – частота (кількість проданого товару) кожного окремого інтервалу.Таким чином, дисперсія вибірки:
– середня арифметична (середня ціна)fi – частота (кількість проданого товару) кожного окремого інтервалу.Таким чином, дисперсія вибірки: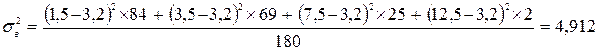 .Тепер можна визначити граничну помилку:
.Тепер можна визначити граничну помилку: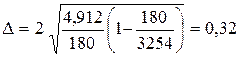 .Таким чином,
.Таким чином, 


