
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод середньої ступінчастоїСодержание книги Поиск на нашем сайте
Об’єднуємо по три інтервали і в кожному укрупненому інтервалі обчислюємо середнє значення рівня динамічного ряду, таким чином, маємо: За результатами згладжування методом середньої ступінчастої бачимо тенденцію до зростання. Визначимо характер тенденції, розрахувавши абсолютні ланцюгові прирости: D 1 = Висновок: абсолютний приріст зростає, тому для даного динамічного ряду маємо тенденцію до прискореного зростання. 2. Метод середньої плинної Об’єднуємо перші три інтервали, обчислюємо середнє значення рівня динамічного ряду, переміщуємося на один інтервал і повторюємо процедуру до кінця динамічного ряду, таким чином, маємо:
Повторне згладжування показало наявність чіткої тенденції до зростання. Визначимо характер тенденції, розрахувавши абсолютні ланцюгові прирости: D 1 = 3. Метод аналітичного вирівнювання а) за лінійною моделлю Лінійна модель має вигляд:
Для спрощення розрахунків складемо допоміжну таблицю: Допоміжна таблиця для розрахунку параметрів лінійної моделі
Тоді: а1 = (9 · 593,8 – 116,5 · 45) / (9 · 285 – 45 · 45) = 0,188;
а0 = 116,5 / 9 – 0,188 · (45 / 9) = 12. Таким чином, лінійна модель має вигляд: уt = 12 + 0,188 t. Для того, щоб визначити виробництво продукції на кінець року, до одержаної моделі замість t підставляємо значення t = 12, тоді: У 12 = 12 + 0,188 t = 12 + 0,188 · 12 = 14,3. б) модель квадратичної параболи Параметри параболи другого порядку:
Y = a + b·t + c·t 2, обчислюють за допомогою системи нормальних рівнянь:
Значення параметра t у разі введення умовного нуля для непарної кількості рівнів динамічного ряду
При цьому å t = 0 та å t3 = 0; а система рівнянь набуває вигляду:
Для спрощення розрахунків складемо допоміжну таблицю: Допоміжна таблиця для розрахунку параметрів моделі
Тоді: b = 11,3 / 60 = 0,188; с = (9 · 779,9 – 116,5 · 60) / (9 · 708 – 60 · 60) = 0,01 а = 116,5 / 9 – 0,01 · (60 / 9) = 12,87 Таким чином, модель квадратичної параболи має вигляд: у = 12,87 + 0,188 t + 0,01 t2. Для того, щоб визначити виробництво продукції на кінець року, до одержаної моделі замість t підставляємо значення t = 12, тоді: y12 = 12,87 + 0,188 t + 0,01 t2 = 12,87 + 0,188 · 12 + 0,01 · 144 = 16,57. Тема 10 Приклади розв’язання типових задач Приклад 2 Маємо дані про продаж товарів у приватному торгівельному підприємстві.
Обчисліть: 1) загальні індекси товарообігу, цін і фізичного обсягу реалізації товарів; 2) зміни обсягу товарообігу в абсолютному виразі в цілому та під впливом зміни рівня окремих чинників.
Розв'язання: Загальні індекси щодо 3-х товарів разом за формою будуть агрегатними, оскільки реалізовані товари є різними. Індекс товарообігу буде дорівнювати: Ірq = Σ р1q1: Σ р0q0 = (64 + 44 + 38): (60 + 42 + 35) = 146: 137 = = 1,066 (106,6% або +6,6%). Отже, у цілому товарообіг збільшився на 6,6 %. В абсолютному виразі цей приріст становитиме Δ pq = Σ р1q1 - Σ р0q0 = 146 - 137 = + 9,0 тис. грн. Індекс цін визначаємо як середньозважений гармонійний, для чого зміну середніх цін у 2-му кварталі порівняно з 1-м у % представимо у вигляді коефіцієнтів, тобто індивідуальних індексів ціни на окремі товари: ip 1=(-20+100):100= 0,8; ip 2=(+10+100):100= 1,1; ip 3=(0+100):100= 1,0; Ір = Σ р1q1: Σ р0q1 = = 146: 158 = 0,924 (92,4 % або - 7,6%). Отже, під впливом зниження цін товарообіг зменшився на 7,6 %. В абсолютному виразі це зменшення становитиме:
Δ pq (p) = Σ р1q1 - Σ р0q1 = 146 - 158 = - 12,0 тис. грн.
Індекс фізичного обсягу реалізації товарів буде дорівнювати Іq = Σ р0 q1: Σ р0 q0 = 158: 137 = 1,153, (115,3 % або + 15,3%).
Отже, під впливом зростання фізичного обсягу реалізації товарів товарообіг збільшився на 15,3 %. В абсолютному виразі цей приріст становитиме Δ pq (q) = Σ р0 q1 - Σ р0 q0 = 158 - 137 = +21,0 тис. грн. Перевірка: 1) Взаємозв'язок індексів: 1,066 = 0,924 . 1,154; 2) зв'язок абсолютних приростів: + 9 = - 12 + 21 тис. грн. Приклад 3 Маємо дані про діяльність відділень банку, представлені в таблиці (тис. грн.).
На основі наведених в таблиці даних розрахувати: А. загальні індекси кредитового обороту, швидкості обороту позик та середніх залишків позик. Б. абсолютний приріст кредитового обороту в цілому та за рахунок окремих чинників. Зробити висновки. Розв’язання завдання А: Швидкість обороту позик визначається як співвідношення кредитового обороту (КО) до середніх залишків позик:Ш = Загальний індекс кредитового обороту визначаємо за формулою:
Загальний індекс швидкості обороту позик
Загальний індекс середніх залишків позик
Перевіримо взаємозв’язок між розрахованими індексами
Отримані результати свідчать про те, що в цілому кредитовий оборот у двох відділеннях банку зріс у 1,076 рази, або на 7,6 %. Це відбулося за рахунок зростання швидкості обороту позик (+ 19,3%), та за рахунок зниження середніх залишків позик (– 9,8%). Розв’язання завдання Б: Визначимо абсолютний приріст кредитового обороту в цілому та за рахунок окремих чинників Δ КО = Σ КО1 – Σ КО0 = Σ Ш1З1 - Σ Ш0З0 = 990 – 920 = +70 тис. грн.; Δ КО(Ш) = (Σ Ш1З1 – Σ Ш0З1 ) = 990 – 830 = +160 тис. грн.; Δ КО(З ) = (Σ Ш0З1 – Σ Ш0З0) = 830 - 920 = - 90 тис. грн. Таким чином, кредитовий оборот в цілому зріс на 70 тис. грн., в тому числі за рахунок прискорення швидкості обертання позик він зріс на 160 тис. грн., а за рахунок зміни середніх залишок позик - зменшився на 90 тис. грн. Перевірка взаємозв’язку між абсолютними приростами
Δ КО = Δ КО(Ш) + Δ КО(З ) = 160 – 90 = 70 тис.грн. Приклад 4 Маємо дані про діяльність відділень банку, представлені в таблиці (тис. грн.).
На основі наведених в таблиці даних оцінити динаміку середньої швидкості обороту позик, розрахувавши індекси середньої швидкості обороту позик змінного, фіксованого складу та індекс структурних зрушень. Зробити висновки. Розв’язання: Осереднюється швидкість обороту позик (якісний показник), тому середні залишки позик – показник, який знаходиться у знаменнику логічної формули визначення Ш, є показником - сумірником, тобто вагами. Будуємо систему взаємопов’язаних зведених індексів, що характеризують динаміку середньої швидкості обороту позик. Індекс середньої швидкості обороту позик змінного складу визначаємо за формулою 4.10.14:
Індекс середньої швидкості обороту позик фіксованого складу визначаємо за формулою 4.10.15:
Визначені індекси свідчать про те, що середня швидкість оборотупозик у звітному періоді порівняно із базовим зросла в цілому на 19,1%. При цьому, за рахунок зростання швидкості обороту позик середня швидкість оборотупозик зросла на 19,3%, а за рахунок змін у структурі залишків позик вона знизилася на 0,1%.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.57.25 (0.013 с.) |

 = (12,3 + 12,5 + 12,2) / 3 = 12,33;
= (12,3 + 12,5 + 12,2) / 3 = 12,33;  = (12,9 + 13,1 + 12,8) / 3 = 12,93;
= (12,9 + 13,1 + 12,8) / 3 = 12,93;  = (13,5 + 13,3 + 13,9) / 3 = 13,57.
= (13,5 + 13,3 + 13,9) / 3 = 13,57. = (12,9 + 13,1 + 12,8) / 3 = 12,93;
= (12,9 + 13,1 + 12,8) / 3 = 12,93;  = (13,1 + 12,8 + 13,5) / 3 = 13,13;
= (13,1 + 12,8 + 13,5) / 3 = 13,13;  = (12,8 + 13,5 + 13,3) / 3 = 13,2;
= (12,8 + 13,5 + 13,3) / 3 = 13,2;  = (13,5 + 13,3 + 13,9) / 3 = 13,57. Оскільки чіткої тенденції розвитку не спостерігається, проводимо повторне згладжування, для чого укрупнюємо інтервали первинного динамічного ряду по п’ять інтервалів, тоді:
= (13,5 + 13,3 + 13,9) / 3 = 13,57. Оскільки чіткої тенденції розвитку не спостерігається, проводимо повторне згладжування, для чого укрупнюємо інтервали первинного динамічного ряду по п’ять інтервалів, тоді: 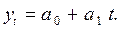 Параметри
Параметри  та
та  згідно з методом найменших квадратів знаходяться розв’язанням системи нормальних рівнянь:
згідно з методом найменших квадратів знаходяться розв’язанням системи нормальних рівнянь: 
 , де n – обсяг сукупності (кількість значень рівнів ряду);y – фактичні рівні ряду;t – порядковий номер періоду або моменту часу;Розв’язавши цю систему, отримуємо значення параметрів лінійної моделі:
, де n – обсяг сукупності (кількість значень рівнів ряду);y – фактичні рівні ряду;t – порядковий номер періоду або моменту часу;Розв’язавши цю систему, отримуємо значення параметрів лінійної моделі: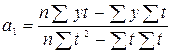 ,
,  , де
, де 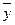 – середній рівень динамічного ряду.
– середній рівень динамічного ряду. . Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t = 0) обрати центральний інтервал. Умовні періоди, розташовані ліворуч умовного нуля, набувають від’ємних значень, а ті, що розташовані праворуч – додатних.
. Розрахунок параметрів значно спрощується, якщо за початок відліку часу (t = 0) обрати центральний інтервал. Умовні періоди, розташовані ліворуч умовного нуля, набувають від’ємних значень, а ті, що розташовані праворуч – додатних. Тоді:
Тоді: 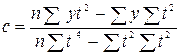 ,
,  ,
,  .
. = (64 + 44 + 38): (64 / 0,8 + 44 / 1,1 + 38 / 1,0) =
= (64 + 44 + 38): (64 / 0,8 + 44 / 1,1 + 38 / 1,0) = .Швидкість обороту позик це якісний показник, а середні залишки позик – кількісний. Будуємо систему взаємопов’язаних зведених індексів.
.Швидкість обороту позик це якісний показник, а середні залишки позик – кількісний. Будуємо систему взаємопов’язаних зведених індексів.

 (- 9,8%).
(- 9,8%).

 Індекс структурних зрушень визначаємо за формулою 4.10.16:
Індекс структурних зрушень визначаємо за формулою 4.10.16:



